镜之国的爱丽丝
0%

00 - 问题解决方案 - 平面

发表于 更新于 分类于

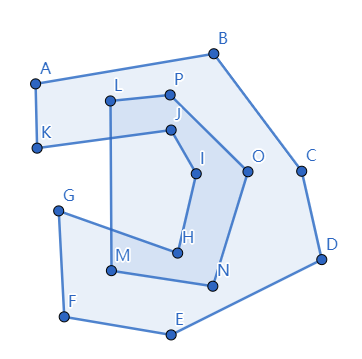
1. 点与平面

由一系列的点组成的多边形，与另外一个点的关系。如何判断点在平面内，还是平面外，平面的边上？计算出点与平面的最近距离，并计算最近距离的点的位置。

1.1 思路

  1. 先将多边形进行三角剖分，获得一个三角形 triangle 的集合 triangles ； - O(n⋅logn)O(n \cdot logn)

《06 - 多边形的三角剖分 - 单调划分》 - O(n⋅logn)O(n \cdot logn)
《06 - 多边形的三角剖分 - 耳切法》 - O(n2)O(n^2)

  1. 对 triangles 进行遍历，将其中每个三角形和点进行相交性检测 - O(n)O(n)

《01 - 数据结构定义》 4.3.2.2

1.2 示例代码

非完整

下列方法用返回的 int 值表示相交状态

  • res == -1 : 点在多边形内部
  • res == 0 : 点在多边形边上
  • res == 1 : 点在多边形外部
  1. 主算法
1
2
3
4
5
6
7
8
9
10
11
12
13
public int PointInPolygon(Point p, Polygon polygon){
    
    // 三角剖分
    ArrayList<Triangle> triangles = MonotonePartitioningAlgorithm.triangulate(polygon);

    for (Triangle t : triangles){
        if(t.PointInside(p) == -1) return -1;
        if(t.PointInside(p) == 0) return 0;
    }

    return 1;
}

  1. 判断点与三角形的相交关系（修改）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
public int PointInside(Point p) {

    // 检测点是否在三角形内部
    // 逆时针
    boolean l1 = Point.isLeftTurn(a, b, p);
    boolean l2 = Point.isLeftTurn(b, c, p);
    boolean l3 = Point.isLeftTurn(c, a, p);

    if (l1 && l2 && l3) {
            return -1;
    }
    
    // 顺时针
    boolean r1 = Point.isRightTurn(a, b, p);
    boolean r2 = Point.isRightTurn(b, c, p);
    boolean r3 = Point.isRightTurn(c, a, p);

    if (r1 && r2 && r3) {
        return -1;
    }

    // 检测点是否在三角形的三条边上
    boolean s1 = Segment.OnSegment(a, p, b);
    boolean s2 = Segment.OnSegment(b, p, c);
    boolean s3 = Segment.OnSegment(c, p, a);
    // 此处 OnSegment(p1, k, p2) 方法暂未实现
    /*
    OnSegment(p1, k, p2) 思路：
    1、 计算叉积 d = p1-k × p1-p2
    2、 若 k 在线段 p1-p2 上，须同时满足
        <1> d == 0
        <2> k的x坐标在 p1-p2 之间，x坐标相同时比较y坐标
    */

    if (s1 && s2 && s3) {
        return 0;
    }

    // 点在三角形外部
    return 1;
}

2. 直线与平面

由一系列的点组成的多边形，与另外一条直线的关系。如何判断直线切割平面，在平面外，与平面的边相交？计算出直线与平面的最近距离，并计算最近距离的点的位置。

1.1 思路

  1. 已知多边形端点的点集 vertices ，对点集中每个点进行遍历，点与直线的关系有三种：
    • 点在直线左边
    • 点在直线右边
    • 点在直线上

《01 - 数据结构定义》 3.2.13 public boolean isLeftPoint(Point p);
《01 - 数据结构定义》 3.2.14 public boolean isRightPoint(Point p);

  1. 之后根据对应的情况来进行判断：
    • 左边有点，右边有点：切割
    • 仅一边有点：
      • 存在部分点在直线上：相交
      • 不存在任何点在直线上：平面外

1.2 示例代码

非完整

下列方法用返回的 int 值表示相交状态

  • res == -1 : 直线切割平面
  • res == 0 : 直线相交平面
  • res == 1 : 直线在平面外部
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
public int LineInPolygon(Line l, Polygon polygon){
    ArrayList<Point> vertices = polygon.GetVertices();

    boolean pointInLeft = false;
    boolean pointInRight = false;
    boolean pointInLine = false;

    for(Point p : vertices){
        if(l.isLeftPoint(p)) pointInLeft = true;
        else if(l.isRightPoint(p)) pointInRight = true;
        else pointInLine = true;
    }

    // 直线左右均有多边形的端点：切割
    if(pointInLeft && pointInRight) return -1;

    // 直线仅一边有多边形的端点：
    // 存在部分点在直线上：相交
    if(pointInLine) return 0;
    // 不存在任何点在直线上：平面外
    else return 1;
}

3. 线段与平面

由一系列的点组成的多边形，与另外一条线段的关系。如何判断线段切割平面，在平面外，与平面的边相交？计算出线段与平面的最近距离，并计算最近距离的点的位置。

3.1 思路

  1. 对多边形的各个边维护一个集合 edges ，对边集合中的每个边与线段进行相交性检测

《02 - 两线段是否相交》

  1. 将多边形进行三角剖分，获得一个三角形 triangle 的集合 triangles ； - O(n⋅logn)O(n \cdot logn)

《06 - 多边形的三角剖分 - 单调划分》 - O(n⋅logn)O(n \cdot logn)
《06 - 多边形的三角剖分 - 耳切法》 - O(n2)O(n^2)

  1. 对 triangles 进行遍历，将其中每个三角形和端点进行相交性检测 - O(n)O(n)

《01 - 数据结构定义》 4.3.2.2

  1. 具体有以下情况：
    • 存在线段与边的相交：
      • 两端点均在多边形外部：线段与多边形完全切割
      • 两端点一外一内或者两端点均在内部：线段与多边形半切割
    • 不存在线段与边的相交：
      • 两端点均在外部：线段与多边形相离
      • 两端点均在内部：线段在多边形内部

4. 平面与平面

5、 由一系列的点组成的多边形，与另外一个平面的关系。如何判断平面与平面的关系，相交、分离、包含？计算出平面与平面的最近距离，并计算最近距离的点的位置。

4.1 思路 - O(n2)O(n^2)

  1. 将多边形 polygon_01 进行三角剖分，获得一个三角形 triangle 的集合 triangles_01 ； - O(n⋅logn)O(n \cdot logn)

《06 - 多边形的三角剖分 - 单调划分》 - O(n⋅logn)O(n \cdot logn)
《06 - 多边形的三角剖分 - 耳切法》 - O(n2)O(n^2)

  1. 对 triangles_01 进行遍历，将其中每个三角形和多边形 polygon_02顶点集 vertices_02 中的顶点两两进行相交性检测 - O(n)O(n)

《01 - 数据结构定义》 4.3.2.2

  1. 将 polygon_01 中的边 edges_01 与 polygon_02 中的边 edges_02 进行相交性检测

  2. 具体有以下情况：

  • 边有相交的情况：相交
  • 边没有相交的情况：
    • polygon_02 中的顶点均在 polygon_01 中：包含
    • polygon_02 中的顶点均在 polygon_01 外：分离

NOTE：必须进行边的相交性检测，因为顶点均在内的情况依旧有可能出现相交

screenShot.png