镜之国的爱丽丝
0%

01 - 数据结构定义

发表于 更新于 分类于

1. Point.class（点）

1.1 成员

$P_1 \to segment \gets P_2 $

1
2
3
4
5
6
7
final private double x;
final private double y;
    
private Segment segment;

// "not a point" 对象
public final static Point NaP = new Point(Double.NaN, Double.NaN);

1.2 方法

1.2.1 public void setSegment(Segment segment);

将线段附加到该点。

1
2
3
public void setSegment(Segment segment) {
    this.segment = segment;
}

1.2.2 private static double crossProduct(Point p0, Point p1, Point p2);

计算叉积

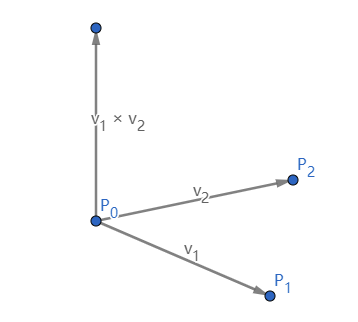
  • 两个由三个点 p0、p1 和 p2 定义的向量 (p0, p1) 和 (p0, p2)
1
2
3
4
private static double crossProduct(Point p0, Point p1, Point p2) {
    return (p1.getX() - p0.getX()) * (p2.getY() - p0.getY()) -
            (p2.getX() - p0.getX()) * (p1.getY() - p0.getY());
}

screenShot.png

定义：

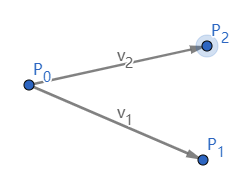
{v1⃗=(P0,P1)v2⃗=(P0,P2)\begin{cases} \vec{v_1} = (P_0,&P_1) \\ \vec{v_2} = (P_0,&P_2) \end{cases}

v1⃗×v2⃗=∣v1x⃗v2x⃗v1y⃗v2y⃗∣=∣(p1x−p0x)(p2x−p0x)(p1y−p0y)(p2y−p0y)∣\vec{v_1} \times \vec{v_2} = \begin{vmatrix} \vec{v_{1x}} & \vec{v_{2x}} \\ \vec{v_{1y}} & \vec{v_{2y}} \end{vmatrix} = \begin{vmatrix} (p_{1x} - p_{0x}) & (p_{2x} - p_{0x}) \\ (p_{1y} - p_{0y}) & (p_{2y} - p_{0y}) \end{vmatrix}

1.2.3 public double dist(Point p0);

计算该点到另一点的距离。

1
2
3
4
public double dist(Point p0) {
    return Math.sqrt((this.getX() - p0.getX()) * (this.getX() - p0.getX()) +
                    (this.getY() - p0.getY()) * (this.getY() - p0.getY()));
    }

1.2.4 public static boolean isLeftTurn(Point p0, Point p1, Point p2);

确认向量<p0, p1> 到 <p0, p2>是否为左转（右手坐标系下，逆时针旋转）

1
2
3
public static boolean isLeftTurn(Point p0, Point p1, Point p2) {
    return (crossProduct(p0, p1, p2) > 0);
}

screenShot.png

1.2.5 public static boolean isRightTurn(Point p0, Point p1, Point p2);

确认向量<p0, p1> 到 <p0, p2>是否为右转（右手坐标系下，顺时针旋转）

1
2
3
public static boolean isRightTurn(Point p0, Point p1, Point p2) {
    return (crossProduct(p0, p1, p2) < 0);
}

screenShot.png

1.2.6 public boolean isLeft();

确定该点是否为附加线段的左顶点。

1
2
3
public boolean isLeft() {
    return (segment != null && this.equals(segment.getLeft()));
}

1.2.7 public boolean isRight();

确定该点是否为附加线段的右顶点。

1
2
3
public boolean isRight() {
    return (segment != null && this.equals(segment.getRight()));
}

1.2.8 public boolean isNaP();

确定该点是否等于 Point.NaP

1
2
3
public boolean isNaP() {
    return x == Double.NaN || y == Double.NaN;
}

2. Segment.class（线段）

2.1 成员

一个线段的左右端点

1
2
final private Point left;
final private Point right;

2.2 方法

2.2.1 构造方法 public Segment(Point left, Point right);

1
2
3
4
5
6
7
8
9
10
11
12
13
14
public Segment(Point left, Point right) {

    if(left.getX() > right.getX()) {
        Point temp = right;
        right = left;
        left = temp;
    }
    
    left.setSegment(this);
    right.setSegment(this);
    
    this.left = left;
    this.right = right;
}

2.2.2 public Point getBisectionalPoint();

返回线段的二等分中点坐标。

1
2
3
4
public Point getBisectionalPoint() {
    return new Point((left.getX() + right.getX()) / 2,
                    (left.getY() + right.getY()) / 2);
}

2.2.3 public Line getLine();

返回线段所在的直线。

1
2
3
public Line getLine() {
        return new Line(left, right);
    }

3. Line.class（直线）

3.1 成员

用三个系数表示一条线
a、b 和 c，其中 ax + by + c = 0。

1
private double a, b, c;

3.2 方法

3.2.1 构造方法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
// 用三个系数初始化一条线
public Line(double a, double b, double c) {
    this.a = a;
    this.b = b;
    this.c = c;
}

// 用两个不同的点坐标初始化一条线
public Line(Point p1, Point p2) {
    this.a = p1.getY() - p2.getY();
    this.b = p2.getX() - p1.getX();
    this.c = p1.getX() * p2.getY() - p2.getX() * p1.getY();
}

// 用线段初始化
public Line(Segment s) {
    this(s.getLeft(), s.getRight());
}

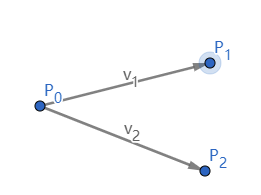
定义：

{a=p1y−p2yb=p2x−p1xc=p1x⋅p2y−p2x⋅p1y\begin{cases} a = p_{1y} - p_{2y} \\ b = p_{2x} - p_{1x} \\ c = p_{1x} \cdot p_{2y} - p_{2x} \cdot p_{1y} \end{cases}

3.2.3 public double XforY(double y);

通过直线上某点的 Y 坐标计算它的 X 坐标

1
2
3
public double XforY(double y) {
    return (-c - b*y) / a;
}

定义：

x=−c−b⋅yax = \frac {-c - b \cdot y} {a}

3.2.4 public double YforX(double x);

通过直线上某点的 X 坐标计算它的 Y 坐标

1
2
3
public double YforX(double x) {
    return (-c - a*x) / b;
}

定义：

y=−c−a⋅xby = \frac {-c - a \cdot x} {b}

3.2.5 public boolean pointOnLine(Point p);

判断某点是否位于直线上。

1
2
3
public boolean pointOnLine(Point p) {
    return (a*p.getX() + b*p.getY() + c == 0);
}

3.2.6 public boolean isAscending();

确定直线是否递增
与 X 轴的方向成一个角度（0，pi/2）

1
2
3
public boolean isAscending() {
    return (b == 0 || (-a/b) >= 0);
}

3.2.7 public boolean isVertical();

确定直线是否垂直
与 X 轴的方向成一个角度 pi/2

1
2
3
public boolean isVertical() {
    return (b == 0 && a != 0);
}

3.2.8 public boolean isDescending();

确定直线是否递减
与 X 轴的方向成一个角度（pi/2，pi）

1
2
3
public boolean isDescending() {
    return (b == 0 || (-a/b) < 0);
}

3.2.9 public boolean isHorizontal();

确定直线是否水平
与 X 轴的方向成一个角度 pi

1
2
3
public boolean isHorizontal() {
    return (a == 0 && b != 0);
}

3.2.10 public boolean isUndefined();

判断直线是否为“未定义”（Undefined）
（例如，将两个相等的点传递给构造函数）

1
2
3
public boolean isUndefined() {
    return (a == 0 && b == 0 && c == 0);
}

3.2.11 public double getAngle();

以 X 轴的正方向，计算直线形成的角度

1
2
3
4
5
6
7
8
9
public double getAngle() {
    if (isVertical()) 
        return Math.PI/2;
    
    double arctan = Math.atan(-a/b);
    if (arctan < 0) arctan += Math.PI;
    
    return arctan;
}

3.2.12 public Line getPerpendicularLine(Point p);

通过给定点计算垂直线。

1
2
3
public Line getPerpendicularLine(Point p) {
    return new Line(this.b, -this.a, -this.b*p.getX() + this.a*p.getY());
}

定义：

{A=bB=−aC=−b⋅px+a⋅py\begin{cases} A = b \\ B = - a \\ C = - b \cdot p_x + a \cdot p_y \end{cases}

垂线：

b⋅x−a⋅y−b⋅px+a⋅py=0b \cdot x - a \cdot y - b \cdot p_x + a \cdot p_y = 0

3.2.13 public boolean isLeftPoint(Point p);

确定点是否位于直线的左半部分

1
2
3
public boolean isLeftPoint(Point p) {
    return p.getX() < XforY(p.getY());
}

3.2.14 public boolean isRightPoint(Point p);

确定点是否位于直线的右半部分

1
2
3
public boolean isRightPoint(Point p) {
    return p.getX() > XforY(p.getY());
}

3.2.15 public static Point intersection(Line l1, Line l2);

计算两条直线的交点。

1
2
3
4
5
6
7
8
9
public static Point intersection(Line l1, Line l2) {
    if((l1.a*l2.b - l2.a*l1.b) == 0)
        return Point.NaP;

    double x = (l1.b*l2.c - l2.b*l1.c) / (l1.a*l2.b - l2.a*l1.b);
    double y = (l2.a*l1.c - l1.a*l2.c) / (l1.a*l2.b - l2.a*l1.b);

    return new Point(x, y);
}

定义：

{L1:a1x+b1y+c1=0L2:a2x+b2y+c2=0⇒{x=b1c2−b2c1a1b2−a2b1y=a2c1−a1c2a1b2−a2b1\begin{cases} L_1 : a_1x + b_1y + c_1 = 0 \\[3ex] L_2 : a_2x + b_2y + c_2 = 0 \end{cases} \Rightarrow \begin{cases} x = \frac {b_1c_2 - b_2c_1} {a_1b_2 - a_2b_1} \\[3ex] y = \frac {a_2c_1 - a_1c_2} {a_1b_2 - a_2b_1} \end{cases}

  • 唯一解：分母 (a1b2−a2b1)(a_1b_2 - a_2b_1) 为非零值。
  • 无解：分母为零，两条直线平行。
  • 无穷多解：分母为零，两条直线重合。

4. Triangle.class（三角形）

4.1 成员

1
2
3
4
5
6
7
8
9
10
11
/** 顶点 **/
protected Point a, b, c;

/** 指向相邻的三个三角形的指针 **/
protected Triangle adjAB, adjBC, adjAC;

/**
* 标记以存储一些附加信息
* （例如，将三角形与某些数据结构连接起来）。
*/
private Object tag;
  • 三角形三条边的枚举
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/*
* 三角形边的枚举。
*/
public enum Side {
    AB(0), BC(1), AC(2);
    
    Side(int i) {
        this.i = i;
    }
    
    /**
        * 返回其索引的三角形边，
        * 其中 AB 是第 0 边，
        * 第一个是 BC，第二个是 AC。
        * 
        * @param i The index
        * @return 如果索引不正确，则返回 side 或 null
        */
    public static Side valueOf(int i) {
        switch(i) {
            case 0: return AB;
            case 1: return BC;
            case 2: return AC;
            default: return null;
        }
    }
    
    int i;
}

4.2 接口

4.2.1 原型

1
public class Triangle implements Cloneable;

仅做浅复制，初始化三个指针

1
2
3
4
5
6
7
8
9
10
11
@Override
public Object clone() {
    
    Triangle res = (Triangle)super.clone();
    // res.adjAB = this.adjAB;
    // res.adjBC = this.adjBC;
    // res.adjAC = this.adjAC;
    // res.tag = this.tag;
    
    return res;
}

4.3 方法

通过其顶点初始化三角形。
注意：更改顶点的顺序
使其逆时针旋转。

4.3.1 构造方法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public Triangle (Point A, Point B, Point C) {
    a = A;
    b = B;
    c = C;
    adjAB = adjAC = adjBC = null;

    // 构造逆时针表示的三角形
    // 该步骤在进行三角剖分时必不可少
    double sum = (b.getX() - a.getX())*
                    (b.getY() + a.getY()) + 
                    (c.getX() - b.getX())*
                    (c.getY() + b.getY()) +
                    (a.getX() - c.getX())*
                    (a.getY() + c.getY());
    
    // 顺时针三角形用该公式求得的面积为正
    // 若面积为正，则为顺时针，需要改为逆时针表示法
    if (sum > 0) {
        Point temp = a;
        a = b;
        b = temp;
    }
}

△ABC\triangle ABC 的有符号面积（该处以顺时针表示的三角形为例）：

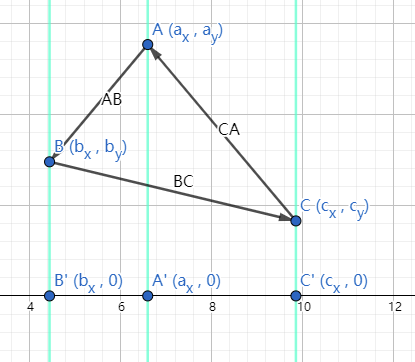
  • 有符号面积：若边的端点从左至右，则面积为正；若边的端点从右至左，则面积为负

screenShot.png

NOTE：其中 S梯CC′A′AS_{梯CC'A'A} 的面积应该为负，即

S梯CC′A′A=−12(cx−ax)(cy+ay)=12(ax−cx)(cy+ay)\begin{aligned} S_{梯CC'A'A} &= - \frac {1} {2} (c_x - a_x)(c_y + a_y) \\ &= \frac {1} {2} (a_x - c_x)(c_y + a_y) \end{aligned}

可得：

{S梯AA′B′B=12(bx−ax)(by+ay)S梯BB′C′C=12(cx−bx)(cy+by)S梯CC′A′A=12(ax−cx)(cy+ay)\begin{cases} S_{梯AA'B'B} = \frac {1} {2} (b_x - a_x)(b_y + a_y) \\ S_{梯BB'C'C} = \frac {1} {2} (c_x - b_x)(c_y + b_y) \\ S_{梯CC'A'A} = \frac {1} {2} (a_x - c_x)(c_y + a_y) \end{cases}

即：

S△ABC=S梯AA′B′B+S梯BB′C′C+S梯CC′A′A=12[(bx−ax)⋅(by+ay)+(cx−bx)⋅(cy+by)+(ax−cx)⋅(ay+cy)]\begin{aligned} S_{\triangle ABC} &= S_{梯AA'B'B} + S_{梯BB'C'C} + S_{梯CC'A'A} \\ &= \frac {1} {2}[(b_x - a_x) \cdot (b_y + a_y) + (c_x - b_x) \cdot (c_y + b_y) + (a_x - c_x) \cdot (a_y + c_y)] \end{aligned}

显然：

  • S△ABC>0S_{\triangle ABC} \gt 0：三角形顺时针表示
  • S△ABC<0S_{\triangle ABC} \lt 0：三角形逆时针表示（如下图所示）

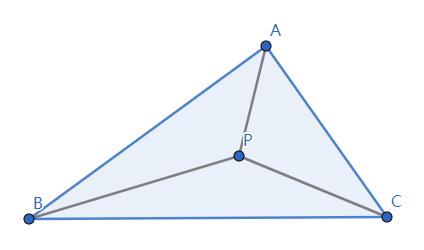
screenShot.png

4.3.2 public boolean pointInside(Point p);

确定点是否位于三角形内。

  1. public boolean pointInside(Point p);
1
2
3
public boolean pointInside(Point p) {
    return pointInside(p, true);
}
  1. public boolean pointInside(Point p, boolean strict);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
public boolean pointInside(Point p, boolean strict) {
    
    // (strict == true) : 点在边界时不算在三角形上
    if (strict) {
        
        // 逆时针
        boolean l1 = Point.isLeftTurn(a, b, p);
        boolean l2 = Point.isLeftTurn(b, c, p);
        boolean l3 = Point.isLeftTurn(c, a, p);

        if (l1 && l2 && l3) {
            return true;
        }

        // 顺时针
        boolean r1 = Point.isRightTurn(a, b, p);
        boolean r2 = Point.isRightTurn(b, c, p);
        boolean r3 = Point.isRightTurn(c, a, p);

        if (r1 && r2 && r3) {
            return true;
        }

        return false;
    
    // (strict == false) : 点在边界时算在三角形上
    } else {
        
        boolean l1 = ! Point.isRightTurn(a, b, p);
        boolean l2 = ! Point.isRightTurn(b, c, p);
        boolean l3 = ! Point.isRightTurn(c, a, p);
        // isLeftTurn（点在三角形内） || 点在边界上

        if (l1 && l2 && l3) {
            return true;
        }

        boolean r1 = ! Point.isLeftTurn(a, b, p);
        boolean r2 = ! Point.isLeftTurn(b, c, p);
        boolean r3 = ! Point.isLeftTurn(c, a, p);

        if (r1 && r2 && r3) {
            return true;
        }

        return false;
    }
}

  • 逆时针三角形
    isLeftTurn(a, b, p)：A -> B -> P 逆时针
    screenShot.png

  • 顺时针三角形
    isRightTurn(a, b, p)：A -> B -> P 顺时针
    screenShot.png

4.3.3 public boolean pointOnTheEdge(Point p);

确定点是否位于三角形的边上。

1
2
3
4
5
public boolean pointOnTheEdge(Point p) {
    return getSideLine(Side.AB).pointOnLine(p) ||
            getSideLine(Side.BC).pointOnLine(p) ||
            getSideLine(Side.AC).pointOnLine(p);
}

4.3.4 public boolean pointInTheInterior(Point p);

确定点是否位于三角形的内部。

1
2
3
public boolean pointInTheInterior(Point p) {
    return ! pointOnTheEdge(p);
}

4.3.5 public Side getPointSide(Point p);

返回点 P 所在三角形的边

1
2
3
4
5
6
7
8
9
10
11
public Side getPointSide(Point p) {
    if (getSideLine(Side.AB).pointOnLine(p)) {
        return Side.AB;
    } else if (getSideLine(Side.BC).pointOnLine(p)) {
        return Side.BC;
    } else if (getSideLine(Side.AC).pointOnLine(p)) {
        return Side.AC;
    } else {
        return null;
    }
}

4.3.6 public Line getSideLine(Side s);

返回三角形的边所在的直线

1
2
3
4
5
6
7
8
public Line getSideLine(Side s) {
    switch(s) {
        case AB: return new Line(this.getA(), this.getB());
        case BC: return new Line(this.getB(), this.getC());
        case AC: return new Line(this.getA(), this.getC());
        default: return null;
    }
}

4.3.7 public Segment getSide(Side s);

返回三角形的边。

1
2
3
4
5
6
7
8
public Segment getSide(Side s) {
    switch(s) {
        case AB: return new Segment(this.getA(), this.getB());
        case BC: return new Segment(this.getB(), this.getC());
        case AC: return new Segment(this.getA(), this.getC());
        default: return null;
    }
}

4.3.8 getPoint 方法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
public Point getA() {
    return a;
}

public Point getB() {
    return b;
}

public Point getC() {
    return c;
}

public Point getIth(int i) {
    switch (i) {
        case 0: return a; 
        case 1: return b;
        case 2: return c;
        default: return null;
    }
}

private void setIth(int i, Point p) {
    switch (i) {
        case 0: a = p; break;
        case 1: b = p; break;
        case 2: c = p; break;
    }
}

4.3.9 Adjacent 方法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
// 设置三角形的边
private void setAdjacent(Side thisSide, Triangle t) {
    switch (thisSide) {
        case AB: this.adjAB = t; break;
        case BC: this.adjBC = t; break;
        case AC: this.adjAC = t; break;
    }
}

// 获得三角形的边
public Triangle getAdjacent(Side s) {
    switch (s) {
        case AB: return adjAB;
        case BC: return adjBC;
        case AC: return adjAC;
        default: return null;
    }
}

// 查看是否 this 的 s 边指向对应的 t 
public boolean isAdjacent(Triangle t, Side s) {
    return this.getAdjacent(s) == t;
}

4.3.10 public Side getAdjacentSide(Side s);

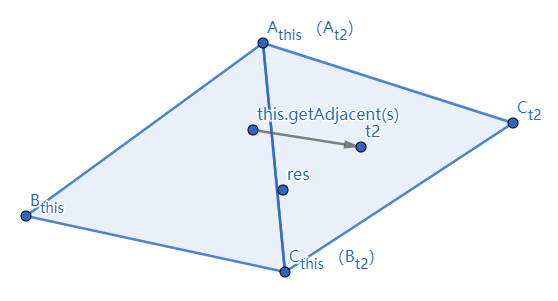
返回与当前三角形某条边相邻的另一侧的边。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
public Side getAdjacentSide(Side s) {
    Triangle t2 = this.getAdjacent(s);

    Triangle.Side res = null;
    if (t2 != null) {
        for (Triangle.Side sd : Triangle.Side.values()) {
            if (t2.isAdjacent(this, sd)) {
                res = sd;
                break;
            }
        }
    }
    return res;
}

screenShot.png

  • 该处的this.getAdjacent(s)即为this.adjAC，指向三角形t2
  • 返回的 res 在该处即为 Side.AB

4.3.11 public boolean link(Triangle t);

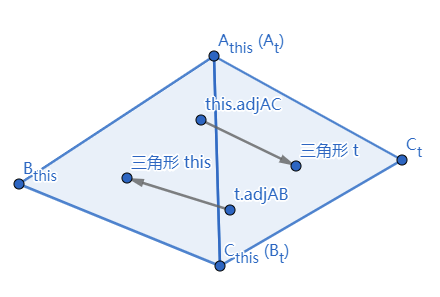
更新给定另一个三角形的相邻三角形的链接
两个三角形中的链接都将更新

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
public boolean link(Triangle t) {
    
    if (t == null) {
        return false;
    }
    
    Segment s1, s2;
    for (int i = 0; i <= 2; i++) {
        for (int j = 0; j <= 2; j++) {
            s1 = new Segment(this.getIth(i), this.getIth((i+1) % 3));
            s2 = new Segment(t.getIth(j), t.getIth((j+1) % 3));
            
            if (s1.equals(s2)) {
                
                Side sThis = Side.valueOf(i);
                Side sT = Side.valueOf(j);
                
                this.setAdjacent(sThis, t);
                t.setAdjacent(sT, this);
                
                return true;
            }
        }
    }
    
    return false;
}

{s1=[A1B1,B1C1,C1A1]s2=[A2B2,B2C2,C2A2]\begin{cases} s_1 = [A_1B_1, B_1C_1, C_1A_1] \\ s_2 = [A_2B_2, B_2C_2, C_2A_2] \end{cases}

两两组合进行匹配，若为“同一个边”，则在该两个三角形之间，维护一个双向链表指针
图例中 i == 2 && j == 0
screenShot.png

4.3.12 Tag 方法

1
2
3
4
5
6
7
public Object getTag() {
    return tag;
}

public void setTag(Object t) {
    this.tag = t;
}

4.3.13 public boolean containsVertex(Point p);

确定该点是否为当前三角形的顶点。

1
2
3
public boolean containsVertex(Point p) {
    return a.equals(p) || b.equals(p) || c.equals(p);
}

4.3.14 public void flipEdge(Side s1, Triangle t2, Side s2);（存疑）

翻转两个三角形的公共边（原地翻转）。
假设相邻的边都正确的给出。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
public void flipEdge(Side s1, Triangle t2, Side s2) {
        
    if (! (this.getAdjacent(s1).equals(t2) &&
        t2.getAdjacent(s2).equals(this))) {
        
        return;
    }
    
    // 获取下标
    int i = s1.ordinal();
    int j = s2.ordinal();
    
    Triangle adjTemp1 = this.getAdjacent(Side.valueOf((i+1) % 3));
    Triangle adjTemp2 = t2.getAdjacent(Side.valueOf((j+1) % 3));
    
    Point c1 = this.getIth((i+1) % 3);

    Point a2 = this.getIth(i);
    Point b2 = this.getIth((i+2) % 3);
    Point c2 = t2.getIth((j+2) % 3);
    
    // Update points (this)
    
    this.setIth(i, a2);
    this.setIth((i+1) % 3, c2);
    this.setIth((i+2) % 3, b2);
    
    //Update adjacent triangles (!) 
    
    this.setAdjacent(Side.valueOf(i), adjTemp2);
    this.setAdjacent(Side.valueOf((i+1) % 3), t2);
    //this.setAdjacent(Side.valueOf((i+2) % 3), this.getAdjacent(Side.valueOf((i+2) % 3)));

    // Update points (t2)
    
    t2.setIth(j, c1);
    t2.setIth((j+1) % 3, b2);
    t2.setIth((j+2) % 3, c2);
    
    //Update adjacent triangles (!) 
    
    t2.setAdjacent(Side.valueOf(j), adjTemp1);
    t2.setAdjacent(Side.valueOf((j+1) % 3), this);
    //t2.setAdjacent(Side.valueOf((j+2) % 3), t2.getAdjacent(Side.valueOf((j+2) % 3)));
    
    // Some other changes
    
    if (adjTemp1 != null) {
        adjTemp1.link(t2);
    }
    if (adjTemp2 != null) {
        adjTemp2.link(this);
    }
}
  • s[i] 和 P[i] 的对应关系

i=0⇒AB→:Ai=1⇒BC→:Bi=2⇒CA→:C\begin{aligned} i = 0 \Rightarrow \overrightarrow{AB} : A \\ i = 1 \Rightarrow \overrightarrow{BC} : B \\ i = 2 \Rightarrow \overrightarrow{CA} : C \end{aligned}

5. Circle.class

5.1 成员

1
2
private Point center;
private double radius;

5.2 方法

5.2.1 构造方法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public Circle(Point center, double radius) {
    this.center = center;
    this.radius = radius;
}

// 通过圆边界上的三个不同点初始化圆。
public Circle(Point a, Point b, Point c) {
    Line l1 = new Line(2*a.getX() - 2*b.getX(),
                        2*a.getY() - 2*b.getY(),
                        b.getX()*b.getX() - a.getX()*a.getX() +
                        b.getY()*b.getY() - a.getY()*a.getY());
    Line l2 = new Line(2*a.getX() - 2*c.getX(),
                        2*a.getY() - 2*c.getY(),
                        c.getX()*c.getX() - a.getX()*a.getX() +
                        c.getY()*c.getY() - a.getY()*a.getY());
    
    center = Line.intersection(l1, l2); 
    // 可能为 NaP (如果a，b，c是共线的).
    radius = center.dist(a);
}

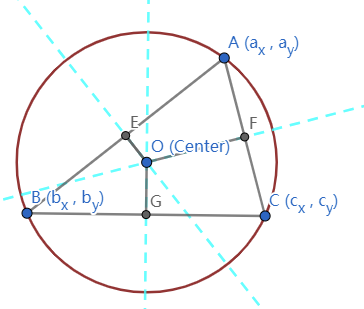
screenShot.png

  • 代码中的直线 l1 为图中的直线 OEOE
  • 代码中的直线 l2 为图中的直线 OFOF
  • 圆心坐标即为两条直线的交点
  • 半径 r=∣OA∣r = | OA |

以直线 OEOE 为例：

  • 斜率：（AB⊥OEAB \bot OE）

kAB=ay−byax−bx⇒kOE=−ax−bxay−by\begin{aligned} k_{AB} &= \frac {a_y - b_y} {a_x - b_x} \\[3ex] \Rightarrow k_{OE} &= - \frac {a_x - b_x} {a_y - b_y} \end{aligned}

  • 该直线过线段 ABAB 的中点 E(ax+bx2,ay+by2)E (\frac {a_x + b_x} {2}, \frac {a_y + b_y} {2})

OE:y=−ax−bxay−byx+m⇒OE:(ax−bx)x+(ay−by)y+C=0⇒OE:(ax−bx)(ax+bx2)+(ay−by)(ay+by2)+C=0⇒C=12(bx2−ax2+by2−ay2)\begin{aligned} &OE : y = - \frac {a_x - b_x} {a_y - b_y} x + m \\[3ex] \Rightarrow &OE : (a_x - b_x)x + (a_y - b_y)y + C = 0 \\[3ex] \Rightarrow &OE : (a_x - b_x)(\frac {a_x + b_x} {2}) + (a_y - b_y)(\frac {a_y + b_y} {2}) + C = 0 \\[3ex] \Rightarrow &C = \frac {1} {2}(b_x^2 - a_x^2 + b_y^2 - a_y^2) \end{aligned}

  • 可得直线 OEOE 的系数分别为：

{A=2(ax−bx)B=2(ay−by)C=bx2−ax2+by2−ay2\begin{cases} A = 2(a_x - b_x) \\[2ex] B = 2(a_y - b_y) \\[2ex] C = b_x^2 - a_x^2 + b_y^2 - a_y^2 \end{cases}

  • 同理可得，直线 OFOF 的系数分别为：

{A=2(ax−cx)B=2(ay−cy)C=cx2−ax2+cy2−ay2\begin{cases} A = 2(a_x - c_x) \\[2ex] B = 2(a_y - c_y) \\[2ex] C = c_x^2 - a_x^2 + c_y^2 - a_y^2 \end{cases}

5.2.2 get 方法

1
2
3
4
5
6
7
public Point getCenter() {
    return center;
}

public double getRadius() {
    return radius;
}

5.2.3 圆与点的位置关系

1
2
3
4
5
6
7
8
9
// 确定给定点是否位于圆内
public boolean isInside(Point p) {
    return center.dist(p) < radius;
}

// 确定给定点是否位于圆的外部
public boolean isOutside(Point p) {
    return center.dist(p) > radius;
}

6. Polygon.class

6.1 成员

1
2
3
4
5
// 点集
private ArrayList<Point> vertices;

// 是否顺时针
private boolean isClockwise;

6.2 接口

6.2.1 原型

1
public class Polygon implements Cloneable;

深复制，拷贝点集中所有的点

1
2
3
4
5
6
7
8
9
@Override
public Object clone() {
    
    Polygon copy = new Polygon();
    
    copy.vertices = (ArrayList<Point>)this.vertices.clone();
    
    return copy;
}

6.3 方法

6.3.1 构造方法

1
2
3
4
5
6
7
8
9
// 初始化一个空的多边形
public Polygon() {
    vertices = new ArrayList<Point>();
}

// 通过一个点集初始化一个多边形
public Polygon(ArrayList<Point> vertices) {
    this.vertices = (ArrayList<Point>)vertices.clone();
}

6.3.2 点集的操作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
// 添加点到点集
public void add(Point p) {
    if (p != null) {
        vertices.add(p);
    }
}

// 通过索引从点集移除对应的点
public void remove(int i) {
    if (i >= 0 && i < size()) {
        vertices.remove(i);
    }
}

// 通过索引从点集获得对应的点
public Point get(int i) {
    if (i >= 0 && i < size()) {
        return vertices.get(i);
    } else {
        return null;
    }
}

public int size() {
    return vertices.size();
}

public boolean isEmpty() {
    return vertices.isEmpty();
}

6.3.3 public Polygon subPolygon(int start, int end);

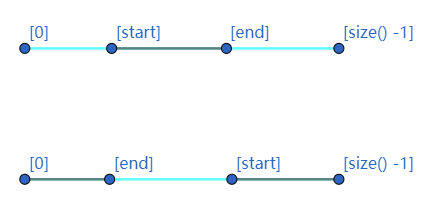
创建当前多边形的子多边形

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public Polygon subPolygon(int start, int end) {
    Polygon p = new Polygon();

    if (start < end) {
        for(int i = start; i <= end; i++) {
            p.add(get(i));
        }

    } else if (start > end) {
        for(int i = start; i < size(); i++) {
            p.add(get(i));
        }
        for(int i = 0; i <= end; i++) {
            p.add(get(i));
        }
    }
    
    p.isClockwise = this.isClockwise;
    return p;
}

screenShot.png

6.3.4 确定多边形的凹凸性

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
// 确定顶点是否为凸面（并使多边形成为 “ear”）
public boolean isConvex(int i) {
    int prev = (i - 1 + size()) % size();
    int next = (i + 1) % size();
    
    // 异或运算符
    return (Point.isLeftTurn(get(prev), get(i), get(next))
            ^ isClockwise);
}

// 确定多边形是否为凸面。
public boolean isConvex() {
    
    for (int i = 0; i < size(); i++) {
        if (! isConvex(i)) {
            return false;
        }
    }
    
    return true;
}

以逆时针为例（ i=2i = 2 ）：

screenShot.png

显然：

  • Point.isLeftTurn(1, 2, 3) == true : isClockwise == false（逆时针）
  • Point.isLeftTurn(1, 2, 3) == false : isClockwise == true（顺时针）

6.3.5 public boolean isClockwise();

确定列表中顶点的顺序是否为顺时针

1
2
3
4
5
6
7
8
9
10
11
public boolean isClockwise() {
    double sum = 0;
    
    for (int i = 0; i < size(); i++) {
        sum += (vertices.get((i+1)%size()).getX() - vertices.get(i).getX())*
                (vertices.get((i+1)%size()).getY() + vertices.get(i).getY());
    }
    
    isClockwise = (sum > 0);
    return isClockwise;
}

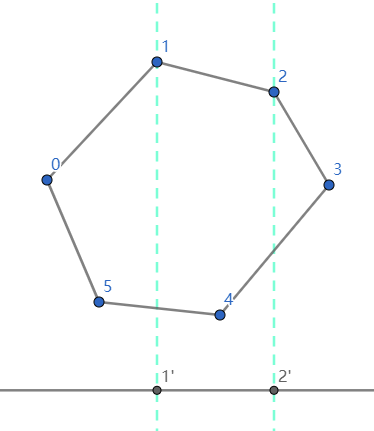
以顺时针多边形为例 ( i=1i = 1 )：

screenShot.png

S梯11′2′2=12(2x−1x)(2y+2x)S_{梯11'2'2} = \frac{1}{2} (2_x - 1_x)(2_y + 2_x)

  • S多边形>0S_{多边形} > 0 : 顺时针
  • S多边形<0S_{多边形} < 0 : 逆时针

7. Halfplane.class

  • 半平面用一条边界线表示 ax + by = c
  • 对于半平面，ax + by + c <= 0 成立。

7.1 成员

1
2
3
4
5
// 边界线
private Line line;

// 平面的朝向
private boolean rightSide;

7.2 方法

7.2.1 构造方法

1
2
3
4
public Halfplane(Line line, boolean rightSide) {
    this.line = line;
    this.rightSide = rightSide;
}

7.2.2 get 方法

1
2
3
public Line getLine() {
    return line;
}

7.2.3 判断平面的朝向

1
2
3
4
5
6
7
8
9
// 确定边界线是否位于半平面的左侧。
public boolean isLeftBoundary() {
    return rightSide;
}

// 确定边界线是否位于半平面的右侧。
public boolean isRightBoundary() {
    return ! rightSide;
}

7.2.4 public boolean includes(Point p);

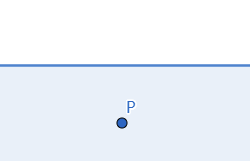
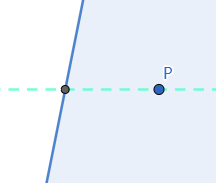
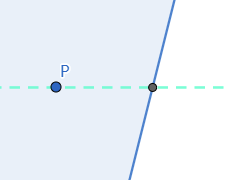
确定该点是否位于半平面中

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public boolean includes(Point p) {
    
    if (isLeftBoundary()) {
        
        // 分界线水平时，为平面的上限，半平面朝下
        if (line.isHorizontal()) {
            return (p.getY() < line.YforX(0));
        } else {
            return (p.getX() > line.XforY(p.getY()));
        }
        
    } else {

        // 分界线水平时，为平面的下限，半平面朝上
        if (line.isHorizontal()) {
            return (p.getY() > line.YforX(0));
        } else {
            return (p.getX() < line.XforY(p.getY()));
        }
    }
}

  • isLeftBoundary() == true（边界线位于半平面的左侧，平面朝右）

    • line.isHorizontal() == true（分界线水平时，为平面的上限，半平面朝下）
      screenShot.png

    • line.isHorizontal() == false（非水平线）
      screenShot.png

  • isLeftBoundary() == false（边界线位于半平面的右侧，平面朝左）

    • line.isHorizontal() == true（分界线水平时，为平面的下限，半平面朝上）
      screenShot.png

    • line.isHorizontal() == false（非水平线）
      screenShot.png

7.2.5 public static ArrayList boundingRectangle(double x1, double x2, double y1, double y2)

用边界矩形初始化一组半平面

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
public static ArrayList<Halfplane> boundingRectangle(double x1, double x2,
                                                    double y1, double y2) {

    ArrayList<Halfplane> res = new ArrayList<Halfplane>();

    // 将传入的坐标重新设置为左斜上方向
    // 令其满足 (x1 < x2) && (y1 < y2)
    if (x1 > x2) {
        double temp = x1;
        x1 = x2;
        x2 = temp;
    }

    if (y1 > y2) {
        double temp = y1;
        y1 = y2;
        y2 = temp;
    }

    res.add(new Halfplane(new Line(new Point(x1, 0), new Point(x1, 1)), true));
    res.add(new Halfplane(new Line(new Point(0, y2), new Point(1, y2)), true));
    res.add(new Halfplane(new Line(new Point(x2, 0), new Point(x2, 1)), false));
    res.add(new Halfplane(new Line(new Point(0, y1), new Point(1, y1)), false));

    return res;
}

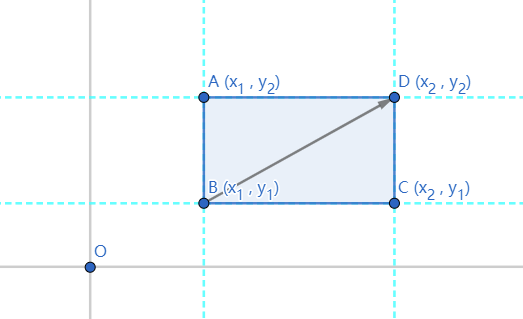
screenShot.png

图中：

  • Line(new Point(x1, 0), new Point(x1, 1)) : 直线 ABAB
  • Line(new Point(0, y2), new Point(1, y2)) : 直线 ADAD
  • Line(new Point(x2, 0), new Point(x2, 1)) : 直线 CDCD
  • Line(new Point(0, y1), new Point(1, y1)) : 直线 BCBC

参考源代码：