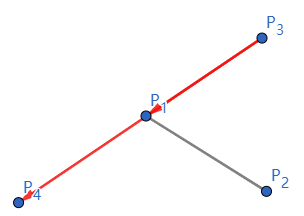
1. 算法思路:
略
时间复杂度:O(1)
2. 实例代码:
2.1 import
1
2
| import primitives.Point;
import primitives.Segment;
|
2.2 SegmentsIntersect.class
2.2.1 方法
2.2.1.1 叉乘确定两线段的相对位置
1
2
3
4
| private static double direction(Point p0, Point p1, Point p2) {
return ((p2.getX() - p0.getX()) * (p1.getY() - p0.getY()) -
(p2.getY() - p0.getY()) * (p1.getX() - p0.getX()));
}
|
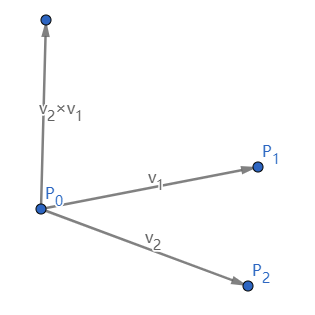
定义:
{v1=(P0,v2=(P0,P1)P2)
v2×v1=∣∣∣∣v2xv2yv1xv1y∣∣∣∣=∣∣∣∣(p2x−p0x)(p2y−p0y)(p1x−p0x)(p1y−p0y)∣∣∣∣
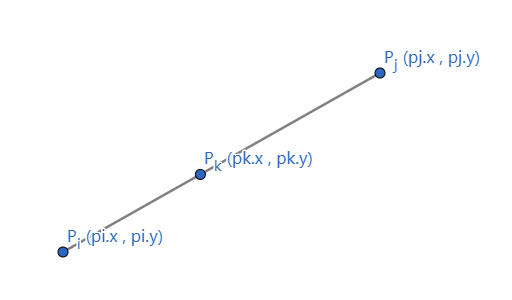
2.2.1.2 确定三点的相对位置
1
2
3
4
5
6
| private static boolean onSegment(Point pi, Point pj, Point pk) {
return (Math.min(pi.getX(), pj.getX()) <= pk.getX() &&
pk.getX() <= Math.max(pi.getX(), pj.getX()) &&
Math.min(pi.getY(), pj.getY()) <= pk.getY() &&
pk.getY() <= Math.max(pi.getY(), pj.getY()));
}
|
2.2.1.3 检测两线段是否相交
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| public static boolean two(Segment s1, Segment s2) {
Point p1 = s1.getLeft();
Point p2 = s1.getRight();
Point p3 = s2.getLeft();
Point p4 = s2.getRight();
double d1 = direction(p3, p4, p1);
double d2 = direction(p3, p4, p2);
double d3 = direction(p1, p2, p3);
double d4 = direction(p1, p2, p4);
if (((d1 > 0 && d2 < 0) || (d1 < 0 && d2 > 0)) &&
((d3 > 0 && d4 < 0) || (d3 < 0 && d4 > 0))) {
return true;
} else if (d1 == 0 && onSegment(p3, p4, p1)) {
return true;
} else if (d2 == 0 && onSegment(p3, p4, p2)) {
return true;
} else if (d3 == 0 && onSegment(p1, p2, p3)) {
return true;
} else if (d4 == 0 && onSegment(p1, p2, p4)) {
return true;
} else {
return false;
}
}
|
-
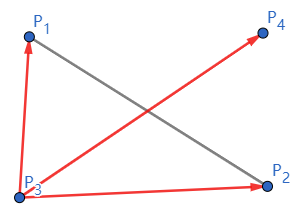
(d1 > 0 && d2 < 0) || (d1 < 0 && d2 > 0) : P3P4 在 P3P1 和 P3P2 之间
{P3P1×P3P4>0P3P2×P3P4<0
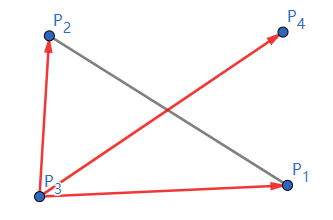
{P3P1×P3P4<0P3P2×P3P4>0
-
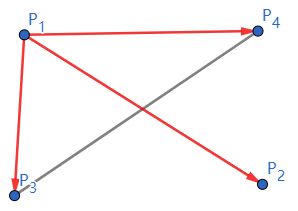
(d3 > 0 && d4 < 0) || (d3 < 0 && d4 > 0) : P1P2 在 P1P3 和 P1P4 之间
{P1P3×P1P2>0P1P4×P1P2<0
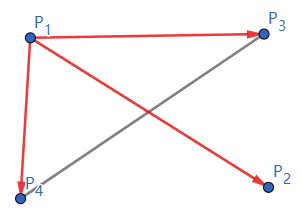
{P1P3×P1P2<0P1P4×P1P2>0
_
d1 == 0 : P3 , P4 , P1 三点共线:P3P1×P3P4=0onSegment(p3, p4, p1) == true : 点 P1 在点 P3 , P4 之间