1. 算法思路

1. 对端点集合 $points$ 进行排序，形成有序端点序列 $points$

2. 维护一个有序端点序列 $segmentsTree$ ，每压入一个元素即会进行一次排序，维护其有序性

3. 扫描线从左至右进行扫描，每扫到一个端点，进行一次判别，判别规则如下： $O(n)$

若当前点 $s_{i.L}$ $s_{i . L}$ 为所在线段的左端点，则将该点所在线段 $s_i$ $s_{i}$ 压入 $segmentsTree$ $s e g m e n t s T r e e$ ，此时：
- 若 $segmentsTree$ 排序后，新压入的线段 $s_i$ 前面存在元素，则将该线段与其序列中前一个线段进行相交性检测 $O(logn)$
- 若 $segmentsTree$ 排序后，新压入的线段 $s_i$ 后面存在元素，则将该线段与其序列中后一个线段进行相交性检测
若当前点 $s_{i.R}$ $s_{i . R}$ 为所在线段的右端点，此时：
- 若点 $s_{i.R}$ 所在的线段 $s_i$ 前后均存在元素，则将该线段其序列中的前一个线段和后一个线段进行相交性检测
- 检测完毕后从 $segmentsTree$ 中移除线段 $s_i$

时间复杂度： $O(nlogn)$

2. 示例代码

2.1 import

import java.util.ArrayList;
import java.util.Collections;
import java.util.Comparator;
import java.util.TreeSet;
import primitives.Point;
import primitives.Segment;

2.2 SegmentsIntersect.class

2.2.1 成员

// 扫描线算法需要两个比较器：
// 一个用于比较某个X坐标中的两个线段（RB树中的用户），另一个用于对初始点进行“从左到右”排序。
private static SegmentsComparator segmentsComparator;
private static Comparator<Point> PointsComparatorX;

// 处理边界情况
private static boolean foundBoundaryCase;

// 记录一对相交的线段
private static Segment segm1, segm2;

2.2.2 内部类 SegmentsComparator.class

2.2.2.1 成员

1	private double x;

2.2.2.2 线段比较器 Comparator < Segment >

1	static class SegmentsComparator implements Comparator<Segment>;

如果返回值小于 0，说明比较结果是s1 < s2；
如果返回值等于 0，说明比较结果是s1 = s2；
如果返回值大于 0，说明比较结果是s1 > s2。

重写 compare

@Override
public int compare(Segment s1, Segment s2) {

    // 点在该X坐标中不可比较的情况
    if (x < s1.getLeft().getX() || x > s1.getRight().getX() ||
        x < s2.getLeft().getX() || x > s2.getRight().getX()) {
        return 0;
    }

    // 计算对应的X坐标的Y坐标
    double y1 = yForX(s1, x);
    double y2 = yForX(s2, x);

    // s1为竖直线
    if (Double.isNaN(y1)) {
        if(s1.getLeft().getY() >= y2 && s1.getRight().getY() <= y2) {
            // 一个边界条件
            segm1 = s1;
            segm2 = s2;
            foundBoundaryCase = true;
        }
        if (s1.getLeft().getY() < y2) {
            // P2 在 s1.Left上方（s1下，s2上）
            return -1;
        } else if (s1.getLeft().getY() > y2) {
            // P2 在 s1.Left下方，即在 s1.Right下方（s1上，s2下）
            return 1;
        } else {
            // 相交
            return 0;
        }
    // s2为竖直线 
    } else if (Double.isNaN(y2)) {
        if(s2.getLeft().getY() >= y1 && s2.getRight().getY() <= y1) {
            // 一个边界条件
            segm1 = s1;
            segm2 = s2;
            foundBoundaryCase = true;
        }
        if (s2.getLeft().getY() < y1) {
            // P1 在 s2.Left上方（s1上，s2下）
            return 1;
        } else if (s2.getLeft().getY() > y1) {
            // P1 在 s2.Left下方，即在 s2.Right下方（s1下，s2上）
            return -1;
        } else {
            // 相交
            return 0;
        }
    // P1 在 P2 下方
    } else if(y1 < y2) {
        return -1;
    // P1 在 P2 上方
    } else if (y1 > y2) {
        return 1;
    // P1 与 P2 重合，即扫描线扫描到了s1与s2的交点
    } else {
        if(s1 != s2) {
            // // 一个边界条件
            segm1 = s1;
            segm2 = s2;
            foundBoundaryCase = true;
        }
        return 0;
    }
}

可以进行比较的条件：

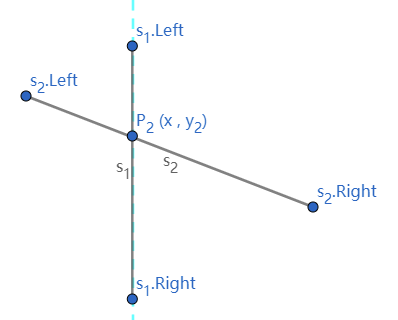
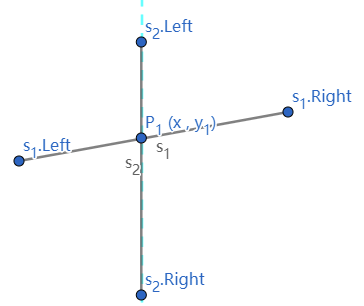
\begin{cases} s_1.left.x \le x \le s_1.right.x \\[2ex] s_2.left.x \le x \le s_2.right.x \end{cases}

令扫描线与线段 $s_1$ 和 $s_2$ 的交点分别为 $P_1(x, y_1)$ 和 $P_2(x, y_2)$

(Double.isNaN(y1))：扫描线扫到 $s_1$ $s_{1}$ 时，无法得到 $y_1$ $y_{1}$ ，即此时 $s_1$ $s_{1}$ 是一条竖直线
- 线段相交条件：(s1.getLeft().getY() >= y2 && s1.getRight().getY() <= y2)
  $s_1 == s_2$
$s_1.right.y \le y_2 \le s_1.left.y$
即 $P_2(x, y_2)$ $P_{2} (x, y_{2})$ 在点 $s_1.right$ $s_{1} . r i g h t$ 和 $s_1.left$ $s_{1} . l e f t$ 之间

(Double.isNaN(y2))：扫描线扫到 $s_2$ $s_{2}$ 时，无法得到 $y_2$ $y_{2}$ ，即此时 $s_2$ $s_{2}$ 是一条竖直线
- 线段相交条件：(s2.getLeft().getY() >= y1 && s2.getRight().getY() <= y1)
  $s_1 == s_2$
$s_2.right.y \le y_1 \le s_2.left.y$
即 $P_1(x, y_1)$ $P_{1} (x, y_{1})$ 在点 $s_2.right$ $s_{2} . r i g h t$ 和 $s_2.left$ $s_{2} . l e f t$ 之间

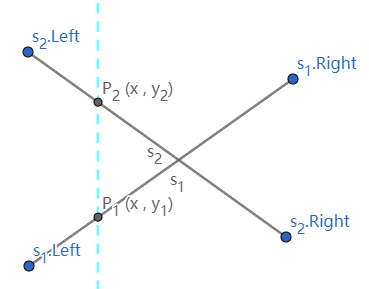
(y1 < y2)： $P_1(x, y_1)$ 在 $P_2(x, y_2)$ 下方
$s_1 < s_2$
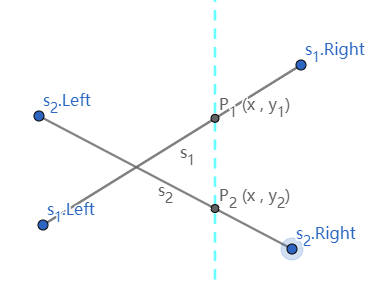
(y1 > y2)： $P_1(x, y_1)$ 在 $P_2(x, y_2)$ 上方
$s_1 > s_2$
(y1 = y2)： $P_1(x, y_1)$ 与 $P_2(x, y_2)$ 重合
此时 $P(x, y)$ 即为线段 $s_1$ 与 $s_2$ 的交点

2.2.2.3 其他方法

// 设置X坐标
public void setX(double x) {
    this.x = x;
}

// 通过线段的X坐标计算线段上的点的Y坐标。
private double yForX(Segment s, double x) {
    return (s.getRight().getX()*s.getLeft().getY() -
            s.getLeft().getX()*s.getRight().getY() -
            x*(s.getLeft().getY() - s.getRight().getY())) /
            (s.getRight().getX() - s.getLeft().getX());
}

2.2.3 端点比较器 Comparator < Point >

先比较两端点的 X 坐标（左小右大）
- $P_1.x < P_2.x \Rightarrow P_1 < P_2$
- $P_1.x > P_2.x \Rightarrow P_1 > P_2$
- $P_1.x = P_2.x$ $P_{1} . x = P_{2} . x$ : X 坐标相同时，即 竖直线 情况下，定义上的Left < Right
  - $(P_1-is Left)\land(P_2-is Right) \Rightarrow P_1 < P_2$
  - $(P_1-is Right)\land(P_2-is Left) \Rightarrow P_1 > P_2$
  - $[(P_1-is Left)\land(P_2-is Left)]\lor[(P_1-is Right)\land(P_2-is Right)]$ $[(P_{1} - i s L e f t) \land (P_{2} - i s L e f t)] \lor [(P_{1} - i s R i g h t) \land (P_{2} - i s R i g h t)]$ : 无法再通过 Left 与 Right 区分 $P_1$ $P_{1}$ 与 $P_2$ $P_{2}$ 的大小时，按Y坐标排序（下小上大）
    - $P_1.y < P_2.y \Rightarrow P_1 < P_2$
    - $P_1.y > P_2.y \Rightarrow P_1 > P_2$
若全部相同，则 $P_1 == P_2$

eg.

\begin{cases} P_1.x = P_2.x \\[2ex] [(P_1-is Left)\land(P_2-is Left)] \end{cases}

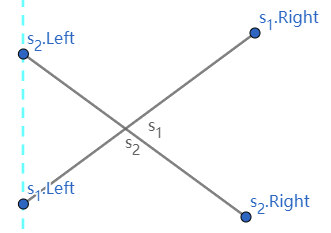
显然：此时 $P_1 < P_2$

// 比较器初始化
static {
    segmentsComparator = new SegmentsComparator();
    
    PointsComparatorX = new Comparator<Point>() {
        
        public int compare(Point p1, Point p2) {
            if (p1.getX() < p2.getX()) {
                return -1;
            } else if (p1.getX() > p2.getX()) {
                return 1;
            } else {
                // 如果X坐标相同，则"左点"应在"右点"之前
                if (p1.isLeft() && p2.isRight()) {
                    return -1;
                } else if (p1.isRight() && p2.isLeft()) {
                    return 1;
                } else {
                    // 如果仍然相同，则按Y坐标排序
                    if (p1.getY() < p2.getY()) {
                        return -1;
                    } else if (p1.getY() > p2.getY()) {
                        return 1;
                    } else {
                        return 0;
                    }
                }
            }
        }
    };
}

2.2.4 扫描线算法

public static boolean any(ArrayList<Segment> segments) {
    
    // 红黑树将支持时间复杂度为O（n * lg（n））的有序段集合
    TreeSet<Segment> segmentsTree = new TreeSet<Segment>(segmentsComparator);
    
    // 线段端点的数组，按其X坐标排序
    ArrayList<Point> points = new ArrayList<Point>();
    for (Segment s : segments) {
        points.add(s.getLeft());
        points.add(s.getRight());
    }
    Collections.sort(points, PointsComparatorX);

    Segment pSegm;
    foundBoundaryCase = false;
    
    for (Point p : points) { // 遍历点的有序列表
        
        // 设置将用于执行比较的X坐标（将扫描线移动至点 p）
        segmentsComparator.setX(p.getX());
        
        pSegm = p.getSegment();
        
        if (p.isLeft()) {
            
            // 插入
            segmentsTree.add(pSegm);
            
            if ((segmentsTree.lower(pSegm) != null &&
                    SegmentsIntersect.two(segmentsTree.lower(pSegm), pSegm))) {
                
                segm1 = segmentsTree.lower(pSegm);
                segm2 = pSegm;
                
                return true;
            }
            
            if ((segmentsTree.higher(pSegm) != null &&
                    SegmentsIntersect.two(segmentsTree.higher(pSegm), pSegm))) {
                
                segm1 = segmentsTree.higher(pSegm);
                segm2 = pSegm;
                
                return true;
            }
            
            if(foundBoundaryCase) {
                return true;
            }
        // p.isRight()
        } else { 
            
            if(segmentsTree.lower(pSegm) != null &&
                segmentsTree.higher(pSegm) != null &&
                SegmentsIntersect.two(segmentsTree.higher(pSegm),
                                        segmentsTree.lower(pSegm))) {
                
                segm1 = segmentsTree.higher(pSegm);
                segm2 = segmentsTree.lower(pSegm);
                
                return true;
            }
            
            segmentsTree.remove(pSegm);
        }
        
    }
    
    return false;
}

方法
public E lower(E e);	返回小于指定元素e的集合里最大的那个元素
public E higher(E e);	返回大于指定元素e的集合里最小的那个元素

1. 先将线段集合 segments 中的所有线段的两个端点压入端点集合 points 中

2. 对端点集合 points 进行排序，依据端点比较器 PointsComparatorX 所定义的比较规则，形成有序端点序列 points （排序后的数组）

3. 对端点序列 points 进行遍历（定义当前遍历的点为 p）

将扫描线移动至点 p ，线段指针 pSegm 指向 p 所在的线段
若 $p-isLeft$ $p - i s L e f t$ : 将线段 pSegm 压入有序线段序列 segmentsTree （红黑树）
- 若线段 pSegm 存在前一个线段 segmentsTree.lower(pSegm) ，则二者进行相交性检测
- 若线段 pSegm 存在后一个线段 segmentsTree.higher(pSegm) ，则二者进行相交性检测
若 $p-isRight$ : 当线段 pSegm 存在前一个线段 segmentsTree.lower(pSegm) 和后一个线段 segmentsTree.higher(pSegm) 时，线段 pSegm 前后两个线段进行相交性检测，之后再从线段序列 segmentsTree 中移除线段 pSegm

eg.

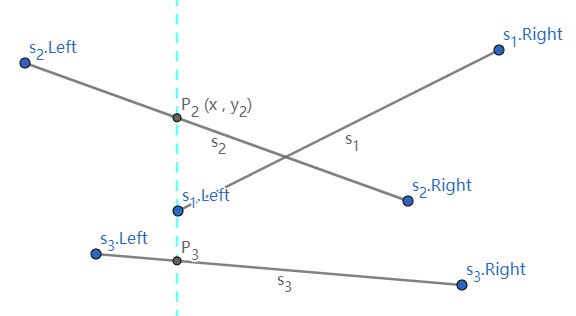
以图中为例：

初始阶段，线段集合 $$segments = {s_1,s_2,s_3}$$
端点集合 $$points = {s_{1.L},s_{1.R},s_{2.L},s_{2.R},s_{3.L},s_{3.R}}$$
对端点排序后，得到端点有序序列 $$points = {s_{2.L} < s_{3.L} < s_{1.L} < s_{2.R} < s_{3.R} < s_{1.R}}$$
以图中扫描线的位置为例，此时扫描线扫描到了点 $s_{1.L}$
此时segmentsTree.add(s1);

\begin{aligned} &segmentsTree = \{s_3 < s_2\}\\ \to &segmentsTree = \{s_3 < s_1 < s_2\} \end{aligned}

显然，此时有：
- (segmentsTree.lower(s1) == s3) : 对线段 $s_1$ 与 $s_3$ 进行相交性检测
- (segmentsTree.higher(s1) == s2) : 对线段 $s_1$ 与 $s_2$ 进行相交性检测

2.2.5 检测两线段是否相交

解析略

public static boolean two(Segment s1, Segment s2) {
    
    Point p1 = s1.getLeft();
    Point p2 = s1.getRight();
    Point p3 = s2.getLeft();
    Point p4 = s2.getRight();
    
    double d1 = direction(p3, p4, p1);
    double d2 = direction(p3, p4, p2);
    double d3 = direction(p1, p2, p3);
    double d4 = direction(p1, p2, p4);
    
    if (((d1 > 0 && d2 < 0) || (d1 < 0 && d2 > 0)) &&
        ((d3 > 0 && d4 < 0) || (d3 < 0 && d4 > 0))) {
        return true;
    } else if (d1 == 0 && onSegment(p3, p4, p1)) {
        return true;
    } else if (d2 == 0 && onSegment(p3, p4, p2)) {
        return true;
    } else if (d3 == 0 && onSegment(p1, p2, p3)) {
        return true;
    } else if (d4 == 0 && onSegment(p1, p2, p4)) {
        return true;
    } else {
        return false;
    }
}

private static double direction(Point p0, Point p1, Point p2) {
    return ((p2.getX() - p0.getX()) * (p1.getY() - p0.getY()) -
            (p2.getY() - p0.getY()) * (p1.getX() - p0.getX()));
}

private static boolean onSegment(Point pi, Point pj, Point pk) {
    return (Math.min(pi.getX(), pj.getX()) <= pk.getX() &&
            pk.getX() <= Math.max(pi.getX(), pj.getX()) &&
            Math.min(pi.getY(), pj.getY()) <= pk.getY() &&
            pk.getY() <= Math.max(pi.getY(), pj.getY()));
}

2.2.6 返回计算结果

public static ArrayList<Segment> intersectingSegments() {
    ArrayList<Segment> result = new ArrayList<Segment>();
    
    result.add(segm1);
    result.add(segm2);
    
    return result;
}

镜之国的爱丽丝

04 - 任意两线段是否相交 - 扫描线算法