06 - 点集的最小凸包 - march算法

1. 算法思路：

类似于选择排序，每次找到极角最小的点加入到点集 result 中，具体步骤见 2.2

时间复杂度 ：$O(n \cdot h)$
其中 $h$ 是凸包中顶点的数量，因此最坏的情况是 $O(n^2)$。

2. 示例代码：

2.1 import

import java.util.*;
import primitives.Point;
import primitives.Polygon;

2.2 march算法

public static Polygon Jarvis(ArrayList<Point> pointsList) {

    // 克隆点表，以便在算法期间更改。
    // 假设 pointsList.size >= 3。
    ArrayList<Point> points = (ArrayList<Point>)pointsList.clone();
    ArrayList<Point> result = new ArrayList<Point>();

    // 获取最左的最低点 - 作为凸包的第一个顶点 - O(n)
    Point p0 = getLowestPoint(points);
    result.add(p0);
    points.remove(p0);

    // 获取凸包的最后一个顶点 - O(n)
    // 即获取极角最大的点
    Point pE = points.get(0);
    Point candidate;
    for(int i = 1; i < points.size(); i++) {
        candidate = points.get(i);
        if(crossProduct(p0, candidate, pE) < 0) {
            pE = candidate;
        }
    }

    // 构建链 - O(h)
    Point next = null;
    Point last = p0;
    do {
        // ...每步扫描 O(n) 个点，因此总共进行 O(n*h) 个操作
        next = points.get(0);
        
        // 找极角最小的点
        // 如果极角相同，即三点共线，则 next 取离 P0 最远的
        for(int i = 1; i < points.size(); i++) {
            candidate = points.get(i);
            if (crossProduct(last, candidate, next) > 0 ||
                    crossProduct(last, candidate, next) == 0 &&
                    last.dist(candidate) > last.dist(next)) {
                next = candidate;
            }
        }
        
        result.add(next);
        points.remove(next);
        last = next;
        
    } while(next != pE);

    // 凸包已构建，现在按逆时针顺序(CCW)返回其顶点列表
    return new Polygon(result);
}

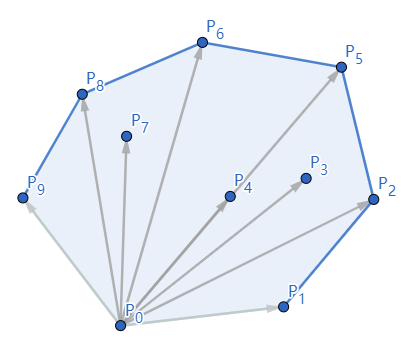
1. 先找最低点 $P_0$；

2. 对 points 进行遍历，找到极角最大点，即为 凸包的最后一个顶点 PE，该处为 $P_9$；

3. 再在 points 中找到以点 last 为轴，极角最小的点 next ，若极角相同，则取离 last 最远的；

4. 找到后，将极角最小的点 next 加入点集 result ，同时将 last 赋为 next ；（last 是变化的）

5. 重复进行步骤 3. ~ 4. 的操作，直至找到最后一个顶点 PE ，即 $P_9$ 。

points	result	last	next
$P_0$，$P_1$，$P_2$，$P_3$，$P_4$，$P_5$，$P_6$，$P_7$，$P_8$，$P_9$		NULL	NULL
$P_1$，$P_2$，$P_3$，$P_4$，$P_5$，$P_6$，$P_7$，$P_8$，$P_9$	$P_0$	$P_0$	NULL
$P_2$，$P_3$，$P_4$，$P_5$，$P_6$，$P_7$，$P_8$，$P_9$	$P_0$，$P_1$	$P_0$	$P_1$
$P_3$，$P_4$，$P_5$，$P_6$，$P_7$，$P_8$，$P_9$	$P_0$，$P_1$，$P_2$	$P_1$	$P_2$
$P_3$，$P_4$，$P_6$，$P_7$，$P_8$，$P_9$	$P_0$，$P_1$，$P_2$，$P_5$	$P_2$	$P_5$
$P_3$，$P_4$，$P_7$，$P_8$，$P_9$	$P_0$，$P_1$，$P_2$，$P_5$，$P_6$	$P_5$	$P_6$
$P_3$，$P_4$，$P_7$，$P_9$	$P_0$，$P_1$，$P_2$，$P_5$，$P_6$，$P_8$	$P_6$	$P_8$
$P_3$，$P_4$，$P_7$	$P_0$，$P_1$，$P_2$，$P_5$，$P_6$，$P_8$，$P_9$	$P_8$	$P_9$（跳出循环）

2.3 其他方法

2.3.1 叉积

// 计算叉积
private static double crossProduct(Point p0, Point p1, Point p2) {
    return (p1.getX() - p0.getX()) * (p2.getY() - p0.getY()) -
            (p2.getX() - p0.getX()) * (p1.getY() - p0.getY());
}

// 计算 p0p1 和 p0p2 的相对位置
private static boolean isLeftTurn(Point p0, Point p1, Point p2) {
    return (crossProduct(p0, p1, p2) > 0);
}

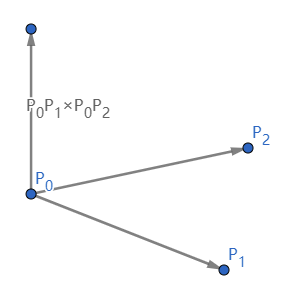
$P_0P_1 \times P_0P_2$

2.3.2 获得最低点

• 比较规则：
  • 先比较Y坐标
  • Y坐标相同时再比较X坐标

lowest-then-leftmost point（LTL）

private static Point getLowestPoint(ArrayList<Point> points) {
    Point result = points.get(0);

    // 候选点
    Point candidate;

    for (int i = 1; i < points.size(); i++) {
        candidate = points.get(i);
        
        if (candidate.getY() < result.getY() ||
                candidate.getY() == result.getY() && candidate.getX() < result.getX()) {
            result = candidate;
        }
    }
    
    return result;
}