镜之国的爱丽丝
0%

09 - 多边形的三角剖分 - 耳切法

发表于 更新于 分类于

1. 基本概念

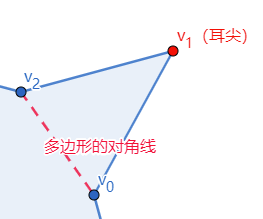
简单多边形的 耳朵（ear）：是指由连续顶点v0v_0，v1v_1 和 v2v_2 组成的内部不包含其他任意顶点的三角形。

在计算机几何术语中，v0v_0 与 v2v_2 之间的连线称之为多边形的对角线，点 v1v_1 称之为耳尖。

screenShot.png

  • 虽然你可以将耳尖放到三角形的任意一个顶点上，但是我们认为三角形包含一个耳尖。

  • 一个由四个顶点（或者更多）组成的多边形至少有两个不重叠的耳尖。

  • 这个特性提供了一个通过递归来解决三角化分割的方法。

  • 针对由 n 个顶点组成的多边形，找到其耳尖，移除唯一耳尖上的顶点，此时剩余顶点组成了一个 n-1 个顶点的简单多边形。

  • 我们重复这个操作直到剩余三个顶点。这样的话会产生一个复杂度为 O(n3)O(n^3) 的算法

  • 随着一些细节改进，耳朵消除可以在 O(n2)O(n^2) 的时间来完成。

2. 算法思路

1. 先将多边形使用双向链表存储，这样可以快速的移除耳朵，列表的构建复杂度是 O(n)O(n) ；

2. 遍历顶点寻找耳朵，对于每一个顶点 ViV_i 和围绕该顶点的三角形<vi−1,vi,vi+1><v_{i-1}, v_i, v_{i+1}>，(总长度为 NN ，所以 vn=v0v_n = v_0 ，并且 v−1=vn−1v - 1 = v_n - 1 )，测试其他顶点是否在当前三角形中，如果有一个顶点在三角形里面，则不是耳朵，只有都不在的情况，才算是找到一个耳朵。

  • 具体实现的时候我们可以考虑以下因素让这个算法更为高效。
  • 当发现有一个点在三角形里面的时候便可以开始放弃当前测试。
  • 一个凹拐角其两边的夹角大于180°，而一个凸拐角两边夹角小于180°。
  • 存储多边形的数据结构使用四个链表，具体使用数组而不是标准的动态需要分配合释放存储器的链表。
  • 多边形的顶点存储在在一个循环链表 vertices 中，凹顶点和凸顶点存储在线性表中，耳尖存储在一个循环列表 ears 中。

3. 一旦凸顶点和耳朵的链表构建成功，每次遍历都会移除一个耳朵。
假设当前 viv_i 是个耳朵并且被移除掉，那么边结构的相邻点 vi−1,vi+1v_{i-1}, v_{i+1} 则会发生变化：

  • 如果相邻点是 凸顶点 ，那么依旧保持凸点；
  • 如果相邻点是 耳朵 ，那么当 viv_i 被移除后则不一定能保持耳朵的状态；
  • 如果相邻点是 凹顶点 ，那么他则有可能变为一个凸点甚至是耳朵。

因此当移除顶点 viv_i 后，如果相邻点是凸点，则必须遍历相关顶点，通过遍历查看是否包含其他点，来测试它是否是一个耳朵。我们有 nn 个耳朵，每一次更新都会触发一个耳朵检测，每次过程中更新 O(n)O(n) ，所以移除进程的复杂度是 O(n2)O(n^2) 。

3. 示例代码

3.1 耳切法算法

计算给定多边形的梵高（耳切）三角剖分。
这个实现在 O(n2)O(n^2) 中运行，因为 ear 同时存储在一个单独的链表 ears 中，该列表每个步骤更新一次。

1
2
3
4
5
6
7
8
9
10
11
12
public static ArrayList<Triangle> fast(Polygon p) {
    
    ArrayList<Triangle> result = new ArrayList<Triangle>();
    
    VanGoghPolygon ap = new VanGoghPolygon(p);
    
    for(int i = 0; i < p.size() - 2; i++) {
        result.add(ap.removeEar());
    }
    
    return result;
}

3.2 梵高多边形类 VanGoghPolygon.class

3.2.1 import

1
2
3
import ru.dubov.primitives.Point;
import ru.dubov.primitives.Polygon;
import ru.dubov.primitives.Triangle;

3.2.2 成员

1
2
3
4
5
6
7
8
9
10
// 双链接循环链表存储顶点
private DoublyLinkedCyclicList<Point> vertices;

// Node<Point> 的双链接循环链表
// 存储的是指向 Node 的指针
// 修改时不会影响原顶点链表
private DoublyLinkedCyclicList<DoublyLinkedCyclicList<Point>.Node> ears;

// 是否顺时针
private boolean isClockwise;

3.2.3 构造方法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public VanGoghPolygon() {
    vertices = new DoublyLinkedCyclicList<Point>();
    ears = new DoublyLinkedCyclicList<DoublyLinkedCyclicList<Point>.Node>();
}

// 传入的多边形顶点倒序加入顶点的双链接循环链表 vertices
// 头插法的情况下 : P0 -> P1 -> P2 -> …… -> Pn
public VanGoghPolygon(Polygon p) {
    this();
    
    for (int i = p.size()-1; i >= 0; i--) {
        vertices.insert(p.get(i));
    }
    
    constructEarList();
}

3.2.4 移除耳朵

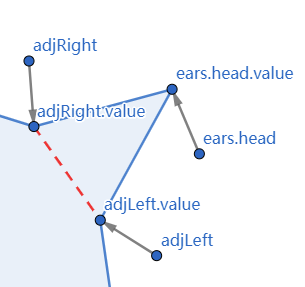
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
public Triangle removeEar() {
    
    // adjLeft -> ears.head -> adjRight
    DoublyLinkedCyclicList<Point>.Node adjLeft = ears.head().value.prev;
    DoublyLinkedCyclicList<Point>.Node adjRight = ears.head().value.next;
    
    Triangle ear = new Triangle(adjLeft.value,
            ears.head().value.value, adjRight.value);

    // 在顶点集 vertices 中删除
    ears.head().value.delete();

    // 在耳朵集 ears 中删除
    ears.head().delete();
    
    if (isConvex(adjLeft, isClockwise)) {
        // 再若移除 head 前 adjLeft 为耳朵
        // 则检查在移除 head 后 adjLeft 是否继续保持耳朵状态
        // 若 adjLeft 不再是耳朵，则从耳朵集 ears 中移除 adjLeft
        if (adjLeft == ears.head().prev.value) { 
            if (! isEar(ears.head().prev.value, isClockwise)) {
                ears.head().prev.delete();
            }
        // 再若移除 head 前 adjLeft 仅为凸点不是耳朵
        // 则检查在移除 head 后 adjLeft 是否成为新的耳朵
        } else if (isEar(adjLeft, isClockwise)) {
            ears.insert(adjLeft);
            ears.next();
        }
    }
    
    // ears.head 删除后，adjRight 现在变成了 head 
    if (isConvex(ears.head().value, isClockwise)) {
        // 再若移除 head 前 adjRight 为耳朵
        // 则检查在移除 head 后 adjRight 是否继续保持耳朵状态
        // 若 adjRight 不再是耳朵，则从耳朵集 ears 中移除 adjRight
        if (adjRight == ears.head().value) { 
            if (! isEar(ears.head().value, isClockwise)) {
                ears.head().delete();
            }
        // 再若移除 head 前 adjRight 仅为凸点不是耳朵
        // 则检查在移除 head 后 adjRight 是否成为新的耳朵
        } else if (isEar(adjRight, isClockwise)) {
            ears.insert(adjRight);
        }
    }
    
    return ear;
}

3.2.5 创建耳朵链表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public final void constructEarList() {
    DoublyLinkedCyclicList<Point>.Node cur = vertices.head();
    if (cur == null) return;
    
    isClockwise = isClockwise();
    
    // 构建 ear list - O(n^2)
    // 构建的链表是逆时针顺序从小到大排列
    cur = vertices.head().prev;
    do {
        if (isEar(cur, isClockwise)) {
            ears.insert(cur);
        }
        cur = cur.prev;
    } while(cur != vertices.head().prev);
}

3.2.6 判断凸点

1
2
3
4
private boolean isConvex(DoublyLinkedCyclicList<Point>.Node node, boolean isClockwise) {
    // 逆时针状态下左转是凸点，顺时针状态下右转是凸点
    return Point.isLeftTurn(node.prev.value, node.value, node.next.value) ^ isClockwise;
}

3.2.7 判断耳朵

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
// O(n)
private boolean isEar(DoublyLinkedCyclicList<Point>.Node node, boolean isClockwise) {
    // 凹点必定不是耳朵，因为耳朵的前提是凸点
    if (! isConvex(node, isClockwise)) {
        return false;
    }
    
    // 三角形：{Vi-1, Vi, Vi+1}
    Triangle tr = new Triangle(node.prev.value, node.value, node.next.value);
    
    // 对三点以外的其他点进行遍历，检测是否出现在三角形 tr 内部
    // 若存在某个其他点 cur 出现在三角形 tr 内部，则当前检测点 node.value 不是耳朵
    DoublyLinkedCyclicList<Point>.Node cur = vertices.head();
    do {
        if (tr.pointInside(cur.value)) return false;
        cur = cur.next;
    } while(cur != vertices.head());
    
    return true;
}

3.2.8 判断顺时针

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public boolean isClockwise() {
    double sum = 0;
    
    DoublyLinkedCyclicList<Point>.Node cur = vertices.head();
    
    // 计算该多边形的有向面积 sum ，面积大于 0 时，为顺时针标记
    do {
        sum += (cur.next.value.getX() - cur.value.getX())*
                (cur.next.value.getY() + cur.value.getY());
        
        cur = cur.next;
    } while(cur != vertices.head());
    
    return (sum > 0);
}

3.3 双链接循环链表 DoublyLinkedCyclicList < T >

3.3.1 成员

1
private Node head;

3.3.2 构造方法

1
2
3
public DoublyLinkedCyclicList() {
    head = null;
}

3.3.3 操作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
// 插入结点（头插法）
// head -> …… -> head.prev(last) 
// node -> head -> …… -> head.prev(last) 
// node(head) -> …… -> head.prev(last) 
public void insert(T value) {
    
    Node node = new Node(value);
    
    if (head == null) {
        head = node;
        
        head.next = head;
        head.prev = head;
        
        return;
    }
    
    head.prev.next = node;
    node.prev = head.prev;
    
    node.next = head;
    head.prev = node;
    
    head = node;
}

public void next() {
    head = head.next;
}

public void prev() {
    head = head.prev;
}

public Node head() {
    return head;
}

3.3.4 Node 类

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
public class Node {

    // 构造方法
    public Node() {
        next = prev = null;
    }

    public Node(T val) {
        next = prev = null;
        value = val;
    }
    
    // 将当前结点从链表中删除
    public void delete() {
    
        if (this.prev != null) {
            this.prev.next = this.next;
        }
        if (this.next != null) {
            this.next.prev = this.prev;
        }

        // 若为头结点，则指针 head 指向下一个结点
        if (head == this) {
            head = this.next;
        }
    }

    public Node next, prev;
    public T value;
}

参考资料

参考文章： 耳切法处理多边形三角划分 (有示例)