1. 矩阵的相关概念

m × n ：m 行 n 列
矩阵可看做是 向量的集合 ，具体划分要看是行向量表示法还是列向量表示法
- 行向量表示：m 个 n 维向量
- 列向量表示：n 个 m 维向量
矩阵可以表示一种变换，例如：
- 三维矩阵可以表示某个三维空间的线性变换
- 四维矩阵可以表示某个三维空间的仿射变换
- 四维矩阵可以表示某个三维空间向某个二维空间的透视投影

2. 使用矩阵表示向量的计算

2.1 把向量看做矩阵进行计算

一个n维向量可以看做一个 1 × n 的矩阵或者一个 n × 1 的矩阵；
其中 1 × n 的矩阵称为 行向量 ，n × 1 的矩阵称为 列向量 。

2.2 点乘

\vec{a} \cdot \vec{b} = \vec{a}^T \vec{b} = \begin{pmatrix} x_a & y_a & z_a \end{pmatrix} \begin{pmatrix} x_b \\ y_b \\ z_b \end{pmatrix} = x_a x_b + y_a y_b + z_a z_b

2.3 叉乘

可以通过矩阵变换的形式来进行叉乘，使用矩阵 $\bold{A}^{\times}$

\vec{a} \times \vec{b} = \bold{A}^{\times} \vec{b} = \begin{pmatrix} 0 & -z_a & y_a \\ z_a & 0 & -x_a \\ -y_a & x_a & 0 \end{pmatrix} \begin{pmatrix} x_b \\ y_b \\ z_b \end{pmatrix} = \begin{pmatrix} y_a z_b - y_b z_a \\ z_a x_b - z_b x_a \\ x_a y_b - x_b y_a \end{pmatrix}

该矩阵是 反对称 的：

(\bold{A}^{\times})^{T} = - \bold{A}^{\times}

易得：

\bold{A}^{\times} \vec{a} = \vec{0}

\bold{A}^{\times} \vec{b} = - \bold{B}^{\times} \vec{a}

通常，也有另一种形式

\vec{a} \times \vec{b} = \begin{vmatrix} \vec{i} & \vec{j} & \vec{k} \\ x_a & y_a & z_a \\ x_b & y_b & z_b \end{vmatrix} = (y_a z_b - y_b z_a)\vec{i} + (z_a x_b - z_b x_a)\vec{j} + (x_a y_b - x_b y_a)\vec{k}

3. 空间与变换

空间：用矩阵通过一组基向量表示张成的某个空间，是静态的状态。
- 其矩阵是表示一个空间的基向量的集合：
- 本质上是通过对 单位向量空间 $\bold{I}$ 进行该矩阵对应的变换之后，生成的一个新的向量空间；
- 即描述空间，实际上就是描述相对于给定参考点（通常是 单位向量空间 $\bold{I}$ ）的变换。
变换：用矩阵表示一个变换，是动态的过程。
- 可以对坐标系中的物体（点或者向量）进行变换；
- 也可以对坐标系本身，即直接对整个向量空间进行变换；
- 变换时要注意是行向量表示还是列向量表示，以此确定变换矩阵是左乘（列向量表示）还是右乘（行向量表示）。

3.1 空间

3.1.1 张量

该处提到的张量是物理意义上的，在数学上往往更倾向于称之为 张量场 ；并非数学意义上的张量。

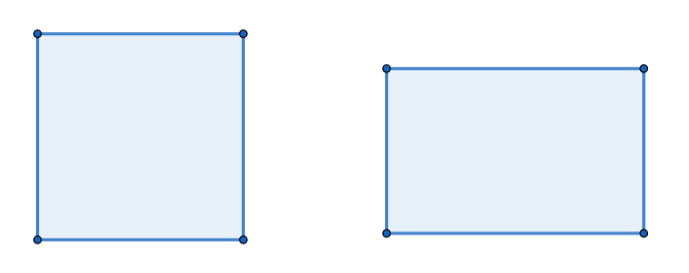
设有一个木块，在被施加某种载荷之后，发生了形变，从左变成了右。

显然，当边界可见的时候，可以很直观的看出该木块发生了什么样的形变。

但当我们在木块上无法确定这个木块的边界的时候，就需要用其他的方式来描述木块在这一过程中发生了何种形变。

有一种方式：

在木块上标记出一个小方格，并且使得小方格的边界正好与木块的边界平行；
当木块发生形变时，小方格的尺寸会随着木块一同变化；
通过观察小方格的形变，可以推出木块发生了何种形变。

（左图为变形前的木块和小方格，右图为变形后的木块和小方格。）

在材料力学中是这样定义这种形变的：

设木块原本的尺寸是 $L \times L$ ，它在均匀载荷作用下，
沿着横向(记为 $x$ 方向)变化了 $\Delta L_x$ ，
沿着纵向(记为 $y$ 方向)变化了 $\Delta L_y$ 。

我们将变化量与原长的比例记为：

\begin{cases} S_x = \Delta L_x / L \\[1.5ex] S_y = \Delta L_y / L \end{cases}

它们在材料力学上分别被称作其在 $x$ 方向和 $x$ 方向上的 正应变 。

由于木块的形变是处处均匀的，因此中央的小方格尺寸的正应变也分别为 $S_x$ 和 $S_y$ （尺寸变化的比例是一样的）。

于是，通过小方格的尺寸变化，就能推算出整个木板的形变状态了。

然而，在“看不到边界”的情况下，一般我们是无法直接标记出一个“边界正好与木块的边界平行”的小方格的，因此往往可能会是以下情况：

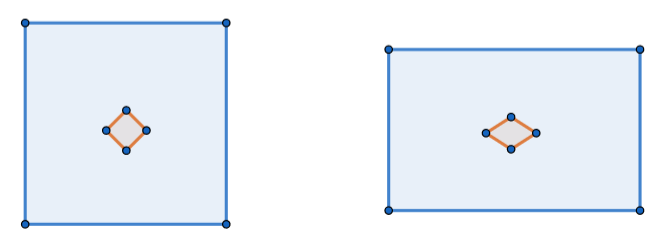
（左图为变形前的木块和小方格，右图为变形后的木块和小方格。）

可以看到，小方格不仅长度发生了变化，原本相互垂直的相邻两条边的夹角也发生了变化，不再是直角。

小方格相邻边的夹角变化，可称作 $xy$ 平面上的 切应变 ，记为 $S_{xy}$ 。
也就是说，如果小方格的边缘与木块边缘不平行，那么它会同时发生 正应变（尺寸变化） 和 切应变（夹角变化） 。

可以见到，同一种变换，在不同的坐标系下，表现出来的变换也不相同。
而张量可以直观地理解为这样一种量：

本身不随坐标系改变；
但是其表现出来的“投影”会随坐标系的改变而改变；
“投影”的变化满足某种统一的数学规律。

在木块形变的例子中我们知道，木块本身的形变状态与小方格的方向无任何关系，但是它在不同的小方格上却有着不同的体现。

在弹性力学中，木块本身的形变状态，就称作 应变张量 。

其本身不随坐标系（小方格）的改变而改变；

但应变张量在不同小方格上会表现出不同的形态，这在数学上就意味着，它在不同参考系中会有不同的“投影”。

“投影”写成矩阵形式就是：

S = \begin{bmatrix} S_x & S_{xy} \\ S_{xy} & S_y \end{bmatrix}

Note：当我们取的小方格边界不平行于木块边界的时候，应变张量的“投影”矩阵中 $S_{xy} \ne 0$ ,对应着 切应变 的出现。

参考文章：
https://zhuanlan.zhihu.com/p/53702458

3.1.2 向量空间

线性组合 ：表示一些向量的任意标量乘法之和， $Span\{ \vec{v_1},\cdots,\vec{v_p} \}$ 表示所有可以表示成 $\vec{v_1},\cdots,\vec{v_p}$ 的线性组合的向量集合。

若 $\vec{v_1},\cdots,\vec{v_p}$ 在向量空间 $\bold{V}$ 中，则 $Span\{ \vec{v_1},\cdots,\vec{v_p} \}$ 是 $\bold{V}$ 的一个 子空间 。
同时，我们称 $Span\{ \vec{v_1},\cdots,\vec{v_p} \}$ 是由 $\{ \vec{v_1},\cdots,\vec{v_p} \}$ 张成的子空间 。

用来表示作为某些向量线性组合的集合的子空间 $\bold{H}$ 。
若 $\bold{H} = Span\{ \vec{v_1},\cdots,\vec{v_p} \}$ ，我们可以把这个生成集中的向量 $\vec{v_1},\cdots,\vec{v_p}$ 看作 “柄” ，它们使我们能够掌握这个子空间 $\bold{H}$ 。
$\bold{H}$ 中无穷多个向量的运算经常被简化成生成集中的有限多个向量的运算。

列空间 ： $m \times n$ 矩阵的列空间（记为 $Col \bold {A}$ ）是由 $\bold {A}$ 的列的所有线性组合组成的集合，若 $A = [\vec{a_1},\cdots,\vec{a_n}]$ ，则 $Col \bold {A} = Span \{ \vec{a_1},\cdots,\vec{a_n} \}$ 。

基向量 ：通过一组向量描述一个子空间。
令 $\bold{H}$ 是向量空间 $\bold{V}$ 的一个子空间，若 $\bold{V}$ 中向量的指标集 $\mathcal{B} = \{ \vec{b_1},\cdots,\vec{b_p} \}$ 称为 $\bold{H}$ 的一个基，则其中必须：

$\mathcal{B}$ 是一线性无关集 .
由 $\mathcal{B}$ 生成的子空间与 $\bold{H}$ 相同，即 $\bold{H} = Span\{ \vec{b_1},\cdots,\vec{b_p} \}$ .

eg ：
以三维空间为例，我们使用 $\vec{i}$ ， $\vec{j}$ ， $\vec{k}$ 这三个 两两正交 的 单位向量 组成的矩阵，用来表示由该向量组构建的一个坐标系为基的三维空间：

\hat{i} = \begin{bmatrix} x_i \\ y_i \\ z_i \end{bmatrix}, \hat{j} = \begin{bmatrix} x_j \\ y_j \\ z_j \end{bmatrix}, \hat{k} = \begin{bmatrix} x_k \\ y_k \\ z_k \end{bmatrix}

那么对应的 列空间 $Col \bold{F}$ 为：

\bold{F} = \begin{bmatrix} \hat{i} & \hat{j} & \hat{k} \end{bmatrix} = \begin{bmatrix} \begin{array}{c:c:c} x_i & x_j & x_k \\ y_i & y_j & y_k \\ z_i & z_j & z_k \\ \end{array} \end{bmatrix}

NOTE：一般选择基的时候，常倾向于选择一组经过 标准正交化 的向量作为基向量，因为这样的基构成的矩阵是 标准正交矩阵 ，可以很快速的求出该矩阵的逆：

\bold{F}^{-1} = \bold{F}^{T}

这样便可以更快速的确定一个向量 $\vec{r}$ 在 列空间 $Col \bold{F}$ 上的线性表示

3.2 变换

3.2.1 向量表示

假设集合 $\mathcal{B} = \{ \vec{b_1},\cdots,\vec{b_p} \}$ 是 $\bold{V}$ 的一个基， $\vec{x}$ 在 $\bold{V}$ 中， $\vec{x}$ 相对于基 $\mathcal{B}$ 的坐标（或 $\vec{x}$ 的 $\mathcal{B-}$ 坐标）是使得 $\vec{x} = c_1 \vec{b_1} + \cdots + c_n \vec{b_n}$ 的权 $c_1, \cdots ,c_n$ .
若 $(c_1, \cdots ,c_n)$ 是 $\vec{x}$ 的 $\mathcal{B-}$ 坐标，则 $\Bbb{R}^n$ 中的向量

[\vec{x}]_B = \begin{bmatrix} c_1 \\ \vdots \\ c_n \end{bmatrix}

是 $\vec{x}$ （相对于 $\mathcal{B}$ ）的坐标向量 ，或 $\vec{x}$ 的 $\mathcal{B-}$ 坐标向量 ，映射 $\vec{x} \mapsto [\vec{x}]_B$ 称为 （由 $\mathcal{B}$ 确定的）坐标映射 .

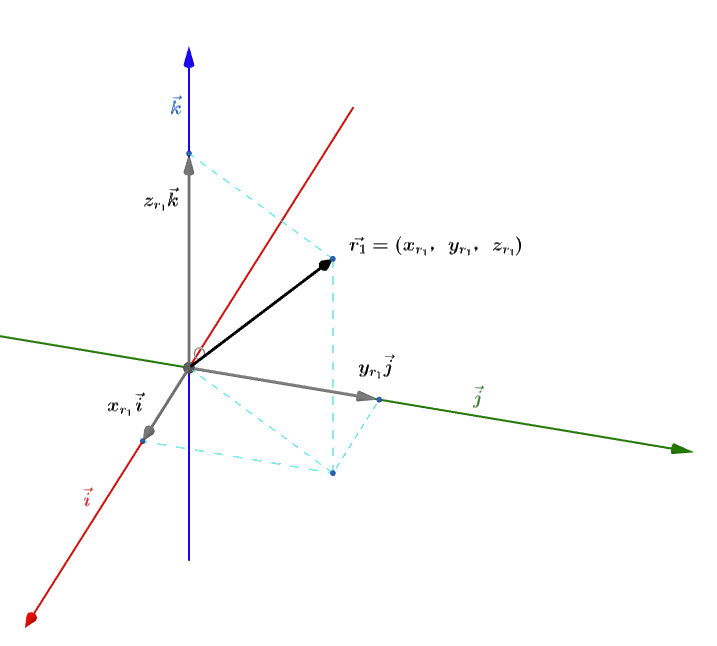
三维空间中，三维向量的三个分量，即是三维空间中的三个基向量的分量，将其合并后便构成该向量；
当我们用一个数字的序列描述一个向量时，往往需要依赖于一组 标准正交基 进行描述；
该空间中的任意向量，均可由这三个基向量 线性表示
以列向量表示法为例：

\vec{r} = \bold{F}\vec{r_1} = \begin{bmatrix} \hat{i} & \hat{j} & \hat{k} \end{bmatrix} \begin{bmatrix} x_{r_1} \\ y_{r_1} \\ z_{r_1} \end{bmatrix} = x_{r_1}\hat{i} + y_{r_1}\hat{j} + z_{r_1}\hat{k}

展开之后：

\vec{r} = \bold{F}\vec{r_1} = x_{r_1}\hat{i} + y_{r_1}\hat{j} + z_{r_1}\hat{k} = \begin{bmatrix} x_{r_1}x_i + y_{r_1}x_j + z_{r_1}x_k \\ x_{r_1}y_i + y_{r_1}y_j + z_{r_1}y_k \\ x_{r_1}z_i + y_{r_1}z_j + z_{r_1}z_k \end{bmatrix} = \begin{bmatrix} x_{r} \\ y_{r} \\ z_{r} \end{bmatrix}

同时也有：

\vec{r_1} = \bold{F^{-1}}\vec{r}

不难发现，其中隐藏有一个 坐标系变换 的过程，是从以 单位列空间 $Col \bold{I}$ 为基的坐标系，变换为以 列空间 $Col \bold{F}$ 为基的坐标系；不过虽然坐标系发生了变换，但是向量 $\vec{r}$ 没有跟着发生变换，因此其三个分量会对应的发生变化。
NOTE：注意，这里不是 物体变换

3.2.2 向量向坐标轴的投影

可以用投影的角度，这里将向量 $\vec{r}$ 投影到列空间 $Col \bold{F}$ 上，将三条基向量以 行向量 的形式组成矩阵

\vec{r_1} = \bold{F^{T}} \vec{r} = \begin{bmatrix} x_i & y_i & z_i \\ \hdashline x_j & y_j & z_j \\ \hdashline x_k & y_k & z_k \end{bmatrix} \vec{r} = \begin{bmatrix} \hat{i}^T \\[1.5ex] \hat{j}^T \\[1.5ex] \hat{k}^T \end{bmatrix} \vec{r} = \begin{bmatrix} \hat{i}^T \cdot \vec{r} \\[1.5ex] \hat{j}^T \cdot \vec{r} \\[1.5ex] \hat{k}^T \cdot \vec{r} \end{bmatrix} = \begin{bmatrix} x_{r_1} \\[1.5ex] y_{r_1} \\[1.5ex] z_{r_1} \end{bmatrix}

其中有：

分量	含义
$\hat{i}^T \cdot \vec{r}$	向量 $\vec{r}$ 在基向量 $\hat{i}$ 上的投影
$\hat{j}^T \cdot \vec{r}$	向量 $\vec{r}$ 在基向量 $\hat{j}$ 上的投影
$\hat{k}^T \cdot \vec{r}$	向量 $\vec{r}$ 在基向量 $\hat{k}$ 上的投影

由于矩阵 $\bold{F}$ 是 标准正交矩阵 ，于是有 $\bold{F}^{-1} = \bold{F}^{T}$ ，那么：

\vec{r_1} = \bold{F^{T}} \vec{r} = \bold{F^{-1}} \vec{r}

在 列向量 表示的情况下，将基向量在矩阵中按行表示，可以构成一个向该向量空间进行投影的矩阵。

NOTE ：
投影时，首先需要对描述坐标轴的向量进行 标准化 （可以不进行正交化）。

当矩阵是由某个向量空间的基向量组构建的时候，其中仅仅只包含坐标轴方向的相关信息，坐标轴的长度信息是无意义的，因此对其进行标准化时，不会影响对原空间的表示；
同时，在投影前，又必须对描述待投影的坐标的向量进行标准化，因为只有对单位向量的点乘结果才与其投影分量的结果数值相等；
当然，若投影的坐标轴向量不是单位向量，便需要有一个除以向量模的操作，具体回见向量点乘的几何意义。

3.2.3 向量的坐标系变换

向量的坐标系变换本质上可以看做是先将相对于 $\bold{F_1}$ 的坐标向量 $\vec{r_1}$ 还原到相对于 $\bold{I}$ 的坐标向量 $\vec{r}$ ，然后再将其投影到 $\bold{F_2}$

从 列空间 $\bold{F_1}$ 变换到 列空间 $\bold{F_2}$ ，同时不妨设向量 $\vec{r}$ 在两个向量空间中的线性表示分别为向量 $\vec{r_1}$ 与 $\vec{r_2}$ ，那么有以下关系：

3.2.3.1 坐标系变换：

具体有以下过程：

\vec{r_1} \xmapsto[]{\bold{F_1}} \vec{r} \xmapsto[]{\bold{F_2^{T}}} \vec{r_2}

这个过程具体有两个步骤：

\vec{r_2} = \bold{F_2^{T}} \bold{F_1} \vec{r_1}

先将 $\vec{r_1}$ 向量跟着向量空间 $\bold{F_1}$ 一同变化，此时便能获得 $\vec{r_1}$ 在源空间上的投影 $\vec{r}$ ；
之后将向量 $\vec{r}$ 投影到坐标系 $\bold{F_2}$ 上，投影时坐标系按行组成矩阵，即 $\bold{F_2^{T}}$ ，获得向量 $\vec{r_2}$ ；

3.2.3.2 与之等价的物体变换：

在 坐标系变换 之后，若其中的物体没有跟着进行变换，其分量必然会发生变化，而这种变化我们同样可以将其等效为是一种 物体变换 ：

\vec{r_1} \xmapsto[]{\bold{M}} \vec{r_2}

将该变换写成另一种形式：

\bold{M}\vec{r_1} = \vec{r_2}

由上面讨论过的等式：

\begin{aligned} &\bold{I}\vec{r} = \bold{F_1}\vec{r_1} = \bold{F_2}\vec{r_2} \\ \Rightarrow &\bold{F_2}^{-1}\bold{F_1}\vec{r_1} = \vec{r_2} \end{aligned}

NOTE：不难发现，正交坐标系 变换的量与其等价的物体变换的量是刚好相反的，反映在变换矩阵上就是，物体向某坐标系投影的坐标系矩阵（按行解读） 和与其等价的 物体变换的变换矩阵（按列解读） 是刚好互逆的。

镜之国的爱丽丝

02 - 矩阵基础