1. 射线
1.1 定义
- 数学定义:
射线 是直线的“一半”,有一个起点并向一个方向无限延伸。
- 计算几何中的定义:
射线 是一个有向线段。
射线有起点和终点。
一个射线定义了一个 位置 ,一个 有限长度 和一个 方向 。(除非射线长度为零)
任何射线都定义了包含这个射线的一条直线和线段。
1.2 两点表示法
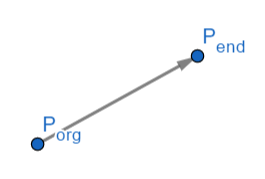
使用两个端点,起点 Porg 和终点 Pend
1.3 射线的参数形式
⎩⎪⎨⎪⎧x(t)=x0+tΔxy(t)=y0+tΔyz(t)=z0+tΔz
使用向量表示:
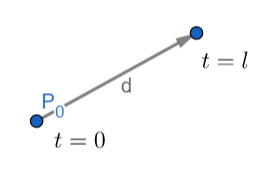
p(t)=p0+td
其中单位向量 d 表示射线方向,设射线的长度为 l ,参数 t∈[0,l],那么射线的终点则为:
p(l)=p0+ld
1.4 2D直线表示法
该表示法仅适用于二维空间
{ax+by=dp⋅n=dis
- 令指向点 Pi 的向量为 pi ,向量 pi 在沿着方向 n 的投影的长度为 dis ,该直线 L 即为所有满足该表达式的点 Pi 的集合;
- 过原点 O 向直线 L 做一条垂线,可知该垂线过点 M(a,b) 。
NOTE:图中点 M(a,b) 在直线 L 上,即有 ∥∥∥OM∥∥∥=dis=a2+b2 ,但是一般情况下点 M(a,b) 不一定在直线 L 上。
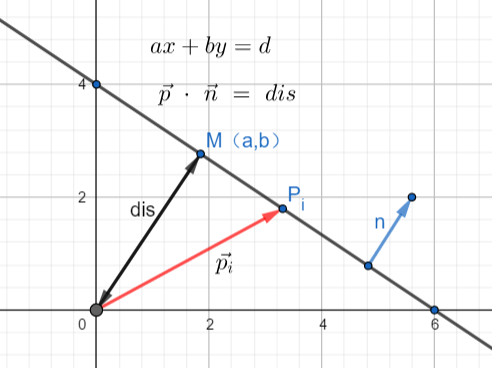
n 是垂直于直线的单位向量,dis 给出了原点到直线的 有符号距离 ,这个距离是在垂直于直线的方向(平行于 n)上度量的
- 有符号距离:如果直线与标准向量 n 代表的点在原点的同一侧,则 dis 为正;当 dis 增大时,直线会沿着方向 n 平移
1.4.1 点到直线的距离
点 p(x0,y0) 到直线 L 的距离为:
dis(p,L)=a2+b2∣ax0+by0−d∣
1.4.2 不同表示方法的转换
{ax+by=dp⋅n=dis
其中有以下关系:
⎩⎪⎪⎪⎨⎪⎪⎪⎧n=a2+b2(a,b)=(a2+b2a,a2+b2b)dis=a2+b2d
同时,
⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧a=b=d=
2. 示例代码
2.1 成员变量
1
2
3
4
5
6
7
8
9
10
11
|
Vector3 start;
Vector3 dir;
float len;
float t;
|
2.2 构造函数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
Ray3::Ray3()
{
st = Vector3(0, 0, 0);
dir = Vector3(0, 0, 0);
len = 0;
t = 1;
}
Ray3::Ray3(const Vector3& inSt, const Vector3& inDir)
{
st = Vector3(inSt.x, inSt.y, inSt.z);
dir = Vector3(inDir.x, inDir.y, inDir.z);
dir.normalize();
len = vectorMag(dir);
t = 1;
}
Ray3::Ray3(const Vector3& inSt, const Vector3& inDir, float inLen)
{
st = Vector3(inSt.x, inSt.y, inSt.z);
dir = Vector3(inDir.x, inDir.y, inDir.z);
dir.normalize();
this->len = inLen;
t = 1;
}
|


