1. 定义
1.1 平面定义 —— 隐式定义
- 可以用类似于定义 2D 直线的方法来定义平面。
- 平面的隐式定义由所有满足平面方程的点 p=(x,y,z) 给出
平面方程的两种表示法:
{ax+by+cz=dp⋅n=dis
其中有以下关系:
⎩⎪⎪⎪⎨⎪⎪⎪⎧n=a2+b2+c2(a,b,c)=(a2+b2+c2a,a2+b2+c2b,a2+b2+c2c)dis=a2+b2+c2d
- 向量 n 即为平面的法向量,垂直于整个平面
同时,
⎩⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎧a=b=c=d=
1.2 平面定义 —— 三点定面
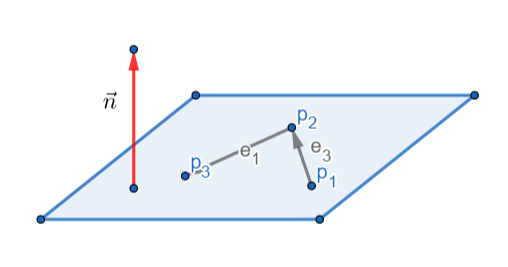
- 通过平面上的三个点 p1 , p2 和 p3 来计算 n 和 dis ;
- 右手坐标系下,当从平面正面看时,三个点 p1 , p2 和 p3 逆时针列出。
<1> 求向量 n :
⎩⎨⎧e3=p2−p1e1=p3−p2⇒n=∥e3×e1∥e3×e1
<2> 求 dis :
dis=p1⋅n=p2⋅n=p3⋅n
1.3 多于三个点的“最佳”平面
从一组三个以上的点集出平面方程,这种点集最常见的例子就是多边形的顶点,这些顶点绕多边形 逆时针 列出。
- 会遇到的问题
- 多边形是凹的,这些点恰好在凹处,从而构成了顺时针,导致法向量方向错误;
- 可能由于浮点数精确问题或者错误的生成多边形的方法,使得多边形的顶点可能会出现不共面的情况。
因此需要从点集中求出“最佳”,该平面应综合考虑所有的点:
p1=[x1y1z1]p1=[x2y2z2]⋮p1=[xn−1yn−1zn−1]p1=[xnynzn]
1.3.1 最佳平面的法向量 n :
nx=(z1+z2)(y1−y2)+(z2+z3)(y2−y3)+⋯+(zn−1+zn)(yn−1−yn)+(zn+z1)(yn−y1)ny=(x1+x2)(z1−z2)+(x2+x3)(z2−z3)+⋯+(xn−1+xn)(zn−1−zn)+(xn+x1)(zn−z1)nz=(y1+y2)(x1−x2)+(y2+y3)(x2−x3)+⋯+(yn−1+yn)(xn−1−xn)+(yn+y1)(xn−x1)
若设 pn+1=p1 ,使用求和符号,则有:
nx=i=1∑n(zi+zi+1)(yi−yi+1)ny=i=1∑n(xi+xi+1)(zi−zi+1)nz=i=1∑n(yi+yi+1)(xi−xi+1)
若需要限制 n 必须为单位向量,则该向量必须正则化。
1.3.2 最佳平面的距离 dis :
dis=n1i=1∑n(pi⋅n)=n1(i=1∑npi)⋅n
1.3.2 计算点集的最佳平面:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| Vector3 computeBestFitNormal (const Vector3 v[], int n)
{
Vector3 result = kZeroVector;
const Vector3 *p = &v[n-1];
for(int i = 0; i < n; ++i)
{
const Vector3 *c = &v[i];
result.x += (p->z + c->z) * (p->y - c->y);
result.y += (p->x + c->x) * (p->z - c->z);
result.z += (p->y + c->y) * (p->x - c->x);
p = c;
}
result.normalize();
return result;
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| float computeBestDis (const Vector3 v[], int n, const Vector3& normalVec)
{
float disRes = 0;
Vector3 sumVec = kZeroVector;
const Vector3 *p = &v[n-1];
for(int i = 0; i < n; ++i)
{
sumVec += *p;
}
disRes = (sumVec * normalVec) / n;
return disRes;
}
|
1.4 点到平面的距离
1.4.1 函数式 ax+by+cz=d
点 q(x0,y0,z0) 到平面 P 的距离为:
dis(q,P)=a2+b2+c2∣ax0+by0+cz0−d∣
1
2
3
4
5
6
| float computetDis (float a, float b, float c, float d, const Vector3& q)
{
float disRes = fabs(a * q.x + b * q.y + c * q.z - d) / sqrt(a*a + b*b + c*c);
return disRes;
}
|
1.4.2 点和法向量表达式 p⋅n=dis
设想一个平面和一个不在平面上的点 q 。平面上存在一个点 p ,它到 q 的距离最短。显然,从 p 到 q 的向量垂直于平面,且形式为 a⋅n 。
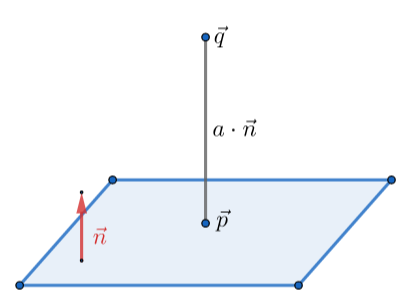
p+a⋅n(p+a⋅n)⋅np⋅n+a⋅n⋅ndis+aa=q=q⋅n=q⋅n=q⋅n=q⋅n−dis
计算任意点到平面的有符号距离
1
2
3
4
5
6
| float computetDis (float dis, const Vector3& normalVec, const Vector3& q)
{
float disRes = q * normalVec - dis;
return disRes;
}
|

