镜之国的爱丽丝
0%

01 - 最近点

发表于 更新于 分类于 ，

1. 2D 隐式直线上的最近点

考虑 2D 中的直线 LL ， LL 由所有满足 p⋅n=d\bold{p} \cdot \bold{n} = d 的点 p\bold{p} 组成。

其中 n\bold{n} 是单位向量，目标是对任意点 q\bold{q} ，找出直线 LL 上距 q\bold{q} 距离最短的点 q′\bold{q'} ，它是 q\bold{q} 投影到 LL 上的结果。

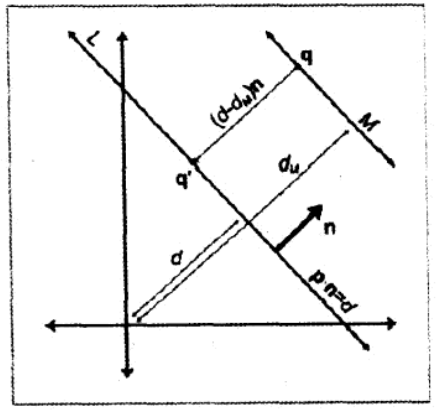
screenShot.png

画一条经过 q\bold{q} 并平行于 LL 的辅助线 MM ，设 nM\bold{n_M} 和 dMd_M 分别为直线方程的法向量和距离原点的距离。

由于 LL 和 MM 平行，所以他们法向量相等：nM=n\bold{n_M} = \bold{n} 。

又 q\bold{q} 在 MM 上，因此 dM=q⋅nd_M = \bold{q} \cdot \bold{n} 。

MM 到 LL 的 有符号距离 为：d−dM=d−q⋅nd - d_M = d - \bold{q} \cdot \bold{n} 。

  • 这个距离显然等于 q\bold{q} 与 q′\bold{q'} 之间的距离（如果结果只需要距离而不是 q′\bold{q'} 的值，到这里就可以停止计算了）。

为了计算 q′\bold{q'} ，只需要将 q\bold{q} 沿着 n\bold{n} 的方向位移一定距离：

q′=q+(d−dM)n=q+(d−q⋅n)n\begin{aligned} \bold{q'} &= \bold{q} + (d - d_M) \bold{n} \\ &= \bold{q} + (d - \bold{q} \cdot \bold{n}) \bold{n} \end{aligned}

2. 参数射线上的最近点

在 2D 或 3D 中的参数射线 R：p(t)=porg+tdR ：\bold{p}(t) = \bold{p_{org}} + t\bold{d}

其中 d\bold{d} 是单位向量，参数 tt 在 0 到 ll 间变化， ll 是 RR 的长度。
对一给定点 q\bold{q} ，需要找出在 RR 上离 q\bold{q} 最近的点 q′\bold{q'} 。

设 v\bold{v} 为 porg\bold{p_{org}} 到 q\bold{q} 的向量。我们希望得到 v\bold{v} 在 d\bold{d} 上的投影，或 v\bold{v} 平行于 d\bold{d} 的部分。

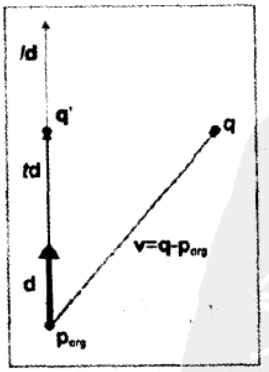
screenShot.png

点乘 v⋅d\bold{v} \cdot \bold{d} 的结果就是满足 p(t)=q′\bold{p}(t) = \bold{q'} 的 tt 值。

t=d⋅v=d⋅(q−porg)q′=p(t)=porg+td=porg+(d⋅(q−porg))d\begin{aligned} t &= \bold{d} \cdot \bold{v} \\ &= \bold{d} \cdot (\bold{q} - \bold{p_{org}}) \\[2ex] \bold{q'} &= \bold{p}(t) \\ &= \bold{p_{org}} + t \bold{d} \\ &= \bold{p_{org}} + (\bold{d} \cdot (\bold{q} - \bold{p_{org}}))\bold{d} \end{aligned}

等式 p(t)\bold{p}(t) 求得了在包含 RR 的直线上距 q\bold{q} 最近的点。

如果 t<0t < 0 或 t>lt > l ，则 p(t)\bold{p}(t) 不在 RR 的范围内。

这种情况下， RR 上距 q\bold{q} 最近的点是原点（如果 t<0t < 0 ）或者终点（如果 t>lt > l ）。

如果射线的定义是 tt 从 0 到 1 变化， d\bold{d} 不必是单位向量。那么在计算 tt 值必须除以 d\bold{d} 的模：

t=d⋅(q−porg)∥d∥t = \cfrac{\bold{d} \cdot (\bold{q} - \bold{p_{org}})}{\Vert {\bold{d}} \Vert}

3. 平面上的最近点

平面 p\bold{p} 的标准的隐式：p⋅n=d\bold{p} \cdot \bold{n} = d ；

其中 n\bold{n} 为单位向量。给定一点 q\bold{q} ，我们想要找到点 q′\bold{q'} ，它是 q\bold{q} 在 p\bold{p} 上的投影；

q′\bold{q'} 就是 p\bold{p} 上离 q\bold{q} 最近的点。

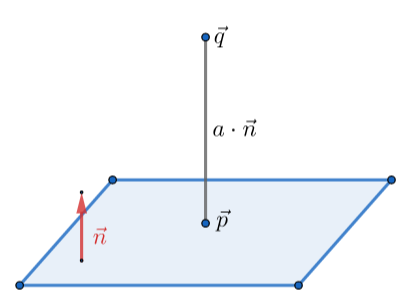
screenShot.png

见 《05 - 平面类》 1.4 点到平面的距离：

a=q⋅n−da = \bold{q} \cdot \bold{n} - d

计算 q′\bold{q'} ，只需要在 n\bold{n} 的方向上平移一段距离：

q′=q−a⋅n=q+(d−q⋅n)⋅n\begin{aligned} \bold{q'} &= \bold{q} - a \cdot \bold{n} \\ &= \bold{q} + (d - \bold{q} \cdot \bold{n}) \cdot \bold{n} \end{aligned}

4. 圆或球上的最近点

已知 2D 中的点 q\bold{q} 和圆心为 c\bold{c} 、半径为 rr 的圆（也适用于 3D 中的球体）。
目标是找到一点 q′\bold{q'} ，它是圆上离 q\bold{q} 最近的点。

设 d\bold{d} 为从 q\bold{q} 指向 c\bold{c} 的向量。该向量和圆相较于 q′\bold{q'} 。设 b\bold{b} 为从 q\bold{q} 指向 q′\bold{q'} 的向量。

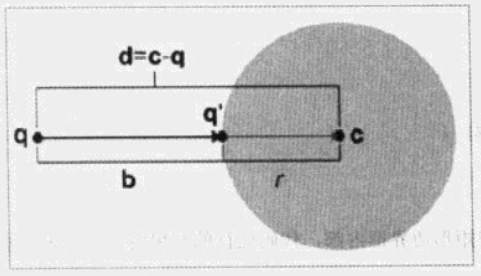
screenShot.png

显然：

∥b∥=∥d∥−r\Vert {\bold{b}} \Vert = \Vert {\bold{d}} \Vert - r

可得：

b=∥d∥−r∥d∥d\bold{b} = \cfrac{\Vert {\bold{d}} \Vert - r}{\Vert {\bold{d}} \Vert} \bold{d}

将此位移加至 q\bold{q} 上，则可将它投影到圆上：

q′=q+b=q+∥d∥−r∥d∥d\begin{aligned} \bold{q'} &= \bold{q} + \bold{b} \\ &= \bold{q} + \cfrac{\Vert {\bold{d}} \Vert - r}{\Vert {\bold{d}} \Vert} \bold{d} \end{aligned}

退化情况 ：

  • 若 ∥d∥<r\Vert {\bold{d}} \Vert < r，那么 q\bold{q} 在圆内部；
  • 若 q=c\bold{q} = \bold{c} ，那么 q\bold{q} 在圆心。

5. AABB 上的最近点

设 BB 是由极值点 pmin\bold{p_{min}} 和 pmax\bold{p_{max}} 定义的 AABB 。

对任意点 q\bold{q} 均可计算出在 BB 上距离 q\bold{q} 最近的点 q′\bold{q'} 。

主要思路是按一定顺序沿着每条轴将 q\bold{q} “推向” BB 。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
//---------------------------------------------------------------------------
// AABB3::closestPointTo
//
// 返回 AABB 上的最近点

Vector3	AABB3::closestPointTo(const Vector3& p) const {

	// 在每一维上将 p "Push" 进入矩形边界框

	Vector3 r;

	if (p.x < min.x) {
		r.x = min.x;
	}
	else if (p.x > max.x) {
		r.x = max.x;
	}
	else {
		r.x = p.x;
	}

	if (p.y < min.y) {
		r.y = min.y;
	}
	else if (p.y > max.y) {
		r.y = max.y;
	}
	else {
		r.y = p.y;
	}

	if (p.z < min.z) {
		r.z = min.z;
	}
	else if (p.z > max.z) {
		r.z = max.z;
	}
	else {
		r.z = p.z;
	}

	// 返回

	return r;
}