04 - 射线和平面的相交性检测

射线和平面的相交性检测

令射线的参数定义为：

$\bold{p}(t) = \bold{p_0} + t \bold{d}$

平面以标准形式定义：

$\bold{p} \cdot \bold{n} = dis$

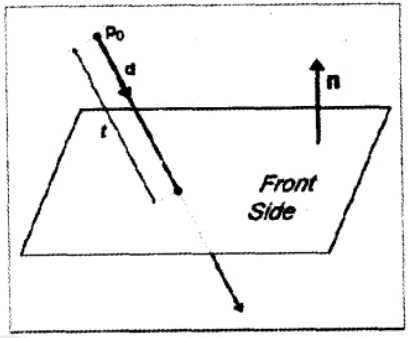
暂不需要 $\bold{n}$ 和 $\bold{d}$ 为单位向量

解得相交点的 $t$ 值，暂设射线的长度无限。

$\begin{aligned} (\bold{p_0} + t \bold{d}) \cdot \bold{n} &= dis \\ \bold{p_0} \cdot \bold{n} + t \bold{d} \cdot \bold{n} &= dis \\ t \bold{d} \cdot \bold{n} &= dis - \bold{p_0} \cdot \bold{n} \end{aligned}$

解得：

$t = \cfrac{dis - \bold{p_0} \cdot \bold{n}}{\bold{d} \cdot \bold{n}}$

NOTE：

• 如果射线和平面相互平行，分母 $\bold{d} \cdot \bold{n} = 0$ ，则它们之间没有交点；
• 此时仅考虑平面的正面相交的情况，此时仅当射线的方向和平面的法向量相反时才有交点，此时 $\bold{d} \cdot \bold{n} < 0$ ；
• 若 $t$ 超出了取值范围，说明射线和平面不相交。