07 - 射线和 圆_球 的相交性检测

射线和 圆_球 的相交性检测

由于可以在包含射线和球心的平面中进行检测，所以先讨论2D中射线和圆的相交性检测，该检测的方法也适用于3D中射线和球之间的相交性检测。

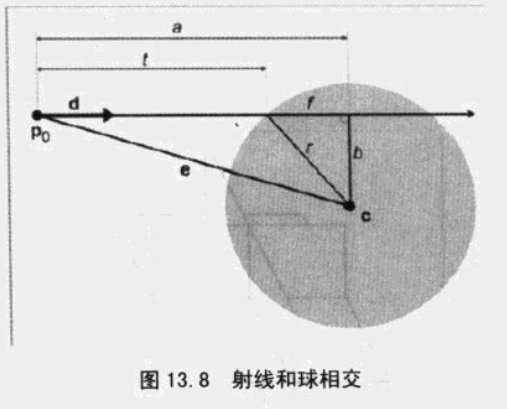
• 球的定义：圆心 $\bold{c}$ 和半径 $r$
   
• 射线的定义：$\bold{p}(t) = \bold{p}_0 + t\bold{d}$
  $\bold{d}$ 为单位向量，$t$ 从 0 变化到 $l$，$l$ 为射线长度

所要求的是交点处 $t$ 的值：$t = a - f$

• 计算 $a$ ：
  • 设 $\bold{e}$ 为从 $\bold{p_0}$ 指向 $\bold{c}$ 的向量：

  $\bold{e} = \bold{c} - \bold{p_0}$

  • 将 $\bold{e}$ 投影到 $\bold{d}$ ，这个向量的长度为 $a$ ：

  $a = \bold{e} \cdot \bold{d}$

 

• 计算 $f$ ：

$\begin{aligned} f^2 + b^2 = r^2 \\ a^2 + b^2 = e^2 \\ b^2 = e^2 - a^2 \end{aligned}$

$e$ 是从射线起点到圆心之间的距离，也就是向量 $\bold{e}$ 的长度，因此， $e^2$ 为：

$e^2 = \bold{e} \cdot \bold{e}$

代入化简得到 $f$ ：

$\begin{aligned} &f^2 + b^2 = r^2 \\ &f^2 + (e^2 - a^2) = r^2 \\ &f^2 = r^2 - e^2 + a^2 \\ &f^2 = \sqrt{r^2 - e^2 + a^2} \end{aligned}$

• 最后求得 $t$ ：

  $\begin{aligned} t &= a - f \\ &= a - \sqrt{r^2 - e^2 + a^2} \end{aligned}$

NOTE ：

• 若 $r^2 - e^2 + a^2$ 为负，则射线和圆不相交；
• 射线的起点可能在圆内，此时 $e^2 < r^2$ 。此时，根据不同的测试目的，会有不同的行为。