08 - 两个 圆_球 的相交性检测

两个 圆_球 的相交性检测

使用球心 $\bold{c_1}$ ， $\bold{c_2}$ 和半径 $r_1$ ， $r_2$ 定义的两个球，设 $d$ 为球心间的距离。

显然，当 $d < r_1 + r_2$ 时它们相交；在实现时通过比较 $d^2 < (r_1 + r_2)^2$ ，可以避免包括计算 $d$ 在内的平方根运算。

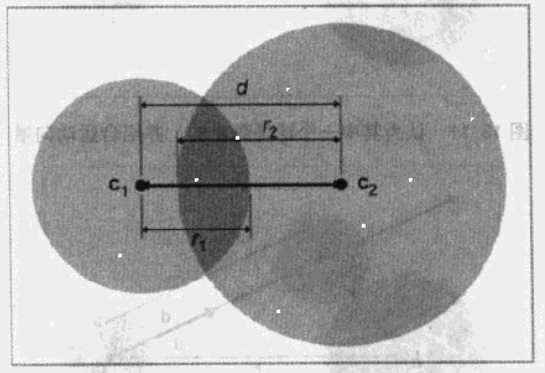
图1 两个球相交

图2 两个运动的球

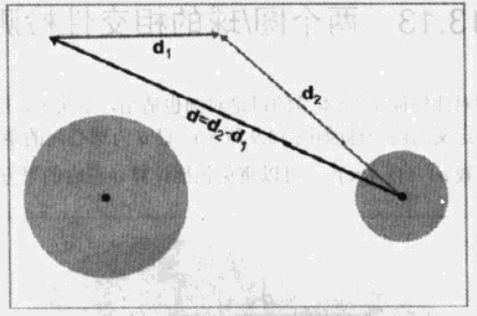
图3 认为其中一个球是静止的，并组合运动向量

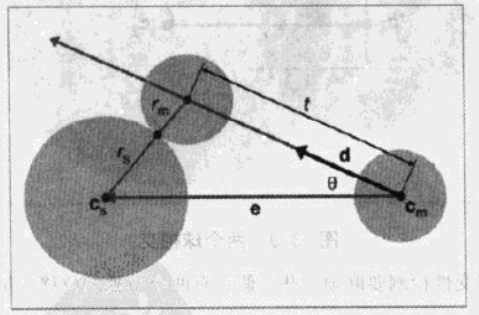
图4 球和圆的动态检测

为了计算 $t$ ，得先计算从 $\bold{c_m}$ 指向 $\bold{c_s}$ 的临时向量 $\bold{e}$ ，并设半径的和为 $r$ ：

$\begin{aligned} \bold{e} &= \bold{c_s} - \bold{c_m} \\ r &= r_m + r_s \end{aligned}$

根据 cos 定理：

$r^2 = t^2 + \Vert{\bold{e}}\Vert^2 - 2t\Vert{\bold{e}}\Vert \cos\theta$

应用点乘的集合解释，化简可得：

$\begin{aligned} r^2 &= t^2 + \Vert{\bold{e}}\Vert^2 - 2t\Vert{\bold{e}}\Vert \cos\theta \\ r^2 &= t^2 + \bold{e} \cdot \bold{e} - 2t(\bold{e} \cdot \bold{d}) \\ 0 &= t^2 - 2(\bold{e} \cdot \bold{d})t + \bold{e} \cdot \bold{e} - r^2 \end{aligned}$

应用二次求根公式：

$\begin{aligned} 0 &= t^2 - 2(\bold{e} \cdot \bold{d})t + \bold{e} \cdot \bold{e} - r^2 \\[2ex] t &= \cfrac{2(\bold{e} \cdot \bold{d}) \plusmn \sqrt{(-2(\bold{e} \cdot \bold{d}))^2 - 4(\bold{e} \cdot \bold{e} - r^2)}}{2} \\[2ex] t &= \cfrac{2(\bold{e} \cdot \bold{d}) \plusmn \sqrt{4(\bold{e} \cdot \bold{d})^2 - 4(\bold{e} \cdot \bold{e} - r^2)}}{2} \\[2ex] t &= (\bold{e} \cdot \bold{d}) \plusmn \sqrt{(\bold{e} \cdot \bold{d})^2 - \bold{e} \cdot \bold{e} + r^2)} \end{aligned}$

其中，

• 较小的值（负根）是两个球开始接触时的 $t$ 值；
• 较大的根（正根）是两个球脱离接触时的 $t$ 值。

$t = (\bold{e} \cdot \bold{d}) \plusmn \sqrt{(\bold{e} \cdot \bold{d})^2 - \bold{e} \cdot \bold{e} + r^2)}$

NOTE ：

• 若 $\Vert{\bold{e}}\Vert < r$，则球在 $t = 0$ 时就相交；
• 若 $ t < 0$ 或 $t > l$ ，那么在所讨论的时间段内两个球不会发生接触；
• 如果根号内的值是负的，那么两个球不会相交。