镜之国的爱丽丝
0%

10 - 球和平面的相交性检测

发表于 更新于 分类于 ，

1. 步骤

  • 计算球心到平面的距离 dd ；
  • 若距离 dd 小于球半径 rr 则相交。

2. 代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
// 给定一个球和平面，判断球在平面的哪一边
// 
// 如返回值；
// 
// 
// < 0 表示球完全在背面
// > 0 表示球完全在正面
// 0 表示球横跨平面

int classifySpherePlane(
                const Vector3 &planeNormal,     // 必须正则化
                float planeD,                   // p * planeNormal = planeD
                const Vector3 &sphereCenter,    // 球心
                float sphereRadius              // 球半径
            ){
    // 计算球心到平面的距离
    float d = planeNormal * sphereCenter - planeD;
    // 完全在前面？
    if(d >= sphereRadius){
        return +1;
    }
    // 完全在背面？
    if(d <= -sphereRadius){
        return -1;
    }
    // 球横跨平面
    return 0;
}

3. 动态检测

设平面为静止的，球作所有的相对位移。

平面的定义 ：p⋅n=d\bold{p} \cdot \bold{n} = d

  • n\bold{n} 为单位向量。

球的定义 ：半径 rr 和初始球心位置 c\bold{c}

球的位移 ：单位向量 d\bold{d} 指明方向， ll 代表位移的距离。tt 从 0 变化到 ll ，用直线方程 c+tdc+t\bold{d} 计算球心的运动轨迹。

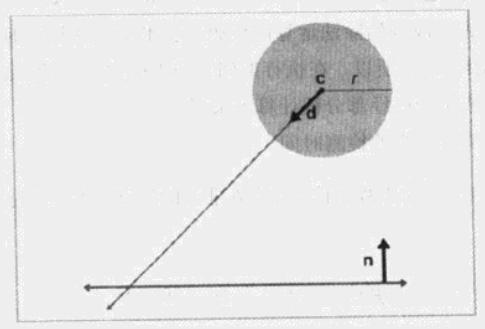
screenShot.png

图 1 球向平面移动

显然，不管在平面上的哪一点上发生相交，在球上的相交点总是固定点，用 c−rn\bold{c}-r\bold{n} 来计算交点。

screenShot.png

图 2 球和平面接触的点

在得到球上的相交点之后，使用 《04 - 射线和平面的相交性检测》 中简单的射线与平面相交性检测的方法，替换掉公式中的 p0\bold{p_0} ：

t=d−p0⋅nd⋅n=d−(c−rn)⋅nd⋅n=d−c⋅n+rd⋅n\begin{aligned} t &= \cfrac{d - \bold{p_0} \cdot \bold{n}}{\bold{d} \cdot \bold{n}} \\[2ex] &= \cfrac{d - (\bold{c}-r\bold{n}) \cdot \bold{n}}{\bold{d} \cdot \bold{n}} \\[2ex] &= \cfrac{d - \bold{c} \cdot \bold{n} + r}{\bold{d} \cdot \bold{n}} \end{aligned}