镜之国的爱丽丝
0%

07 - 欧拉角

发表于 更新于 分类于 ，

1. “ heading - pitch - bank ” 约定

欧拉角的基本思想 ：将角位移分解为绕三个互相垂直轴的三个旋转组成的序列。

先将物体坐标轴和惯性坐标轴对齐，在标准方位上，让物体依次作 heading ， pitch ， bank 旋转。

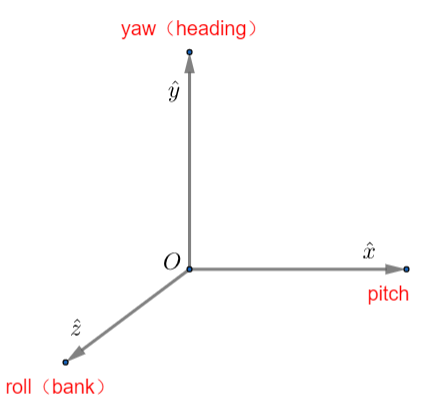
在右手坐标系下：

  • heading（航向角） ：为绕 y 轴的旋转量，面朝 +y 轴方向，逆时针为正；
  • pitch（俯仰角） ： 为绕 x 轴的旋转量，面朝 +x 轴方向，逆时针为正（注意该处是物体坐标系的 x 轴，不是惯性坐标系的 x 轴）；
  • bank（倾斜角） ： 为绕 z 轴的旋转量，面朝 +z 轴方向，逆时针为正（注意该处是物体坐标系的 z 轴，不是惯性坐标系的 z 轴）。

NOTE ：

  • 该处旋转的顺序是 “ heading - pitch - bank ” 时，是指从惯性坐标系到物体坐标系；
  • 若从物体坐标系变换到惯性坐标系，旋转的顺序就是相反的。

2. “ roll - pitch - yaw ” 约定

“ roll - pitch - yaw ” 旋转的顺序和 “ heading - pitch - bank ” 的顺序恰好相反。

roll - pitch - yaw heading - pitch - bank 含 义
roll （翻滚角） bank （倾斜角） 绕 z 轴的旋转量
pitch （俯仰角） pitch （俯仰角） 绕 x 轴的旋转量
yaw （偏航角） heading （航向角） 绕 y 轴的旋转量

screenShot.png

3. 限制范围

限定一个范围，使得对于任意方位，仅存在一个限制欧拉角能代表这个方位。

heading - pitch - bank 含 义 取值范围
heading （航向角） 绕 y 轴的旋转量 [−180°,180°][-180° , 180°]
pitch （俯仰角） 绕 x 轴的旋转量 [−90°,90°][-90° , 90°]
bank （倾斜角） 绕 z 轴的旋转量 [−180°,180°][-180° , 180°]

4. 万向锁

eg ：先 heading=45°heading = 45° 再 pitch=90°pitch = 90° ，这与先 pitch=90°pitch = 90° 再 bank=45°bank = 45° 是等价的。

  • 事实上一旦选择 pitch=±90°pitch = \plusmn 90° ，物体就被限制在只能绕竖直轴旋转。

4.1 万向锁现象 ：

角度为 ±90°\plusmn 90° 的第二次旋转使得第一次和第三次旋转的旋转轴相同。

4.2 消除万向锁 ：

  • 规定万向锁情况下由 headingheading 完成绕竖直轴的全部旋转；
  • 换言之，在限制欧拉角中，若 pitch=±90°pitch = \plusmn 90° ，则 bankbank 锁定为零。

5. 欧拉角的插值运算

在方位 A 和 B 间求插值 ：

给定参数 t∈[0,1]t \in [0 , 1] ，计算临时方位 C ，当 tt 从 00 变化到 11 时，C 也平滑地从 A 变化到 B。

该问题的简单解法是分别对三个角度作 标准线性插值 ：

{Δθ=θ1−θ0θt=θ0+tΔθ\begin{cases} \Delta \theta = \theta_{1} - \theta_{0} \\[1.5ex] \theta_{t} = \theta_{0} + t\Delta \theta \end{cases}

然而以这种方式，即便是限制欧拉角也无法解决某个问题，该问题是由旋转角度的周期性引起的。

例如，A−heading=−170°A - heading = -170° ，B−heading=170°B - heading = 170° ，这些值都在 headingheading 的限制范围内，都在 −180°-180° 到 +180°+180° 之间。

然而这两个值只相差 20°20° ，这时插值操作发生了错误，因为旋转是沿着“长弧”饶了 340°340° 而不是更短的 20°20° 。

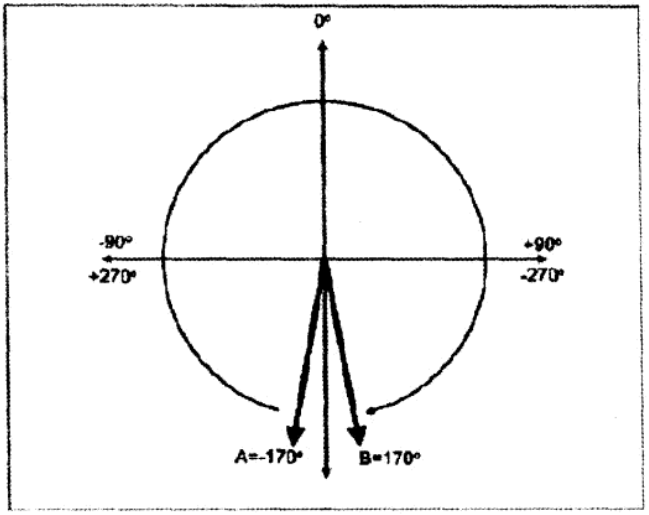
screenShot.png

解决方式 ：

解决这类问题的方法是将插值的 “ 差 ” 角度折到 −180°-180° 到 +180°+180° 之间，以找到最短弧。

wrap(x)=x−360°⋅⌊(x+180°)/360°⌋wrap(x) = x - 360° \cdot \lfloor {(x + 180°) / 360°} \rfloor

kk 取值范围 xx 取值范围 含 义
k∈Z,k∈[0,+∞)k \in Z , k \in [0 , +\infty) x∈[2kπ,π+2kπ)x \in [2k \pi , \pi + 2k \pi ) x=xmod  2πx = x \mod{2 \pi}
k∈Z,k∈[0,+∞)k \in Z , k \in [0 , +\infty) x∈[π+2kπ,2π+2kπ)x \in [\pi + 2k \pi , 2 \pi + 2k \pi ) x=(xmod  2π)−2πx = (x \mod{2 \pi}) - 2 \pi
k∈Z,k∈(−∞,0]k \in Z , k \in (-\infty , 0] x∈[2kπ−π,2kπ)x \in [2k \pi - \pi , 2k \pi ) x=xmod  2πx = x \mod{2 \pi}
k∈Z,k∈(−∞,0]k \in Z , k \in (-\infty , 0] x∈[2kπ−2π,2kπ−π)x \in [2k \pi - 2 \pi , 2k \pi - \pi ) x=(xmod  2π)+2πx = (x \mod{2 \pi}) + 2 \pi

screenShot.png

1
2
3
4
5
6
7
8
9
//---------------------------------------------------------------------------
// 通过加上适当的 2pi 倍数，将角度限制在 -pi 到 pi 的区间内

float wrapPi(float theta) {
	theta += kPi;
	theta -= floor(theta * k1Over2Pi) * k2Pi;
	theta -= kPi;
	return theta;
}

即将 标准线性插值 改进如下：

{Δθ=wrap(θ1−θ0)θt=θ0+tΔθ\begin{cases} \Delta \theta = wrap(\theta_{1} - \theta_{0}) \\[1.5ex] \theta_{t} = \theta_{0} + t\Delta \theta \end{cases}

6. 示例代码

6.1 将欧拉角转换到限制集

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
//---------------------------------------------------------------------------
// EulerAngles::canonize
//
// 将欧拉角转换到限制集中
// 就表示 3D 方位的目的而言，它不会改变欧拉角的值
// 但对于其他表示对象如角速度等，则会产生影响

void EulerAngles::canonize() {

	// 首先，将 pitch 变换到 -pi 到 pi 之间
	pitch = wrapPi(pitch);

	// 现在将 pitch 变换到 -pi/2 到 pi/2 之间
	if (pitch < -kPiOver2) {
		pitch = -kPi - pitch;
		heading += kPi;
		bank += kPi;
	}
	else if (pitch > kPiOver2) {
		pitch = kPi - pitch;
		heading += kPi;
		bank += kPi;
	}

	// 现在检查万向锁的情况，允许存在一定的误差
	if (fabs(pitch) > kPiOver2 - 1e-4) {

		// 在万向锁中，将所有绕垂直轴的旋转赋给 heading
		heading += bank;
		bank = 0.0f;

	}
	else {

		// 非万向锁，将 bank 转换到限制集中
		bank = wrapPi(bank);
	}

	// 将 heading 转换到限制集中
	heading = wrapPi(heading);
}

6.1.1 将 pitch 变换到 −π2-\cfrac{\pi}{2} 到 π2\cfrac{\pi}{2} 之间

<1> pitch<−π2pitch < -\cfrac{\pi}{2} :

{pitch=−π−pitchheading=heading+πbank=bank+π\begin{cases} pitch = - \pi - pitch \\[1.5ex] heading = heading + \pi \\[1.5ex] bank = bank + \pi \end{cases}

  • 计算 pitchpitch :

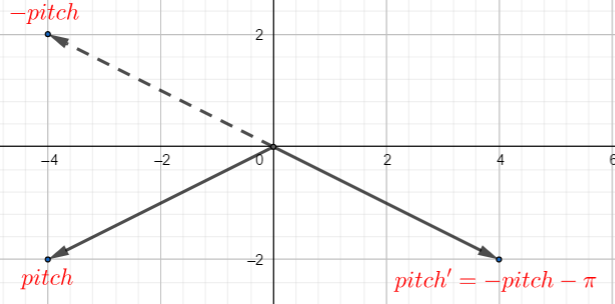
screenShot.png

  • 将 headingheading 与 bankbank 反向

<2> pitch>π2pitch > \cfrac{\pi}{2} :

{pitch=π−pitchheading=heading+πbank=bank+π\begin{cases} pitch = \pi - pitch \\[1.5ex] heading = heading + \pi \\[1.5ex] bank = bank + \pi \end{cases}

  • 计算 pitchpitch :

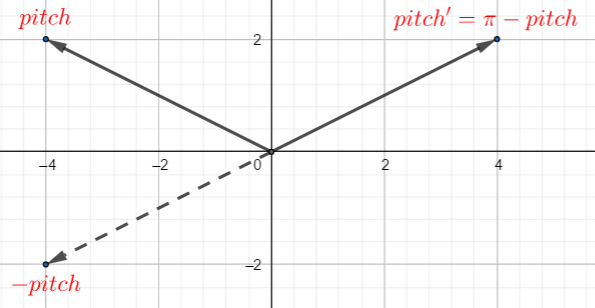
screenShot.png

  • 将 headingheading 与 bankbank 反向

6.1.2 处理万向锁

pitch=±90°:{heading=heading+bankbank=0pitch = \plusmn 90° : \begin{cases} heading = heading + bank \\[1.5ex] bank = 0 \end{cases}