一个四元数包含一个 标量分量(实部) 和一个 3D 向量分量(虚部) 。
经常记标量分量为 w w w v = ( x , y , z ) \bold{v} = (x, y, z) v = ( x , y , z )
{ [ w , v ] [ w , ( x , y , z ) ] \begin{cases}
[w, \bold{v}] \\[1.5ex]
[w, (x, y, z)]
\end{cases}
⎩ ⎨ ⎧ [ w , v ] [ w , ( x , y , z ) ]
复数 对一个二维坐标 ( a , b ) (a, b) ( a , b ) a + b i a + bi a + b i i i i 虚数 ,其中:
i 2 = − 1 i^2 = -1 i 2 = − 1 a a a b b b
NOTE :
实数集 自身也包含于 复数集 中,任何实数 k k k ( k , 0 ) = k + 0 ⋅ i (k, 0) = k + 0 \cdot i ( k , 0 ) = k + 0 ⋅ i
复数能够相加、相减、相乘
( a + b i ) + ( c + d i ) = ( a + c ) + ( b + d ) i ( a + b i ) − ( c + d i ) = ( a − c ) + ( b − d ) i ( a + b i ) ⋅ ( c + d i ) = a c + a d ⋅ i + b c ⋅ i + b d ⋅ i 2 = ( a c − b d ) + ( a d + b c ) ⋅ i \begin{aligned}
(a + bi) + (c + di) &= (a + c) + (b + d)i \\[2ex]
(a + bi) - (c + di) &= (a - c) + (b - d)i \\[2ex]
(a + bi) \cdot (c + di) &= ac + ad \cdot i + bc \cdot i + bd \cdot i^2 \\
&= (ac - bd) + (ad + bc) \cdot i
\end{aligned}
( a + b i ) + ( c + d i ) ( a + b i ) − ( c + d i ) ( a + b i ) ⋅ ( c + d i ) = ( a + c ) + ( b + d ) i = ( a − c ) + ( b − d ) i = a c + a d ⋅ i + b c ⋅ i + b d ⋅ i 2 = ( a c − b d ) + ( a d + b c ) ⋅ i
通过使虚部变负,获得复数的 共轭
{ p = ( a + b i ) p ∗ = ( a − b i ) \begin{cases}
\bold{p} = (a + bi) \\[1.5ex]
\bold{p^*} = (a - bi)
\end{cases}
⎩ ⎨ ⎧ p = ( a + b i ) p ∗ = ( a − b i )
∥ p ∥ = p ⋅ p ∗ ∥ a + b i ∥ = ( a + b i ) ( a + b i ) ∗ = ( a + b i ) ( a − b i ) = a 2 + b 2 \begin{aligned}
\Vert {\bold{p}} \Vert &= \sqrt{\bold{p} \cdot \bold{p^*}} \\[2ex]
\Vert {a + bi} \Vert &= \sqrt{(a + bi)(a + bi)^*} \\
&= \sqrt{(a + bi)(a - bi)} \\
&= \sqrt{a^2 + b^2}
\end{aligned}
∥ p ∥ ∥ a + b i ∥ = p ⋅ p ∗ = ( a + b i ) ( a + b i ) ∗ = ( a + b i ) ( a − b i ) = a 2 + b 2
关于如何用复数来表示二维空间的线性变换,见 《01 - 线性变换》 4 使用复数表示线性变换:
复数存在于一个 2D 平面上,可认为这个平面有两个轴:实轴 和 虚轴 ;
就能将复数 ( x , y ) (x, y) ( x , y )
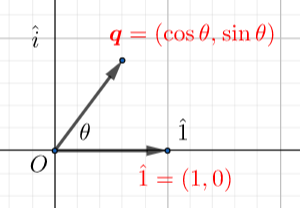
复数 p \bold{p} p θ \theta θ
p = a + b ⋅ i q = cos θ + sin θ ⋅ i p ′ = p ⋅ q = ( a + b ⋅ i ) ⋅ ( cos θ + sin θ ⋅ i ) = ( a cos θ − b sin θ ) + ( a sin θ + b cos θ ) ⋅ i \begin{aligned}
\bold{p} &= a + b \cdot i \\[2ex]
\bold{q} &= \cos{\theta} + \sin{\theta} \cdot i \\[2ex]
\bold{p'} &= \bold{p} \cdot \bold{q} \\[1.25ex]
&= (a + b \cdot i) \cdot (\cos{\theta} + \sin{\theta} \cdot i) \\[1.25ex]
&= (a\cos{\theta} - b\sin{\theta}) + (a\sin{\theta} + b\cos{\theta}) \cdot i
\end{aligned}
p q p ′ = a + b ⋅ i = cos θ + sin θ ⋅ i = p ⋅ q = ( a + b ⋅ i ) ⋅ ( cos θ + sin θ ⋅ i ) = ( a cos θ − b sin θ ) + ( a sin θ + b cos θ ) ⋅ i
四元数 是 复数 的一种扩展,如果说复数可以描述 2D 空间中的变换,那么四元数就是描述 3D 空间中的变换。
{ i 2 = j 2 = k 2 = − 1 i j = k , j i = − k j k = i , k j = − i k i = j , i k = − j \begin{cases}
i^2 = j^2 = k^2 = - 1 \\[1.5ex]
ij = k \space,\space ji = - k \\[1.5ex]
jk = i \space,\space kj = - i \\[1.5ex]
ki = j \space,\space ik = - j
\end{cases}
⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ i 2 = j 2 = k 2 = − 1 i j = k , j i = − k j k = i , k j = − i k i = j , i k = − j
各个不同的虚部相乘的结果类似于向量的 叉乘 ,方向可依此确定;
一个四元数 [ w , ( x , y , z ) ] [w, (x, y, z)] [ w , ( x , y , z ) ] ( w + x i + y j + z k ) (w + xi + yj + zk) ( w + x i + y j + z k )
欧拉证明了一个旋转序列等价于单个旋转:
符 号
n \bold{n} n 旋转轴
由于仅表示方向,因此长度无意义,不妨设置其为单位向量
θ \theta θ 绕轴旋转的量
根据 “右手法则” 定义旋转的 “正” 方向
因此可以通过一个 “ 轴 - 角对 ” ( n , θ ) (\bold{n}, \theta) ( n , θ ) 角位移 :绕 n \bold{n} n θ \theta θ
四元数能被解释为角位移的 “ 轴 - 角对 ” 表示方式
然而, n \bold{n} n θ \theta θ
q = [ cos ( θ 2 ) sin ( θ 2 ) ⋅ n ] = [ cos ( θ 2 ) sin ( θ 2 ) ⋅ n x sin ( θ 2 ) ⋅ n y sin ( θ 2 ) ⋅ n z ] \begin{aligned}
\bold{q} &=
\begin{bmatrix}
\cos{(\space \cfrac{\theta}{2} \space)} & \sin{(\space \cfrac{\theta}{2} \space)} \cdot \bold{n}
\end{bmatrix} \\[2ex]
&=
\begin{bmatrix}
\cos{(\space \cfrac{\theta}{2} \space)} & \sin{(\space \cfrac{\theta}{2} \space)} \cdot \bold{n}_x & \sin{(\space \cfrac{\theta}{2} \space)} \cdot \bold{n}_y & \sin{(\space \cfrac{\theta}{2} \space)} \cdot \bold{n}_z
\end{bmatrix}
\end{aligned}
q = [ cos ( 2 θ ) sin ( 2 θ ) ⋅ n ] = [ cos ( 2 θ ) sin ( 2 θ ) ⋅ n x sin ( 2 θ ) ⋅ n y sin ( 2 θ ) ⋅ n z ]
NOTE :
q \bold{q} q w \bold{w} w θ \theta θ 向量 v \bold{v} v n \bold{n} n
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 void Quaternion::setToRotateAboutX (float theta) float thetaOver2 = theta * .5 f; w = cos (thetaOver2); x = sin (thetaOver2); y = 0.0f ; z = 0.0f ; } void Quaternion::setToRotateAboutY (float theta) float thetaOver2 = theta * .5 f; w = cos (thetaOver2); x = 0.0f ; y = sin (thetaOver2); z = 0.0f ; } void Quaternion::setToRotateAboutZ (float theta) float thetaOver2 = theta * .5 f; w = cos (thetaOver2); x = 0.0f ; y = 0.0f ; z = sin (thetaOver2); } void Quaternion::setToRotateAboutAxis (const Vector3& axis, float theta) assert(fabs (vectorMag(axis) - 1.0f ) < .01 f); float thetaOver2 = theta * .5 f; float sinThetaOver2 = sin (thetaOver2); w = cos (thetaOver2); x = axis.x * sinThetaOver2; y = axis.y * sinThetaOver2; z = axis.z * sinThetaOver2; } float Quaternion::getRotationAngle () const float thetaOver2 = safeAcos(w); return thetaOver2 * 2.0f ; } Vector3 Quaternion::getRotationAxis () const { float sinThetaOver2Sq = 1.0f - w * w; if (sinThetaOver2Sq <= 0.0f ) { return Vector3(1.0f , 0.0f , 0.0f ); } float oneOverSinThetaOver2 = 1.0f / sqrt (sinThetaOver2Sq); return Vector3( x * oneOverSinThetaOver2, y * oneOverSinThetaOver2, z * oneOverSinThetaOver2 ); }
四元数求负,将每个分量都取负。
− q = [ w ( x y z ) ] = [ − w ( − x − y − z ) ] = [ w v ] = [ − w − v ] \begin{aligned}
-\bold{q} &= \begin{bmatrix} w &(x &y &z) \end{bmatrix}
= \begin{bmatrix} -w &(-x &-y &-z) \end{bmatrix} \\[2ex]
&= \begin{bmatrix} w &\bold{v} \end{bmatrix}
= \begin{bmatrix} -w &-\bold{v} \end{bmatrix}
\end{aligned}
− q = [ w ( x y z ) ] = [ − w ( − x − y − z ) ] = [ w v ] = [ − w − v ]
q \bold{q} q − q \bold{-q} − q θ \theta θ 360 ° 360° 3 6 0 ° q \bold{q} q q \bold{q} q
因此,3D 中的任意角位移都有两种不同的四元数表示方法,他们互相为负。
几何上,存在两个 单位元 ,他们代表没有角位移:[ 1 , 0 ] [1,\space \bold{0}] [ 1 , 0 ] [ − 1 , 0 ] [-1,\space \bold{0}] [ − 1 , 0 ] 0 \bold{0} 0
θ \theta θ 形 式
θ = 2 k ⋅ 2 π \theta = 2k \cdot 2\pi θ = 2 k ⋅ 2 π θ \theta θ 360 ° 360° 3 6 0 ° cos ( θ / 2 ) = 1 \cos{(\theta/2)} = 1 cos ( θ / 2 ) = 1
θ = ( 2 k + 1 ) ⋅ 2 π \theta = (2k + 1) \cdot 2\pi θ = ( 2 k + 1 ) ⋅ 2 π θ \theta θ 360 ° 360° 3 6 0 ° cos ( θ / 2 ) = − 1 \cos{(\theta/2)} = -1 cos ( θ / 2 ) = − 1
显然,上述两种情况下,都有 sin ( θ / 2 ) = 0 \sin{(\theta/2)} = 0 sin ( θ / 2 ) = 0 n \bold{n} n
当旋转角 θ \theta θ 360 ° 360° 3 6 0 ° n \bold{n} n
数学上,实际只定义一个单位元四元数:[ 1 , 0 ] [1,\space \bold{0}] [ 1 , 0 ]
{ q ⋅ [ 1 , 0 ] = q q ⋅ [ − 1 , 0 ] = − q \begin{cases}
\bold{q} \cdot [1,\space \bold{0}] = \bold{q} \\[2ex]
\bold{q} \cdot [-1,\space \bold{0}] = \bold{-q}
\end{cases}
⎩ ⎨ ⎧ q ⋅ [ 1 , 0 ] = q q ⋅ [ − 1 , 0 ] = − q
几何意义 :q \bold{q} q − q \bold{-q} − q 数学意义 :q \bold{q} q − q \bold{-q} − q [ − 1 , 0 ] [-1,\space \bold{0}] [ − 1 , 0 ]
1 2 3 4 5 const Quaternion kQuaternionIdentity = { 1.0f , 0.0f , 0.0f , 0.0f };
∥ q ∥ = ∥ [ w ( x y z ) ] ∥ = w 2 + x 2 + y 2 + z 2 = ∥ [ w v ] ∥ = w 2 + ∥ v ∥ 2 \begin{aligned}
\Vert {\bold{q}} \Vert &= \left \Vert {\begin{bmatrix} w &(x &y &z) \end{bmatrix}} \right \Vert
= \sqrt{w^2 + x^2 + y^2 + z^2} \\[2ex]
&= \left \Vert {\begin{bmatrix} w &\bold{v} \end{bmatrix}} \right \Vert
= \sqrt{w^2 + \Vert {\bold{v}} \Vert^2}
\end{aligned}
∥ q ∥ = ∥ ∥ [ w ( x y z ) ] ∥ ∥ = w 2 + x 2 + y 2 + z 2 = ∥ ∥ [ w v ] ∥ ∥ = w 2 + ∥ v ∥ 2
几何意义 :代入 θ \theta θ n \bold{n} n
∥ q ∥ = ∥ [ w v ] ∥ = w 2 + ∥ v ∥ 2 = cos 2 ( θ / 2 ) + ( sin ( θ / 2 ) ∥ n ∥ ) 2 = cos 2 ( θ / 2 ) + sin 2 ( θ / 2 ) ∥ n ∥ 2 = cos 2 ( θ / 2 ) + sin 2 ( θ / 2 ) ( 1 ) = cos 2 ( θ / 2 ) + sin 2 ( θ / 2 ) = 1 = 1 \begin{aligned}
\Vert {\bold{q}} \Vert &= \left \Vert {\begin{bmatrix} w &\bold{v} \end{bmatrix}} \right \Vert \\[1.5ex]
&= \sqrt{w^2 + \Vert {\bold{v}} \Vert^2} \\[1.5ex]
&= \sqrt{\cos^2(\theta/2) + (\sin(\theta/2)\Vert{\bold{n}}\Vert)^2} \\[1.5ex]
&= \sqrt{\cos^2(\theta/2) + \sin^2(\theta/2)\Vert{\bold{n}}\Vert^2} \\[1.5ex]
&= \sqrt{\cos^2(\theta/2) + \sin^2(\theta/2)(1)} \\[1.5ex]
&= \sqrt{\cos^2(\theta/2) + \sin^2(\theta/2)} = \sqrt{1} = 1
\end{aligned}
∥ q ∥ = ∥ ∥ [ w v ] ∥ ∥ = w 2 + ∥ v ∥ 2 = cos 2 ( θ / 2 ) + ( sin ( θ / 2 ) ∥ n ∥ ) 2 = cos 2 ( θ / 2 ) + sin 2 ( θ / 2 ) ∥ n ∥ 2 = cos 2 ( θ / 2 ) + sin 2 ( θ / 2 ) ( 1 ) = cos 2 ( θ / 2 ) + sin 2 ( θ / 2 ) = 1 = 1
若用四元数来表示方位,仅适用符合该规则的 单位四元数 。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 void Quaternion::normalize () float mag = (float )sqrt (w * w + x * x + y * y + z * z); if (mag > 0.0f ) { float oneOverMag = 1.0f / mag; w *= oneOverMag; x *= oneOverMag; y *= oneOverMag; z *= oneOverMag; } else { assert(false ); identity(); } }
四元数的共轭 记作 q ∗ \bold{q}^* q ∗
q ∗ = [ w v ] ∗ = [ w − v ] = [ w ( x y z ) ] ∗ = [ w ( − x − y − z ) ] \begin{aligned}
\bold{q}^* &= \begin{bmatrix} w &\bold{v} \end{bmatrix}^* = \begin{bmatrix} w &-\bold{v} \end{bmatrix} \\[1.5ex]
&= \begin{bmatrix} w &(x &y &z) \end{bmatrix}^* = \begin{bmatrix} w &(-x &-y &-z) \end{bmatrix}
\end{aligned}
q ∗ = [ w v ] ∗ = [ w − v ] = [ w ( x y z ) ] ∗ = [ w ( − x − y − z ) ]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 Quaternion conjugate (const Quaternion& q) { Quaternion result; result.w = q.w; result.x = -q.x; result.y = -q.y; result.z = -q.z; return result; }
四元数的逆 记作 q − 1 \bold{q^{-1}} q − 1
q − 1 = q ∗ ∥ q ∥ \bold{q^{-1}} = \cfrac{\bold{q^*}}{\Vert{\bold{q}}\Vert}
q − 1 = ∥ q ∥ q ∗
其中有:
q q − 1 = [ 1 , 0 ] \bold{q} \bold{q^{-1}} = [1,\space \bold{0}]
q q − 1 = [ 1 , 0 ]
若 q \bold{q} q ∥ q ∥ = 1 \Vert {\bold{q}} \Vert = 1 ∥ q ∥ = 1
q − 1 = q ∗ \bold{q^{-1}} = \bold{q^*}
q − 1 = q ∗
共轭的几何意义 :q \bold{q} q q ∗ \bold{q^*} q ∗
当 v \bold{v} v q \bold{q} q θ \theta θ q ∗ \bold{q^*} q ∗
另一种几何意义 :q \bold{q} q q − 1 \bold{q^{-1}} q − 1
类似于复数的乘法:
q 1 × q 2 = ( w 1 + x 1 i ^ + y 1 j ^ + z 1 k ^ ) ( w 2 + x 2 i ^ + y 2 j ^ + z 2 k ^ ) = w 1 w 2 + w 1 x 2 i ^ + w 1 y 2 j ^ + w 1 z 2 k ^ + x 1 w 2 i ^ + x 1 x 2 i ^ 2 + x 1 y 2 i ^ j ^ + x 1 z 2 i ^ k ^ + y 1 w 2 j ^ + y 1 x 2 j ^ i ^ + y 1 y 2 j ^ 2 + y 1 z 2 j ^ k ^ + z 1 w 2 k ^ + z 1 x 2 k ^ i ^ + z 1 y 2 k ^ j ^ + z 1 z 2 k ^ 2 = w 1 w 2 + w 1 x 2 i ^ + w 1 y 2 j ^ + w 1 z 2 k ^ + x 1 w 2 i ^ + x 1 x 2 ( − 1 ) + x 1 y 2 ( k ^ ) + x 1 z 2 ( − j ^ ) + y 1 w 2 j ^ + y 1 x 2 ( − k ^ ) + y 1 y 2 ( − 1 ) + y 1 z 2 ( i ^ ) + z 1 w 2 k ^ + z 1 x 2 ( j ^ ) + z 1 y 2 ( − i ^ ) + z 1 z 2 ( − 1 ) = w 1 w 2 − x 1 x 2 − y 1 y 2 − z 1 z 2 + ( w 1 x 2 + x 1 w 2 + y 1 z 2 − z 1 y 2 ) i ^ + ( w 1 y 2 + y 1 w 2 + z 1 x 2 − x 1 z 2 ) j ^ + ( w 1 z 2 + z 1 w 2 + x 1 y 2 − y 1 x 2 ) k ^ \begin{aligned}
\bold{q_1} \times \bold{q_2} & = && (w_1 + x_1\hat{i} + y_1\hat{j} + z_1\hat{k})(w_2 + x_2\hat{i} + y_2\hat{j} + z_2\hat{k}) \\[1.5ex]
& = && w_1w_2 + w_1x_2\hat{i} + w_1y_2\hat{j} + w_1z_2\hat{k} \\
& && + x_1w_2\hat{i} + x_1x_2\hat{i}^2 + x_1y_2\hat{i}\hat{j} + x_1z_2\hat{i}\hat{k} \\
& && + y_1w_2\hat{j} + y_1x_2\hat{j}\hat{i} + y_1y_2\hat{j}^2 + y_1z_2\hat{j}\hat{k} \\
& && + z_1w_2\hat{k} + z_1x_2\hat{k}\hat{i} + z_1y_2\hat{k}\hat{j} + z_1z_2\hat{k}^2 \\[1.5ex]
& = && w_1w_2 + w_1x_2\hat{i} + w_1y_2\hat{j} + w_1z_2\hat{k} \\
& && + x_1w_2\hat{i} + x_1x_2(-1) + x_1y_2(\hat{k}) + x_1z_2(-\hat{j}) \\
& && + y_1w_2\hat{j} + y_1x_2(-\hat{k}) + y_1y_2(-1) + y_1z_2(\hat{i}) \\
& && + z_1w_2\hat{k} + z_1x_2(\hat{j}) + z_1y_2(-\hat{i}) + z_1z_2(-1) \\[1.5ex]
& = && w_1w_2 - x_1x_2 - y_1y_2 - z_1z_2 \\
& && + (w_1x_2 + x_1w_2 + y_1z_2 - z_1y_2)\hat{i} \\
& && + (w_1y_2 + y_1w_2 + z_1x_2 - x_1z_2)\hat{j} \\
& && + (w_1z_2 + z_1w_2 + x_1y_2 - y_1x_2)\hat{k}
\end{aligned}
q 1 × q 2 = = = = ( w 1 + x 1 i ^ + y 1 j ^ + z 1 k ^ ) ( w 2 + x 2 i ^ + y 2 j ^ + z 2 k ^ ) w 1 w 2 + w 1 x 2 i ^ + w 1 y 2 j ^ + w 1 z 2 k ^ + x 1 w 2 i ^ + x 1 x 2 i ^ 2 + x 1 y 2 i ^ j ^ + x 1 z 2 i ^ k ^ + y 1 w 2 j ^ + y 1 x 2 j ^ i ^ + y 1 y 2 j ^ 2 + y 1 z 2 j ^ k ^ + z 1 w 2 k ^ + z 1 x 2 k ^ i ^ + z 1 y 2 k ^ j ^ + z 1 z 2 k ^ 2 w 1 w 2 + w 1 x 2 i ^ + w 1 y 2 j ^ + w 1 z 2 k ^ + x 1 w 2 i ^ + x 1 x 2 ( − 1 ) + x 1 y 2 ( k ^ ) + x 1 z 2 ( − j ^ ) + y 1 w 2 j ^ + y 1 x 2 ( − k ^ ) + y 1 y 2 ( − 1 ) + y 1 z 2 ( i ^ ) + z 1 w 2 k ^ + z 1 x 2 ( j ^ ) + z 1 y 2 ( − i ^ ) + z 1 z 2 ( − 1 ) w 1 w 2 − x 1 x 2 − y 1 y 2 − z 1 z 2 + ( w 1 x 2 + x 1 w 2 + y 1 z 2 − z 1 y 2 ) i ^ + ( w 1 y 2 + y 1 w 2 + z 1 x 2 − x 1 z 2 ) j ^ + ( w 1 z 2 + z 1 w 2 + x 1 y 2 − y 1 x 2 ) k ^
四元数乘法的标准定义,以下是两种四元数记法:
[ w 1 ( x 1 y 1 z 1 ) ] × [ w 2 ( x 2 y 2 z 2 ) ] = [ w 1 w 2 − x 1 x 2 − y 1 y 2 − z 1 z 2 w 1 x 2 + x 1 w 2 + y 1 z 2 − z 1 y 2 w 1 y 2 + y 1 w 2 + z 1 x 2 − x 1 z 2 w 1 z 2 + z 1 w 2 + x 1 y 2 − y 1 x 2 ] \begin{aligned}
& \begin{bmatrix} w_1 &(x_1 &y_1 &z_1) \end{bmatrix} \times \begin{bmatrix} w_2 &(x_2 &y_2 &z_2) \end{bmatrix} \\[2ex]
& =
\begin{bmatrix}
w_1w_2 - x_1x_2 - y_1y_2 - z_1z_2 \\[1.25ex] \hdashline
w_1x_2 + x_1w_2 + y_1z_2 - z_1y_2 \\[1.25ex]
w_1y_2 + y_1w_2 + z_1x_2 - x_1z_2 \\[1.25ex]
w_1z_2 + z_1w_2 + x_1y_2 - y_1x_2
\end{bmatrix}
\end{aligned}
[ w 1 ( x 1 y 1 z 1 ) ] × [ w 2 ( x 2 y 2 z 2 ) ] = ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ w 1 w 2 − x 1 x 2 − y 1 y 2 − z 1 z 2 w 1 x 2 + x 1 w 2 + y 1 z 2 − z 1 y 2 w 1 y 2 + y 1 w 2 + z 1 x 2 − x 1 z 2 w 1 z 2 + z 1 w 2 + x 1 y 2 − y 1 x 2 ⎦ ⎥ ⎥ ⎥ ⎥ ⎤
[ w 1 v 1 ] × [ w 2 v 2 ] = [ w 1 w 2 − v 1 ⋅ v 2 w 1 v 2 + w 2 v 1 + v 2 × v 1 ] \begin{aligned}
& \begin{bmatrix} w_1 &\bold{v_1} \end{bmatrix} \times \begin{bmatrix} w_2 &\bold{v_2} \end{bmatrix} \\[2ex]
& = \begin{bmatrix}
w_1w_2 - \bold{v_1} \cdot \bold{v_2}
&w_1\bold{v_2} + w_2\bold{v_1} + \bold{v_2} \times \bold{v_1}
\end{bmatrix}
\end{aligned}
[ w 1 v 1 ] × [ w 2 v 2 ] = [ w 1 w 2 − v 1 ⋅ v 2 w 1 v 2 + w 2 v 1 + v 2 × v 1 ]
四元数乘法满足结合律不满足交换律:
{ ( a × b ) × c = a × ( b × c ) a × b ≠ b × a \begin{cases}
(\bold{a} \times \bold{b}) \times \bold{c} = \bold{a} \times (\bold{b} \times \bold{c}) \\[2ex]
\bold{a} \times \bold{b} \ne \bold{b} \times \bold{a}
\end{cases}
⎩ ⎨ ⎧ ( a × b ) × c = a × ( b × c ) a × b = b × a
两四元数叉乘的模:
∥ q 1 × q 2 ∥ = ∥ [ w 1 ( x 1 y 1 z 1 ) ] × [ w 2 ( x 2 y 2 z 2 ) ] ∥ = ∥ [ w 1 w 2 − x 1 x 2 − y 1 y 2 − z 1 z 2 w 1 x 2 + x 1 w 2 + y 1 z 2 − z 1 y 2 w 1 y 2 + y 1 w 2 + z 1 x 2 − x 1 z 2 w 1 z 2 + z 1 w 2 + x 1 y 2 − y 1 x 2 ] ∥ = ( w 1 w 2 − x 1 x 2 − y 1 y 2 − z 1 z 2 ) 2 + ( w 1 x 2 + x 1 w 2 + y 1 z 2 − z 1 y 2 ) 2 + ( w 1 y 2 + y 1 w 2 + z 1 x 2 − x 1 z 2 ) 2 + ( w 1 z 2 + z 1 w 2 + x 1 y 2 − y 1 x 2 ) 2 = w 1 2 w 2 2 + x 1 2 x 2 2 + y 1 2 y 2 2 + z 1 2 z 2 2 + w 1 2 x 2 2 + x 1 2 w 2 2 + y 1 2 z 2 2 + z 1 2 y 2 2 + w 1 2 y 2 2 + y 1 2 w 2 2 + z 1 2 x 2 2 + x 1 2 z 2 2 + w 1 2 z 2 2 + z 1 2 w 2 2 + x 1 2 y 2 2 + y 1 2 x 2 2 = w 1 2 ( w 2 2 + x 2 2 + y 2 2 + z 2 2 ) + x 1 2 ( w 2 2 + x 2 2 + y 2 2 + z 2 2 ) + y 1 2 ( w 2 2 + x 2 2 + y 2 2 + z 2 2 ) + z 1 2 ( w 2 2 + x 2 2 + y 2 2 + z 2 2 ) = ( w 1 2 + x 1 2 + y 1 2 + z 1 2 ) ( w 2 2 + x 2 2 + y 2 2 + z 2 2 ) \begin{aligned}
\Vert {\bold{q_1} \times \bold{q_2}} \Vert & = \left \Vert {\begin{bmatrix} w_1 &(x_1 &y_1 &z_1) \end{bmatrix} \times \begin{bmatrix} w_2 &(x_2 &y_2 &z_2) \end{bmatrix}} \right \Vert \\[2ex]
& =
\left \Vert
\begin{bmatrix}
w_1w_2 - x_1x_2 - y_1y_2 - z_1z_2 \\[1.25ex] \hdashline
w_1x_2 + x_1w_2 + y_1z_2 - z_1y_2 \\[1.25ex]
w_1y_2 + y_1w_2 + z_1x_2 - x_1z_2 \\[1.25ex]
w_1z_2 + z_1w_2 + x_1y_2 - y_1x_2
\end{bmatrix}
\right \Vert \\[2ex]
& = \sqrt{
\begin{aligned}
(w_1w_2 - x_1x_2 - y_1y_2 - z_1z_2)^2 \\
+(w_1x_2 + x_1w_2 + y_1z_2 - z_1y_2)^2 \\
+(w_1y_2 + y_1w_2 + z_1x_2 - x_1z_2)^2 \\
+(w_1z_2 + z_1w_2 + x_1y_2 - y_1x_2)^2
\end{aligned}
} \\[2ex]
& = \sqrt{
\begin{aligned}
w_1^2 w_2^2 + x_1^2 x_2^2 + y_1^2 y_2^2 + z_1^2 z_2^2 \\
+w_1^2 x_2^2 + x_1^2 w_2^2 + y_1^2 z_2^2 + z_1^2 y_2^2 \\
+w_1^2 y_2^2 + y_1^2 w_2^2 + z_1^2 x_2^2 + x_1^2 z_2^2 \\
+w_1^2 z_2^2 + z_1^2 w_2^2 + x_1^2 y_2^2 + y_1^2 x_2^2
\end{aligned}
} \\[2ex]
& = \sqrt{
\begin{aligned}
w_1^2 (w_2^2 + x_2^2 + y_2^2 + z_2^2 ) \\
+x_1^2 (w_2^2 + x_2^2 + y_2^2 + z_2^2 ) \\
+y_1^2 (w_2^2 + x_2^2 + y_2^2 + z_2^2 ) \\
+z_1^2 (w_2^2 + x_2^2 + y_2^2 + z_2^2 )
\end{aligned}
} \\[2ex]
& = \sqrt{
(w_1^2 + x_1^2 + y_1^2 + z_1^2)(w_2^2 + x_2^2 + y_2^2 + z_2^2)
}
\end{aligned}
∥ q 1 × q 2 ∥ = ∥ ∥ [ w 1 ( x 1 y 1 z 1 ) ] × [ w 2 ( x 2 y 2 z 2 ) ] ∥ ∥ = ∥ ∥ ∥ ∥ ∥ ∥ ∥ ∥ ∥ ∥ ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ w 1 w 2 − x 1 x 2 − y 1 y 2 − z 1 z 2 w 1 x 2 + x 1 w 2 + y 1 z 2 − z 1 y 2 w 1 y 2 + y 1 w 2 + z 1 x 2 − x 1 z 2 w 1 z 2 + z 1 w 2 + x 1 y 2 − y 1 x 2 ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ ∥ ∥ ∥ ∥ ∥ ∥ ∥ ∥ ∥ ∥ = ( w 1 w 2 − x 1 x 2 − y 1 y 2 − z 1 z 2 ) 2 + ( w 1 x 2 + x 1 w 2 + y 1 z 2 − z 1 y 2 ) 2 + ( w 1 y 2 + y 1 w 2 + z 1 x 2 − x 1 z 2 ) 2 + ( w 1 z 2 + z 1 w 2 + x 1 y 2 − y 1 x 2 ) 2 = w 1 2 w 2 2 + x 1 2 x 2 2 + y 1 2 y 2 2 + z 1 2 z 2 2 + w 1 2 x 2 2 + x 1 2 w 2 2 + y 1 2 z 2 2 + z 1 2 y 2 2 + w 1 2 y 2 2 + y 1 2 w 2 2 + z 1 2 x 2 2 + x 1 2 z 2 2 + w 1 2 z 2 2 + z 1 2 w 2 2 + x 1 2 y 2 2 + y 1 2 x 2 2 = w 1 2 ( w 2 2 + x 2 2 + y 2 2 + z 2 2 ) + x 1 2 ( w 2 2 + x 2 2 + y 2 2 + z 2 2 ) + y 1 2 ( w 2 2 + x 2 2 + y 2 2 + z 2 2 ) + z 1 2 ( w 2 2 + x 2 2 + y 2 2 + z 2 2 ) = ( w 1 2 + x 1 2 + y 1 2 + z 1 2 ) ( w 2 2 + x 2 2 + y 2 2 + z 2 2 )
四元数乘积的模等于模的乘积:
∥ q 1 × q 2 ∥ = ( w 1 2 + x 1 2 + y 1 2 + z 1 2 ) ( w 2 2 + x 2 2 + y 2 2 + z 2 2 ) = ∥ q 1 ∥ 2 ∥ q 2 ∥ 2 = ∥ q 1 ∥ ∥ q 2 ∥ \begin{aligned}
\Vert {\bold{q_1} \times \bold{q_2}} \Vert & = \sqrt{
(w_1^2 + x_1^2 + y_1^2 + z_1^2)(w_2^2 + x_2^2 + y_2^2 + z_2^2)
} \\[2ex]
& = \sqrt{\Vert {\bold{q_1}} \Vert^2 \Vert {\bold{q_2}} \Vert^2} \\[2ex]
& = \sqrt{\Vert {\bold{q_1}} \Vert \Vert {\bold{q_2}} \Vert}
\end{aligned}
∥ q 1 × q 2 ∥ = ( w 1 2 + x 1 2 + y 1 2 + z 1 2 ) ( w 2 2 + x 2 2 + y 2 2 + z 2 2 ) = ∥ q 1 ∥ 2 ∥ q 2 ∥ 2 = ∥ q 1 ∥ ∥ q 2 ∥
四元数乘积的逆等于各个四元数的逆以相反的顺序相乘:
{ ( a b ) − 1 = b − 1 a − 1 ( q 1 q 2 ⋯ q n − 1 q n ) − 1 = q n − 1 q n − 1 − 1 ⋯ q 2 − 1 q 1 − 1 \begin{cases}
(\bold{a} \bold{b})^{-1} = \bold{b}^{-1} \bold{a}^{-1} \\
(\bold{q_1} \bold{q_2} \cdots \bold{q_{n-1}} \bold{q_{n}})^{-1} =
\bold{q_{n}}^{-1} \bold{q_{n-1}}^{-1} \cdots \bold{q_{2}}^{-1} \bold{q_{1}}^{-1}
\end{cases}
{ ( a b ) − 1 = b − 1 a − 1 ( q 1 q 2 ⋯ q n − 1 q n ) − 1 = q n − 1 q n − 1 − 1 ⋯ q 2 − 1 q 1 − 1
“扩展”一个标准 3D 点 ( x , y , z ) (x, y, z) ( x , y , z ) p = [ 0 , ( x , y , z ) ] \bold{p} = [0, (x, y, z)] p = [ 0 , ( x , y , z ) ] p \bold{p} p
设 q \bold{q} q q = [ cos ( θ / 2 ) , n cos ( θ / 2 ) ] q = [\cos{(\theta/2)}, \space \bold{n}\cos{(\theta/2)}] q = [ cos ( θ / 2 ) , n cos ( θ / 2 ) ]
其中,n \bold{n} n θ \theta θ
使用下式可使 3D 点 p \bold{p} p n \bold{n} n
p ′ = q p q − 1 \bold{p'} = \bold{q}\bold{p}\bold{q}^{-1}
p ′ = q p q − 1
将点 p \bold{p} p a \bold{a} a b \bold{b} b
p ′ = b ( a p a − 1 ) b − 1 = ( b a ) p ( a − 1 b − 1 ) = ( b a ) p ( b a ) − 1 \begin{aligned}
\bold{p'} &= \bold{b}(\bold{a}\bold{p}\bold{a}^{-1})\bold{b}^{-1} \\
&= (\bold{b}\bold{a})\bold{p}(\bold{a}^{-1}\bold{b}^{-1}) \\
&= (\bold{b}\bold{a})\bold{p}(\bold{b}\bold{a})^{-1}
\end{aligned}
p ′ = b ( a p a − 1 ) b − 1 = ( b a ) p ( a − 1 b − 1 ) = ( b a ) p ( b a ) − 1
先进行 a \bold{a} a b \bold{b} b b a \bold{b}\bold{a} b a
[ w 1 ( x 1 y 1 z 1 ) ] × [ w 2 ( x 2 y 2 z 2 ) ] = [ w 1 w 2 − x 1 x 2 − y 1 y 2 − z 1 z 2 w 1 x 2 + x 1 w 2 + z 1 y 2 − y 1 z 2 w 1 y 2 + y 1 w 2 + x 1 z 2 − z 1 x 2 w 1 z 2 + z 1 w 2 + y 1 x 2 − x 1 y 2 ] \begin{aligned}
& \begin{bmatrix} w_1 &(x_1 &y_1 &z_1) \end{bmatrix} \times \begin{bmatrix} w_2 &(x_2 &y_2 &z_2) \end{bmatrix} \\[2ex]
& =
\begin{bmatrix}
w_1w_2 - x_1x_2 - y_1y_2 - z_1z_2 \\[1.25ex] \hdashline
w_1x_2 + x_1w_2 + z_1y_2 - y_1z_2 \\[1.25ex]
w_1y_2 + y_1w_2 + x_1z_2 - z_1x_2 \\[1.25ex]
w_1z_2 + z_1w_2 + y_1x_2 - x_1y_2
\end{bmatrix}
\end{aligned}
[ w 1 ( x 1 y 1 z 1 ) ] × [ w 2 ( x 2 y 2 z 2 ) ] = ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ w 1 w 2 − x 1 x 2 − y 1 y 2 − z 1 z 2 w 1 x 2 + x 1 w 2 + z 1 y 2 − y 1 z 2 w 1 y 2 + y 1 w 2 + x 1 z 2 − z 1 x 2 w 1 z 2 + z 1 w 2 + y 1 x 2 − x 1 y 2 ⎦ ⎥ ⎥ ⎥ ⎥ ⎤
此时运算顺序相反:
p ′ = b − 1 ( a − 1 p a ) b = ( b − 1 a − 1 ) p ( a b ) = ( a b ) − 1 p ( a b ) \begin{aligned}
\bold{p'} &= \bold{b}^{-1}(\bold{a}^{-1}\bold{p}\bold{a})\bold{b} \\
&= (\bold{b}^{-1}\bold{a}^{-1})\bold{p}(\bold{a}\bold{b}) \\
&= (\bold{a}\bold{b})^{-1}\bold{p}(\bold{a}\bold{b})
\end{aligned}
p ′ = b − 1 ( a − 1 p a ) b = ( b − 1 a − 1 ) p ( a b ) = ( a b ) − 1 p ( a b )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 Quaternion Quaternion::operator *(const Quaternion& a) const { Quaternion result; result.w = w * a.w - x * a.x - y * a.y - z * a.z; result.x = w * a.x + x * a.w + z * a.y - y * a.z; result.y = w * a.y + y * a.w + x * a.z - z * a.x; result.z = w * a.z + z * a.w + y * a.x - x * a.y; return result; } Quaternion& Quaternion::operator *=(const Quaternion& a) { *this = *this * a; return *this ; }
利用四元数的乘法和逆,计算两个四元数的“差值”。“差值”被定义为一个方位到另一个方位的角位移。
给定方位 a \bold{a} a b \bold{b} b a \bold{a} a b \bold{b} b d \bold{d} d
d a = b \bold{d}\bold{a} = \bold{b}
d a = b
可推出:
( d a ) a − 1 = b a − 1 d = b a − 1 \begin{aligned}
(\bold{d}\bold{a})\bold{a}^{-1} &= \bold{b}\bold{a}^{-1} \\[1.5ex]
\bold{d} &= \bold{b}\bold{a}^{-1}
\end{aligned}
( d a ) a − 1 d = b a − 1 = b a − 1
q 1 ⋅ q 2 = [ w 1 v 1 ] ⋅ [ w 2 v 2 ] = w 1 w 2 + v 1 ⋅ v 2 = [ w 1 ( x 1 y 1 z 1 ) ] ⋅ [ w 2 ( x 2 y 2 z 2 ) ] = w 1 w 2 + x 1 x 2 + y 1 y 2 + z 1 z 2 \begin{aligned}
\bold{q_1} \cdot \bold{q_2} &= \begin{bmatrix} w_1 &\bold{v_1} \end{bmatrix} \cdot \begin{bmatrix} w_2 &\bold{v_2} \end{bmatrix} \\[1.25ex]
&= w_1w_2 + \bold{v_1} \cdot \bold{v_2} \\[2ex]
&= \begin{bmatrix} w_1 &(x_1 &y_1 &z_1) \end{bmatrix} \cdot \begin{bmatrix} w_2 &(x_2 &y_2 &z_2) \end{bmatrix} \\[1.25ex]
&= w_1w_2 + x_1x_2 + y_1y_2 + z_1z_2
\end{aligned}
q 1 ⋅ q 2 = [ w 1 v 1 ] ⋅ [ w 2 v 2 ] = w 1 w 2 + v 1 ⋅ v 2 = [ w 1 ( x 1 y 1 z 1 ) ] ⋅ [ w 2 ( x 2 y 2 z 2 ) ] = w 1 w 2 + x 1 x 2 + y 1 y 2 + z 1 z 2
和向量点乘一样,结果是标量:
对于单位四元数 a \bold{a} a b \bold{b} b − 1 ⩽ a ⋅ b ⩽ 1 -1 \leqslant \bold{a} \cdot \bold{b} \leqslant 1 − 1 ⩽ a ⋅ b ⩽ 1
由于四元数的正负号不影响其代表的角位移,因此结果往往只关心其绝对值 ∣ a ⋅ b ∣ | \bold{a} \cdot \bold{b} | ∣ a ⋅ b ∣
1 2 3 4 5 6 7 8 9 float dotProduct (const Quaternion& a, const Quaternion& b) return a.w * b.w + a.x * b.x + a.y * b.y + a.z * b.z; }
几何解释 :
四元数点乘的几何解释类似于向量点乘的几何解释。
四元数点乘的绝对值 ∣ a ⋅ b ∣ | \bold{a} \cdot \bold{b} | ∣ a ⋅ b ∣ a \bold{a} a b \bold{b} b
重写四元数定义,引入一个新的变量 α = θ / 2 \alpha = \theta/2 α = θ / 2
q = [ cos α n sin α ] = [ cos α n x sin α n y sin α n z sin α ] \begin{aligned}
\bold{q} &= \begin{bmatrix} \cos{\alpha} &\bold{n} \sin{\alpha} \end{bmatrix} \\[1.25ex]
&= \begin{bmatrix} \cos{\alpha} &\bold{n}_x \sin{\alpha} &\bold{n}_y \sin{\alpha} &\bold{n}_z \sin{\alpha} \end{bmatrix}
\end{aligned}
q = [ cos α n sin α ] = [ cos α n x sin α n y sin α n z sin α ]
log q = log ( [ cos α n sin α ] ) ≡ [ 0 α n ] \begin{aligned}
\log{\bold{q}} &= \log{(\begin{bmatrix} \cos{\alpha} &\bold{n} \sin{\alpha} \end{bmatrix})} \\[1.25ex]
&\equiv \begin{bmatrix} 0 &\alpha \bold{n} \end{bmatrix}
\end{aligned}
log q = log ( [ cos α n sin α ] ) ≡ [ 0 α n ]
其中的结果 [ 0 α n ] \begin{bmatrix} 0 &\alpha \bold{n} \end{bmatrix} [ 0 α n ]
四元数的对数运算中,有如下的映射关系:
( w , v ) ↦ log ( θ , n ) (w,\bold{v}) \xmapsto{\log} (\theta,\bold{n})
( w , v ) log ( θ , n )
令四元数 p \bold{p} p
p = [ 0 α n ] = [ 0 ( α n x α n y α n z ) ] \begin{aligned}
\bold{p} &= \begin{bmatrix} 0 &\alpha \bold{n} \end{bmatrix} \\[1.25ex]
&= \begin{bmatrix} 0 &(\alpha \bold{n}_x &\alpha \bold{n}_y &\alpha \bold{n}_z) \end{bmatrix}
\end{aligned}
p = [ 0 α n ] = [ 0 ( α n x α n y α n z ) ]
指数定义为:
e p = exp p = exp ( [ 0 α n ] ) ≡ [ cos α n sin α ] \begin{aligned}
e^{\bold{p}} = \exp{\bold{p}} &= \exp{(\begin{bmatrix} 0 &\alpha \bold{n} \end{bmatrix})} \\[1.25ex]
&\equiv \begin{bmatrix} \cos{\alpha} &\bold{n} \sin{\alpha} \end{bmatrix}
\end{aligned}
e p = exp p = exp ( [ 0 α n ] ) ≡ [ cos α n sin α ]
根据定义,exp p \exp{\bold{p}} exp p
四元数指数运算为四元数对数运算的逆运算:
exp ( log q ) = q \exp{(\log{\bold{q}})} = \bold{q}
exp ( log q ) = q
四元数的指数运算中,有如下的映射关系:
( θ , n ) ↦ exp ( w , v ) (\theta,\bold{n}) \xmapsto{\exp} (w,\bold{v})
( θ , n ) exp ( w , v )
k q = k [ w v ] = [ k w k v ] = k [ w ( x y z ) ] = [ k w ( k x k y k z ) ] \begin{aligned}
k\bold{q} &= k \begin{bmatrix} w &\bold{v} \end{bmatrix} = \begin{bmatrix} kw &k\bold{v} \end{bmatrix} \\[1.5ex]
&= k\begin{bmatrix} w &(x &y &z) \end{bmatrix} = \begin{bmatrix} kw &(kx &ky &kz) \end{bmatrix}
\end{aligned}
k q = k [ w v ] = [ k w k v ] = k [ w ( x y z ) ] = [ k w ( k x k y k z ) ]
四元数作为底数,记作 q t \bold{q}^t q t
实数求幂:
a 0 = 1 a^0 = 1 a 0 = 1 a 1 = a a^1 = a a 1 = a a a a 当 t t t 0 0 0 1 1 1 a t a^t a t 1 1 1 a a a
四元数求幂的意义类似于实数求幂:
q 0 = [ 1 , 0 ] \bold{q}^0 = [1,\space\bold{0}] q 0 = [ 1 , 0 ] q 1 = q \bold{q}^1 = \bold{q} q 1 = q 当 t t t 0 0 0 1 1 1 q t \bold{q}^t q t [ 1 , 0 ] [1,\space\bold{0}] [ 1 , 0 ] q \bold{q} q
NOTE :
四元数表示一个角位移,同时 角位移的叠加 又是通过四元数相乘的形式;
显然,导致在这样的变化过程中,[ 1 , 0 ] → q [1,\space\bold{0}] \to \bold{q} [ 1 , 0 ] → q
可以通过对四元数求幂从角位移中抽取“一部分”,并且 t t t [ 0 , 1 ] [0,\space 1] [ 0 , 1 ]
例如 :
四元数 q \bold{q} q
q 1 / 3 \bold{q}^{1/3} q 1 / 3 q \bold{q} q 1 / 3 1/3 1 / 3 q 2 \bold{q}^2 q 2 q \bold{q} q 2 2 2
假设四元数 q \bold{q} q n \bold{n} n 30 ° 30 \degree 3 0 °
q 1 / 3 \bold{q}^{1/3} q 1 / 3 n \bold{n} n 10 ° 10 \degree 1 0 ° q 2 \bold{q}^2 q 2 n \bold{n} n 60 ° 60 \degree 6 0 ° q − 1 / 3 \bold{q}^{-1/3} q − 1 / 3 n \bold{n} n 10 ° 10 \degree 1 0 °
特别地 :
四元数表示角位移时使用最短圆弧,不能 “ 绕圈 ” 。
假设四元数 q \bold{q} q n \bold{n} n 30 ° 30 \degree 3 0 °
q 8 \bold{q}^{8} q 8 n \bold{n} n 240 ° 240 \degree 2 4 0 ° 120 ° 120 \degree 1 2 0 °
显然,向一个方向旋转 240 ° 240 \degree 2 4 0 ° 120 ° 120 \degree 1 2 0 ° q 8 \bold{q}^{8} q 8 q − 4 \bold{q}^{-4} q − 4
但是进一步的指数运算的代数公式 ( a s ) t = a s t (a^s)^t = a^{st} ( a s ) t = a s t
例如:
{ ( q 8 ) 1 / 2 ≠ q 4 ( q 8 ) 1 / 2 = q − 2 \begin{cases}
(\bold{q}^{8})^{1/2} \ne \bold{q}^{4} \\
(\bold{q}^{8})^{1/2} = \bold{q}^{-2}
\end{cases}
{ ( q 8 ) 1 / 2 = q 4 ( q 8 ) 1 / 2 = q − 2
( q 8 ) 1 / 2 (\bold{q}^{8})^{1/2} ( q 8 ) 1 / 2 n \bold{n} n 120 ° 120 \degree 1 2 0 ° n \bold{n} n 60 ° 60 \degree 6 0 °
四元数求幂的数学定义 :
q t = exp ( t log q ) \bold{q}^t = \exp{(t\log{\bold{q}})}
q t = exp ( t log q )
通过四元数的指数运算和对数运算的映射关系来体现其中系数 t t t
( w , v ) ↦ log ( θ , n ) ↦ t ( t θ , n ) ↦ exp ( w ′ , v ′ ) (w,\bold{v}) \xmapsto{\log} (\theta,\bold{n}) \xmapsto{t} (t\theta,\bold{n}) \xmapsto{\exp} (w',\bold{v'})
( w , v ) log ( θ , n ) t ( t θ , n ) exp ( w ′ , v ′ )
其结果 q t = ( w ′ , v ′ ) \bold{q}^t = (w',\bold{v'}) q t = ( w ′ , v ′ ) q = ( w , v ) \bold{q} = (w,\bold{v}) q = ( w , v ) t t t
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 Quaternion pow (const Quaternion& q, float exponent) { if (fabs (q.w) > .9999 f) { return q; } float alpha = acos (q.w); float newAlpha = alpha * exponent; Quaternion result; result.w = cos (newAlpha); float mult = sin (newAlpha) / sin (alpha); result.x = q.x * mult; result.y = q.y * mult; result.z = q.z * mult; return result; }
球面线性插值 (S pherical L inear Interp olation):在两个四元数间进行平滑插值。
s l e r p slerp s l e r p q 0 \bold{q}_0 q 0 q 1 \bold{q}_1 q 1 插值参数设为变量 t t t t t t 0 0 0 1 1 1
s l e r p ( q 0 , q 1 , t ) slerp(\bold{q}_0,\space \bold{q}_1,\space t) s l e r p ( q 0 , q 1 , t ) q 0 \bold{q}_0 q 0 q 1 \bold{q}_1 q 1
标准线性插值公式 :
{ Δ a = a 1 − a 0 l e r p ( a 0 , a 1 , t ) = a 0 + t Δ a \begin{cases}
\Delta a = a_1 - a_0 \\[1.5ex]
lerp(a_0,a_1,t) = a_0 + t \Delta a
\end{cases}
⎩ ⎨ ⎧ Δ a = a 1 − a 0 l e r p ( a 0 , a 1 , t ) = a 0 + t Δ a
标准线性插值公式从 a 0 a_0 a 0 a 0 a_0 a 0 a 1 a_1 a 1 t t t
计算两个值的差 Δ a \Delta a Δ a
取得差的一部分 t Δ a t \Delta a t Δ a
在初始值 a 0 a_0 a 0
球面线性插值公式 :
s l e r p ( q 0 , q 1 , t ) = ( q 1 q 0 − 1 ) t q 0 slerp(\bold{q}_0,\space \bold{q}_1,\space t) = (\bold{q}_1\bold{q}_0^{-1})^t\bold{q}_0
s l e r p ( q 0 , q 1 , t ) = ( q 1 q 0 − 1 ) t q 0
计算两个值的差 : Δ q = q 1 q 0 − 1 \Delta\bold{q} = \bold{q}_1\bold{q}_0^{-1} Δ q = q 1 q 0 − 1
计算差的一部分 :即为 Δ q t \Delta\bold{q}^t Δ q t
在开始值上加上差的一部分 :使用四元数乘法组合角位移 Δ q t q 0 \Delta\bold{q}^t\bold{q}_0 Δ q t q 0
在 4D 空间中解释四元数,由于考虑的四元数都是单位四元数,所以可以将它们都看做是 “ 存在 ” 于一个 4D “ 球面 ” 上。
slerp 的基本思想 :沿着 4D 球面上连接两个四元数的弧插值。
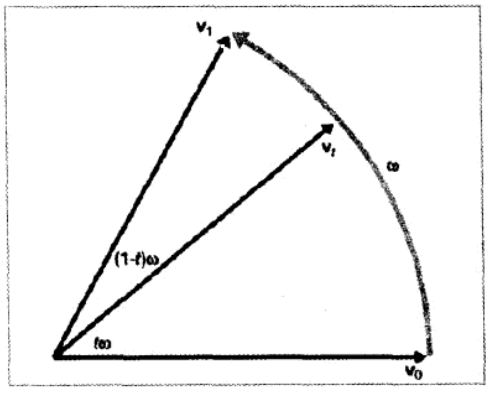
可以把这种思想表现在平面上,设两个 2D 向量 v 0 \bold{v}_0 v 0 v 1 \bold{v}_1 v 1
计算 v t \bold{v}_t v t v 0 \bold{v}_0 v 0 v t \bold{v}_t v t
设 ω \omega ω v 0 \bold{v}_0 v 0 v t \bold{v}_t v t v t \bold{v}_t v t t ω t\omega t ω
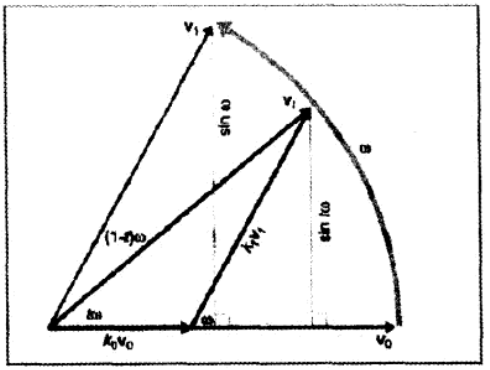
将 v t \bold{v}_t v t v 0 \bold{v}_0 v 0 v 1 \bold{v}_1 v 1 k 0 k_0 k 0 k 1 k_1 k 1
v 0 = k 0 v 0 + k 1 v 1 \bold{v}_0 = k_0 \bold{v}_0 + k_1 \bold{v}_1
v 0 = k 0 v 0 + k 1 v 1
可以用基本几何学求出 k 0 k_0 k 0 k 1 k_1 k 1
{ k 1 = sin t ω sin ω k 0 = sin ( 1 − t ) ω sin ω \begin{cases}
k_1 = \cfrac{\sin{t\omega}}{\sin{\omega}} \\[3ex]
k_0 = \cfrac{\sin{(1 - t)\omega}}{\sin{\omega}}
\end{cases}
⎩ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎧ k 1 = sin ω sin t ω k 0 = sin ω sin ( 1 − t ) ω
v t \bold{v}_t v t
v t = k 0 v 0 + k 1 v 1 v t = sin ( 1 − t ) ω sin ω v 0 + sin t ω sin ω v 1 \begin{aligned}
& \bold{v}_t = k_0 \bold{v}_0 + k_1 \bold{v}_1 \\[3ex]
& \bold{v}_t = \cfrac{\sin{(1 - t)\omega}}{\sin{\omega}} \bold{v}_0 + \cfrac{\sin{t\omega}}{\sin{\omega}} \bold{v}_1
\end{aligned}
v t = k 0 v 0 + k 1 v 1 v t = sin ω sin ( 1 − t ) ω v 0 + sin ω sin t ω v 1
而四元数的 slerp 有类似形式:
s l e r p ( q 0 , q 1 , t ) = sin ( 1 − t ) ω sin ω q 0 + sin t ω sin ω q 1 slerp(\bold{q}_0,\space \bold{q}_1,\space t) = \cfrac{\sin{(1 - t)\omega}}{\sin{\omega}} \bold{q}_0 + \cfrac{\sin{t\omega}}{\sin{\omega}} \bold{q}_1
s l e r p ( q 0 , q 1 , t ) = sin ω sin ( 1 − t ) ω q 0 + sin ω sin t ω q 1
可以用点乘来计算两个四元数间的 “ 角度 ω \omega ω cos ω \cos{\omega} cos ω
NOTE :
四元数 q \bold{q} q − q -\bold{q} − q 解决方法 :选择 q 0 \bold{q}_0 q 0 q 1 \bold{q}_1 q 1 q 0 ⋅ q 1 \bold{q}_0 \cdot \bold{q}_1 q 0 ⋅ q 1
要考虑的是如果 q 0 \bold{q}_0 q 0 q 1 \bold{q}_1 q 1 sin θ \sin{\theta} sin θ 0 0 0 解决方法 :当 sin θ \sin{\theta} sin θ 简单的线性插值 。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 Quaternion slerp (const Quaternion& q0, const Quaternion& q1, float t) { if (t <= 0.0f ) return q0; if (t >= 1.0f ) return q1; float cosOmega = dotProduct(q0, q1); float q1w = q1.w; float q1x = q1.x; float q1y = q1.y; float q1z = q1.z; if (cosOmega < 0.0f ) { q1w = -q1w; q1x = -q1x; q1y = -q1y; q1z = -q1z; cosOmega = -cosOmega; } assert(cosOmega < 1.1f ); float k0, k1; if (cosOmega > 0.9999f ) { k0 = 1.0f - t; k1 = t; } else { float sinOmega = sqrt (1.0f - cosOmega * cosOmega); float omega = atan2 (sinOmega, cosOmega); float oneOverSinOmega = 1.0f / sinOmega; k0 = sin ((1.0f - t) * omega) * oneOverSinOmega; k1 = sin (t * omega) * oneOverSinOmega; } Quaternion result; result.x = k0 * q0.x + k1 * q1x; result.y = k0 * q0.y + k1 * q1y; result.z = k0 * q0.z + k1 * q1z; result.w = k0 * q0.w + k1 * q1w; return result; }
s l e r p slerp s l e r p s l e r p slerp s l e r p
类似于基本几何学中的线性插值,控制点之间是以直线连接,这会导致控制点上会有 不连续性 。
使用 s q u a d squad s q u a d S pherical and Quad rangle) 描绘控制点间的路径。
设 控制点 由四元数序列所定义:
q 0 , q 2 , q 3 , ⋯ , q n − 2 , q n − 1 , q n \bold{q}_0,\bold{q}_2,\bold{q}_3,\cdots,\bold{q}_{n-2},\bold{q}_{n-1},\bold{q}_{n}
q 0 , q 2 , q 3 , ⋯ , q n − 2 , q n − 1 , q n
引进一个“辅助”四元数 s i \bold{s}_i s i
s i = exp ( − log ( q i + 1 q i − 1 ) + log ( q i − 1 q i − 1 ) 4 ) q i = ( Δ q [ i → i − 1 ] Δ q [ i → i + 1 ] ) − 1 4 q i \begin{aligned}
\bold{s}_i &= \exp{\left( -\cfrac{\log{(\bold{q}_{i+1}\bold{q}_{i}^{-1})} + \log{(\bold{q}_{i-1}\bold{q}_{i}^{-1})} }{4} \right)}\bold{q}_{i} \\[3ex]
&= (\Delta \bold{q}_{[i \to i-1]} \Delta \bold{q}_{[i \to i+1]} )^{-\frac{1}{4}} \bold{q}_{i}
\end{aligned}
s i = exp ( − 4 log ( q i + 1 q i − 1 ) + log ( q i − 1 q i − 1 ) ) q i = ( Δ q [ i → i − 1 ] Δ q [ i → i + 1 ] ) − 4 1 q i
NOTE :s i \bold{s}_i s i q i − 1 \bold{q}_{i-1} q i − 1 q i + 1 \bold{q}_{i+1} q i + 1 s 1 \bold{s}_1 s 1 s n \bold{s}_n s n
换言之,曲线从 q 2 \bold{q}_{2} q 2 q n − 1 \bold{q}_{n-1} q n − 1 q 1 \bold{q}_{1} q 1 q n \bold{q}_{n} q n q 1 \bold{q}_{1} q 1 q n \bold{q}_{n} q n q 0 \bold{q}_{0} q 0 q n + 1 \bold{q}_{n+1} q n + 1
{ q 0 = q 1 q n + 1 = q n \begin{cases}
\bold{q}_{0} = \bold{q}_{1} \\
\bold{q}_{n+1} = \bold{q}_{n}
\end{cases}
{ q 0 = q 1 q n + 1 = q n
给定四个相邻的控制点 q i − 1 , q i , q i + 1 , q i + 2 \bold{q}_{i-1},\bold{q}_{i},\bold{q}_{i+1},\bold{q}_{i+2} q i − 1 , q i , q i + 1 , q i + 2 s q u a d squad s q u a d q i , q i + 1 \bold{q}_{i},\bold{q}_{i+1} q i , q i + 1
“squad” 函数 :
同时还需要引入一个插值变量 h h h h h h 0 0 0 1 1 1 s q u a d squad s q u a d q i \bold{q}_{i} q i q i + 1 \bold{q}_{i+1} q i + 1
整条插值曲线能分段应用 s q u a d squad s q u a d
s q u a d ( q i , q i + 1 , s i , s i + 1 , h ) = s l e r p ( s l e r p ( q i , q i + 1 , h ) , s l e r p ( s i , s i + 1 , h ) , 2 h ( 1 − h ) ) squad(\bold{q}_{i},\bold{q}_{i+1},\bold{s}_{i},\bold{s}_{i+1},h) =
slerp(\space slerp(\bold{q}_{i},\bold{q}_{i+1},h),\space slerp(\bold{s}_{i},\space \bold{s}_{i+1},h),\space 2h(1-h)\space )
s q u a d ( q i , q i + 1 , s i , s i + 1 , h ) = s l e r p ( s l e r p ( q i , q i + 1 , h ) , s l e r p ( s i , s i + 1 , h ) , 2 h ( 1 − h ) )
参考视频 :