1. 图形学的依赖学科
2. 向量
向量的定义,标准化,求和,坐标表示,求长度等知识
(图形学上默认以列向量表示)
2.1 点乘
2.1.1 定义和运算律
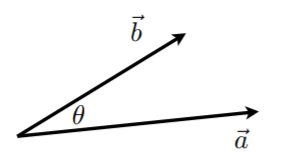
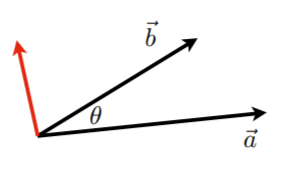
a⋅bcosθ=∥a∥∥b∥cosθ=∥a∥∥b∥a⋅b
cosθ=a^⋅b^
2.1.2 坐标的运算以及作用
找夹角和找投影
a⋅b=(xaya)⋅(xbyb)=xaxb+yayb
a⋅b=⎝⎛xayaza⎠⎞⋅⎝⎛xbybzb⎠⎞=xaxb+yayb+zazb
2.1.3 点乘的作用
- 两个向量之间的接近程度
- 分解向量
- 根据点乘结果正负判断前后
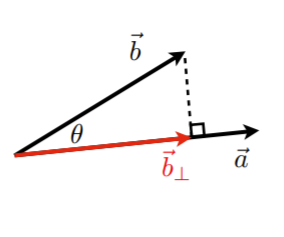
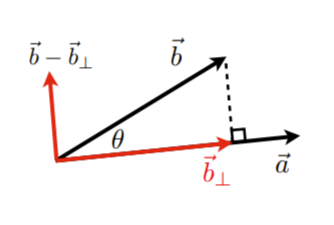
- b⊥ :b 在 a 上的投影
- b⊥ 必须沿着 a (或者沿着 a^ )
- 对应的模 k
- k=∥b⊥∥=∥b^∥cosθ
2.2 叉乘
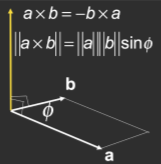
- 叉乘的定义和运算律
- 右手定则判断叉乘方向
- 这节课都是右手坐标系,OpenGL是左手坐标系
2.2.1 叉乘的坐标计算
x×yy×xy×zz×yz×xx×z=+z=−z=+x=−x=+y=−y
2.2.2 叉乘的计算
a×ba×aa×(b+c)a×(kb)=−b×a=0=a×b+a×c=k(a×b)
a×b=⎝⎛yazb−ybzazaxb−xazbxayb−yaxb⎠⎞
a×b=A∗b=⎝⎛0za−ya−za0xaya−xa0⎠⎞⎝⎛xbybzb⎠⎞
2.2.3 叉乘的作用
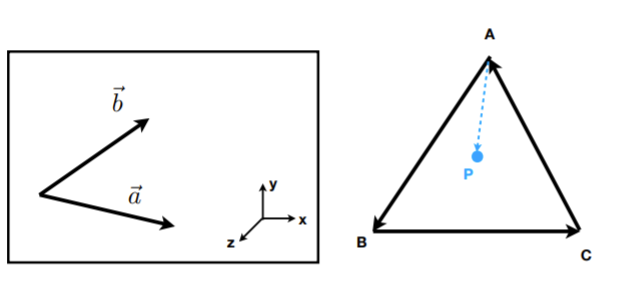
- 判断左右:利用叉乘结果的正负
- 判断内外:P点一直在三条边的左边/右边
3. 矩阵
- 矩阵的定义
- 乘法
- 运算律:结合律,分配律,没有交换律
- 转置:行列互换, aij 变成 aji
- 逆:相乘为单位矩阵





