1. Blinn-Phong 反射模型

镜面反射高光（Specular highlight）
漫反射（Diffuse reflection）
间接光照（Ambient lighting）

1.1 漫反射项

独立于视图方向的着色。

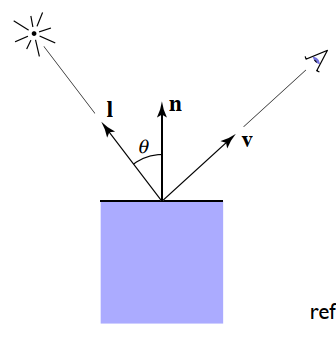
L_d = k_d (I/r^2) \max (0,\bold{n} \cdot \bold{l})

$L_d$ ：漫反射的反射光。
$k_d$ ：漫反射系数，向四周漫射的光通量与总的反射光通量之比。
$(I/r^2)$ ：在着色点处的光的能量（该式根据光的能量衰减模型来获得）。
$\max (0,\bold{n} \cdot \bold{l})$ ：着色点接收到的光的能量（根据兰伯特余弦定律，特别地，当余弦为负数时，能量为零）。

1.2 镜面反射项（Blinn-Phong 模型）

强度取决于视图方向

明亮处接近镜面反射方向

观察到“高光”的条件：观察方向与镜面反射方向接近时，即 $\bold{v}$ 和 $\bold{R}$ 足够接近。

$\bold{v}$ 与镜面反射方向接近 $\Leftrightarrow$ 半程向量（half vector）接近法向量

使用用单位向量之间的点积测定“接近”

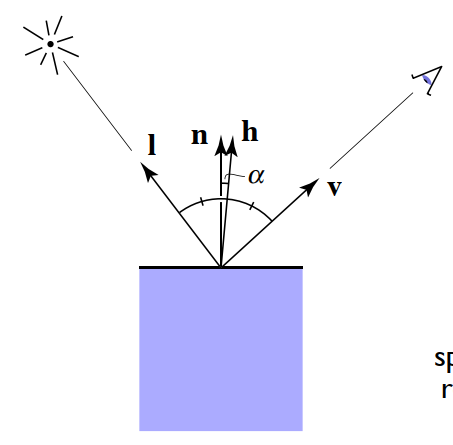
\begin{aligned} \bold{h} &= bisector(\bold{v},\bold{l}) \\ &= \cfrac{\bold{v}+\bold{l}}{\Vert{\bold{v}+\bold{l}}\Vert} \\[4ex] L_s &= k_s (I/r^2)\max(0,\cos{\alpha})^p \\ &= k_s (I/r^2)\max(0,\bold{n} \cdot \bold{h})^p \end{aligned}

$\bold{h}$ ：半程向量，向量 $\bold{v}$ 和 $\bold{l}$ 的角平分线。
$L_s$ ：镜面反射光。
$k_s$ ：镜面反射系数，通常设置为“白色光”。
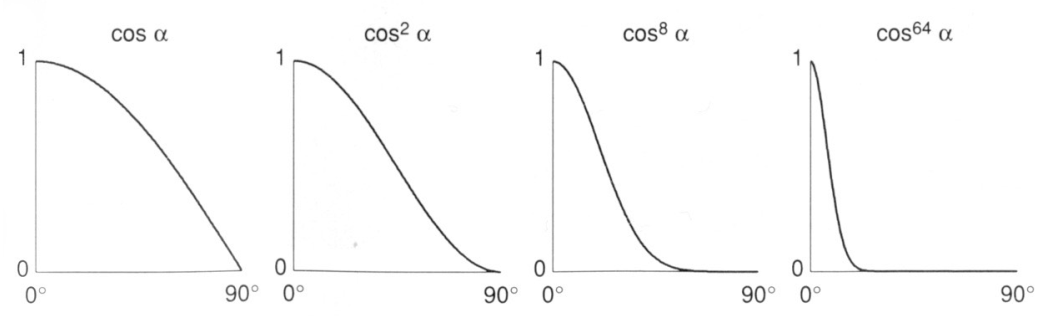
$p$ ：随着指数 p 的增加，反射波瓣变窄，此时只有“足够接近”时才会产生镜面反射。

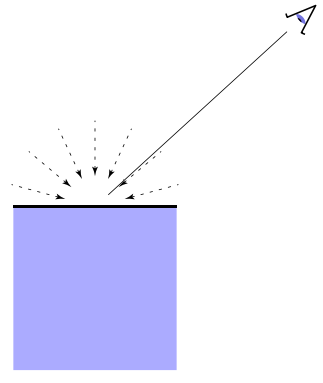
1.3 环境光照项

该部分着色不依赖于任何条件

添加恒定颜色，表现出忽略的照明和填充黑色阴影；
是一种近似的/假的。

L_a = k_a I_a

$L_a$ ：反射环境光。
$k_a$ ：环境光系数，该着色点的颜色。

1.4 实例

\begin{aligned} L &= L_a + L_d + L_s \\ &= k_a I_a + k_d (I/r^2) \max (0,\bold{n} \cdot \bold{l}) + k_s (I/r^2)\max(0,\bold{n} \cdot \bold{h})^p \end{aligned}

2. 着色频率（Shading Frequencies）

2.1 平面着色（flat shading）

为每个三角形平面进行着色

将三角形面视为单位平面，对应一个法向量。
该方法不适合光滑表面。

2.2 Gouraud 着色（Gouraud shading）

先计算每个顶点的着色；
在三角形上根据对应的三个顶点的着色进行插值获得三角形的颜色；
每个顶点都有其对应的一个法向量。

2.3 Phong 着色（Phong shading）

在 Gouraud 着色的基础上，对三角形内部的每个像素进行插值着色。
在每个三角形上插入法向量。
计算每个像素的完全着色模型。
注意该处指的是一种着色频率，不是 Blinn-Phong 反射模型。

2.4 三种着色频率

NOTE：当几何面数较大，模型足够复杂的情况下，可以使用相对简单的着色模型。

2.5 定义每个顶点的法向量

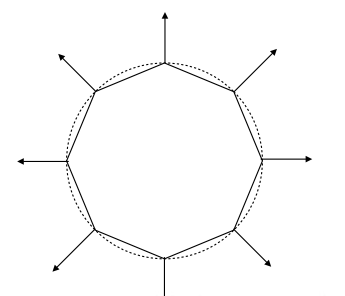
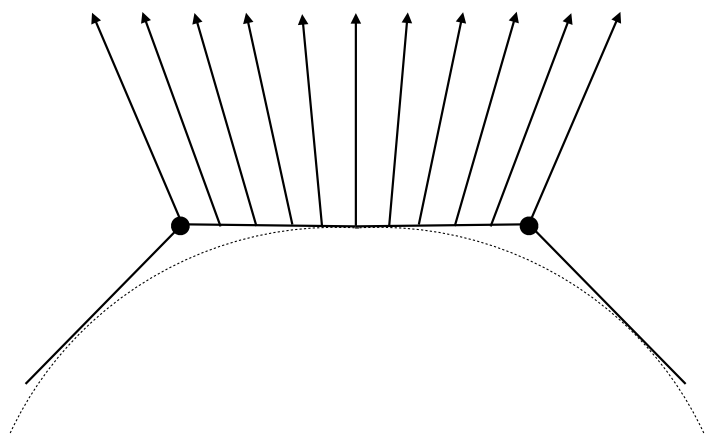
最好的方法是从基础几何体获取顶点法线

例如，考虑一个球体

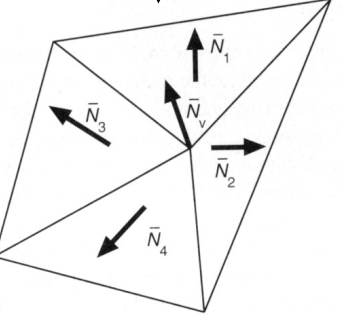
一般情况下，从三角形面推断顶点法线

简单方案：平均周围面法线

N_v = \cfrac{\sum_{i}{N_i}}{\Vert{\sum_{i}{N_i}}\Vert}

顶点法线的重心插值
记得标准化插值方向

3. 实时渲染管线

3.1 着色代码

程序顶点和像素处理阶段。
代码中仅需要描述单个顶点（或像素）上的操作。

GLSL片段着色器程序示例

uniform sampler2D myTexture;
// 程序参数
uniform vec3 lightDir;
// 程序参数
varying vec2 uv;
// 针对每个像素的对应值，内部通过光栅化
varying vec3 norm;
// 针对每个像素的对应值，内部通过光栅化

void diffuseShader()
{
    vec3 kd;
    kd = texture2d(myTexture, uv);
    // 光反射系数，来自纹理的材质颜色
    kd *= clamp(dot(–lightDir, norm), 0.0, 1.0);
    // 朗伯着色模型
    gl_FragColor = vec4(kd, 1.0);
    // 输出像素的着色
}

着色器功能每个片段执行一次。
在当前片段的屏幕样本位置输出表面颜色。
此着色器此时执行纹理查找以获取表面的材质颜色，然后执行漫反射照明计算。

3.2 参考网址

http://shadertoy.com/view/ld3Gz2

镜之国的爱丽丝

08 - 着色02（着色、管线）