镜之国的爱丽丝
0%

09 - 着色03（纹理映射）

发表于 更新于 分类于 ，

1. 纹理映射

Ld=kd∗(I/r2)∗(n⋅l)L_d = k_d * (I/r^2) * (\bold{n} \cdot \bold{l})

在着色过程中，很多时候需要定义某个物体上的各个点的漫反射系数 kdk_d ，即对应的颜色。

  • 指定顶点处的值（找到三角形的点对应在纹理上的点）
  • 通过三角形获得平滑变化的值

2. 重心坐标

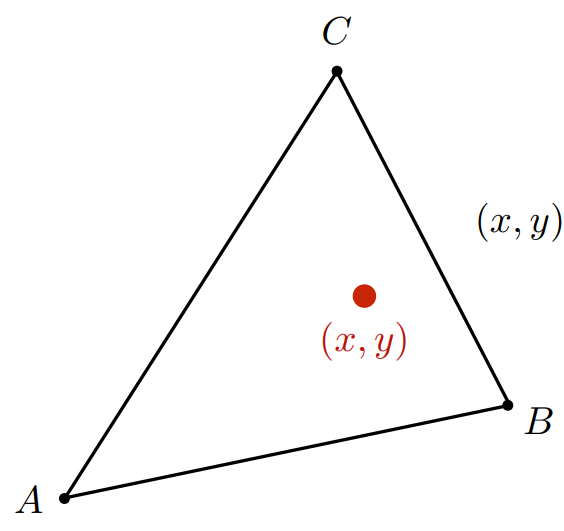
screenShot.png

三角形的坐标系 (α,β,γ)(\alpha,\beta,\gamma)

三角形平面上任意一点的坐标 (x,y)(x,y) 都可以用三个顶点的坐标的线性组合表示。

(x,y)=αA+βB+γCα+β+γ=1\begin{aligned} (x,y) = &\alpha A + \beta B + \gamma C \\ &\alpha + \beta + \gamma = 1 \end{aligned}

NOTE ：如果所有三个坐标都不为负，则该点在三角形内。

2.1 几何视点 - 比例区域

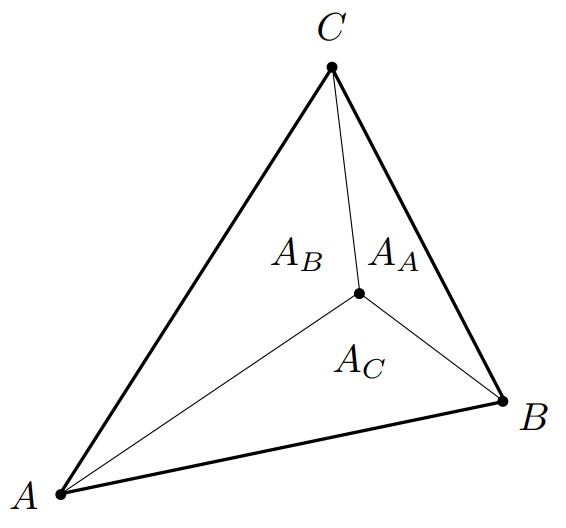
screenShot.png

α=AAAA+AB+ACβ=ABAA+AB+ACγ=ACAA+AB+AC\begin{aligned} \alpha = \cfrac{A_A}{A_A + A_B + A_C} \\ \beta = \cfrac{A_B}{A_A + A_B + A_C} \\ \gamma = \cfrac{A_C}{A_A + A_B + A_C} \end{aligned}

2.2 三角形自己的重心

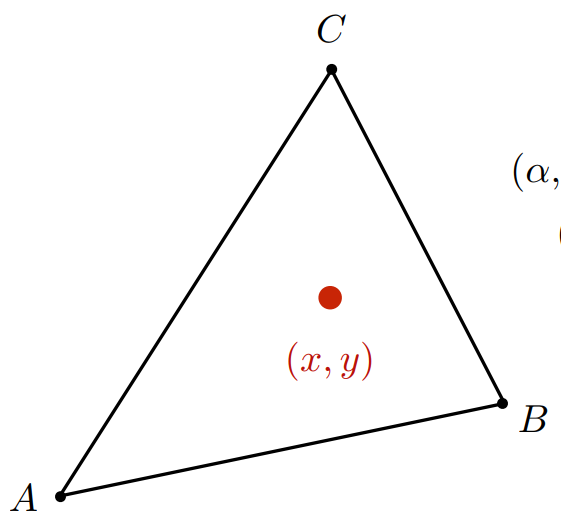
screenShot.png

(α,β,γ)=(13,13,13)(x,y)=13A+13B+13C\begin{aligned} (\alpha,\beta,\gamma) &= (\cfrac{1}{3},\cfrac{1}{3},\cfrac{1}{3}) \\[2ex] (x,y) &= \cfrac{1}{3} A + \cfrac{1}{3} B + \cfrac{1}{3} C \end{aligned}

2.3 重心坐标计算公式

α=−(x−xB)(yC−yB)+(y−yB)(xC−xB)−(xA−xB)(yC−yB)+(yA−yB)(xC−xB)β=−(x−xC)(yA−yC)+(y−yC)(xA−xC)−(xB−xC)(yA−yC)+(yB−yC)(xA−xC)γ=1−α−β\begin{aligned} \alpha &= \cfrac{-(x - x_B)(y_C - y_B) + (y - y_B)(x_C - x_B)} {-(x_A - x_B)(y_C - y_B) + (y_A - y_B)(x_C - x_B)} \\[2ex] \beta &= \cfrac{-(x - x_C)(y_A - y_C) + (y - y_C)(x_A - x_C)} {-(x_B - x_C)(y_A - y_C) + (y_B - y_C)(x_A - x_C)} \\[2ex] \gamma &= 1 - \alpha - \beta \end{aligned}

可以使用重心坐标对三角形进行在顶点上的线性插值

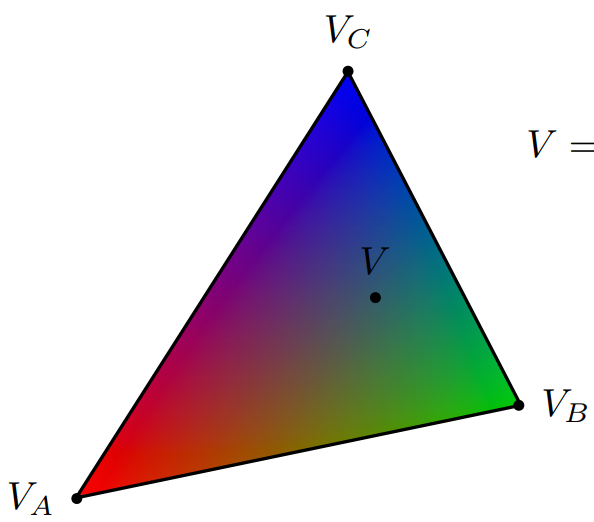
screenShot.png

V=αVA+βVB+γVCV = \alpha V_A + \beta V_B + \gamma V_C

其中属性 VAV_A ， VBV_B ， VCV_C 可以是位置，纹理坐标，颜色（图中所示），法线，深度，材质属性…

1
2
3
4
for each 光栅化屏幕样本 (x,y): \\ 通常是一个像素的中心
    (u,v) = 在 (x,y) 处评估纹理坐标
    texColor = texture.sample(u,v);  \\ 使用重心坐标
    sample's color = texColor;  \\ 通常是漫反射的反射率Kd（回想一下Blinn-Phong反射率模型）

3. 纹理过小

当纹理图片过小时，应用后会因为纹理分辨率不足导致图片失真。

纹理元素、纹素（texel） ：纹理上的像素。

screenShot.png

3.1 双线性插值（Bilinear Interpolation）

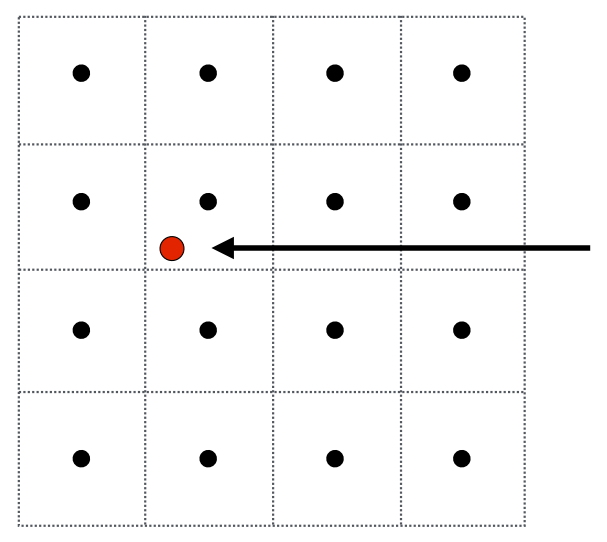
screenShot.png

  • 某个像素映射在非整数的位置，即图中红点，需要在红点处采样纹理值 f(x,y)f(x,y)
  • 图中黑点表示纹理采样位置

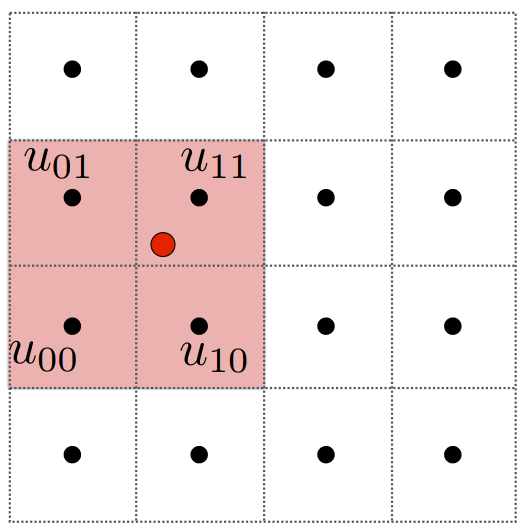
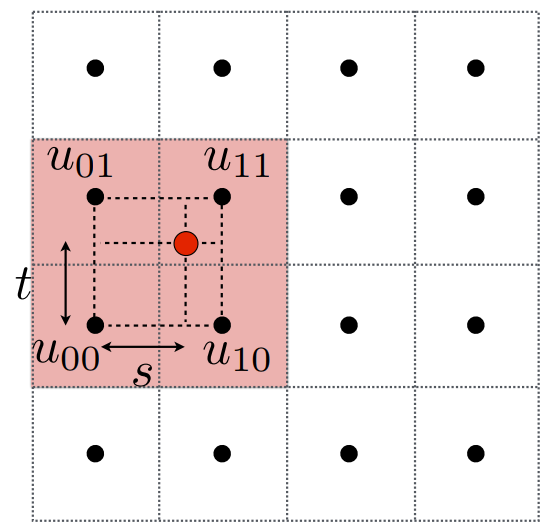
screenShot.png

  • 取4个最近的样本位置，并贴上纹理值。

screenShot.png

  • 分数偏移量 (s,t)(s,t) 如图所示，竖向为 tt ，横向为 ss ，均为 0 到 1 之间，两个 texel 之间间距为 1。

线性插值函数（1D）

lerp(x,v0,v1)=v0+x(v1−v0)lerp(x,v_0,v_1) = v_0 + x(v_1 - v_0)

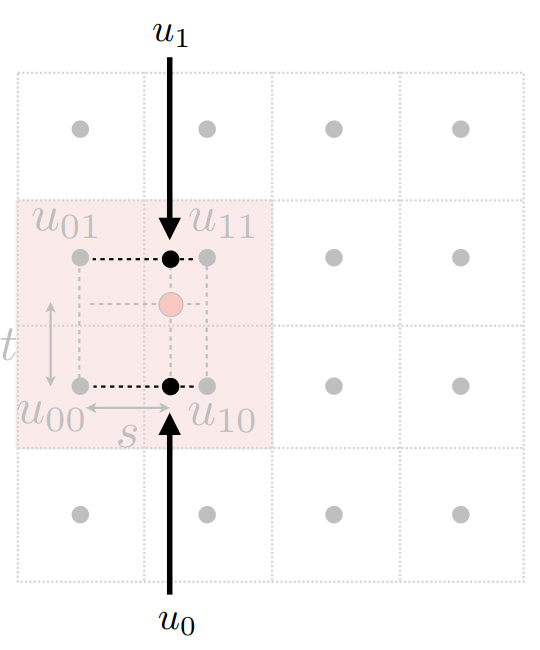
screenShot.png

使用两个辅助点进行插值（水平）：

u0=lerp(s,u00,u10)u1=lerp(s,u01,u11)\begin{aligned} &u_0 = lerp(s,u_{00},u_{10}) \\ &u_1 = lerp(s,u_{01},u_{11}) \end{aligned}

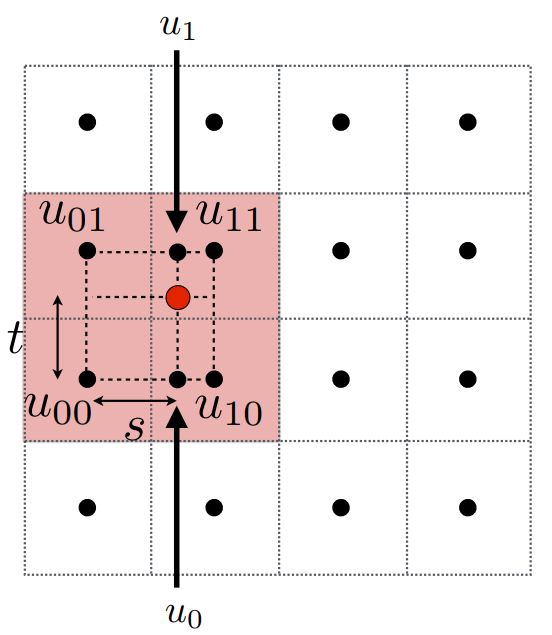
screenShot.png

最后再进行竖向插值，获得最终红点处的颜色结果：

f(x,y)=lerp(t,u0,u1)f(x,y) = lerp(t,u_0,u_1)

NOTE ：此时红点处的结果综合考虑了周围4个点的颜色。

3.2 双三次插值算法(bicubic interpolation)

参考文章：

4. 纹理过大

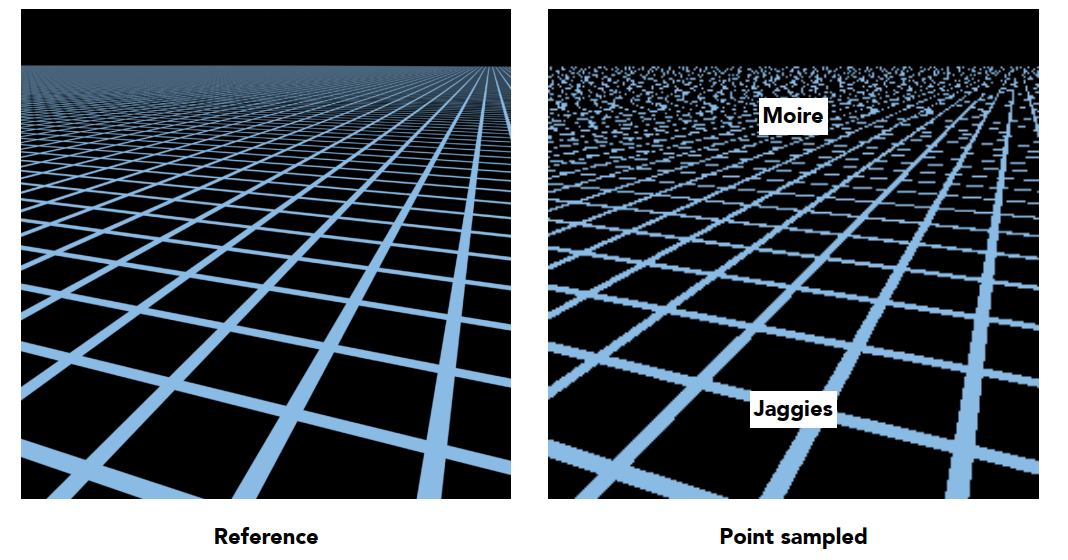
screenShot.png

远处产生摩尔纹，近处产生锯齿。

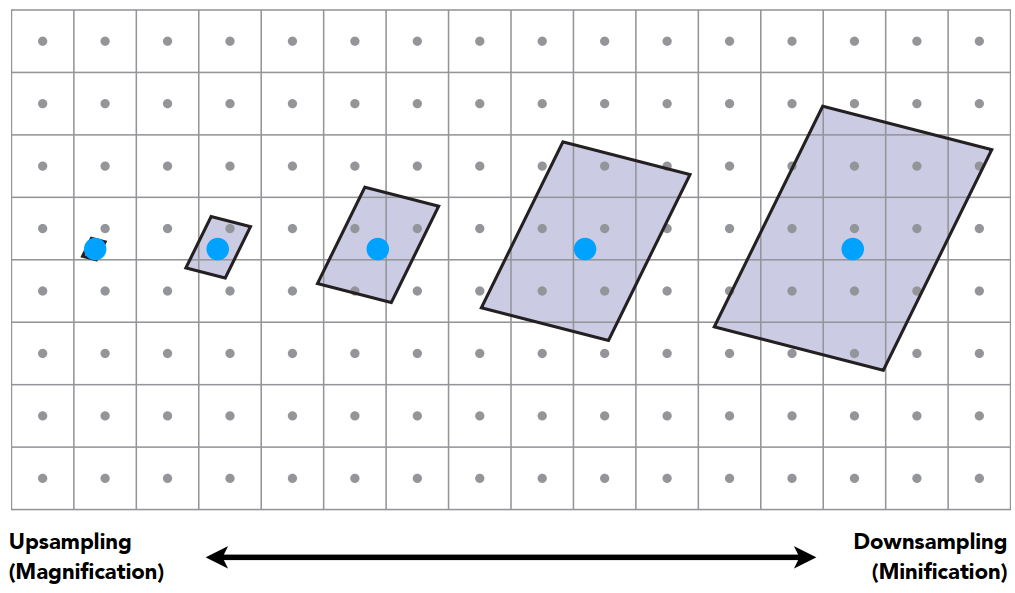
screenShot.png

  • 近处（左侧）单个像素覆盖的纹理区域相对较小。
  • 远处（右侧）单个像素覆盖的纹理区域相对较大，此时单个像素取区域内的所有纹理颜色的平均值。

单个像素内信号频率较高，此时仅用一个像素点进行采样，必然锯齿化。

4.1 点查询问题 vs 范围查询问题

Point Query vs. (Avg.) Range Query

点查询 ：采样以点为单位，计算单个点对应的值的大小。
范围查询 ：以范围为单位，直接计算该区域内部的平均值（有些范围查询也可能是计算最大值和最小值）。

4.2 Mipmap

Mipmap 允许（快速的、近似的、正方形区域的）范围查询。

screenShot.png

图中每层的分辨率依次缩小一半，存储量为原图的 43\cfrac{4}{3} 。

图像金字塔 ：

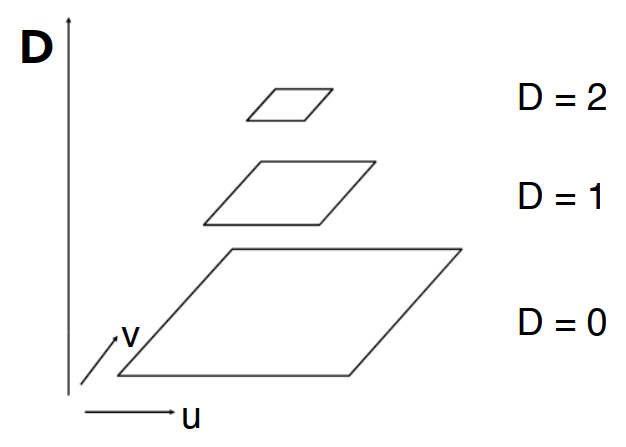
screenShot.png

计算 Mipmap 层级 D

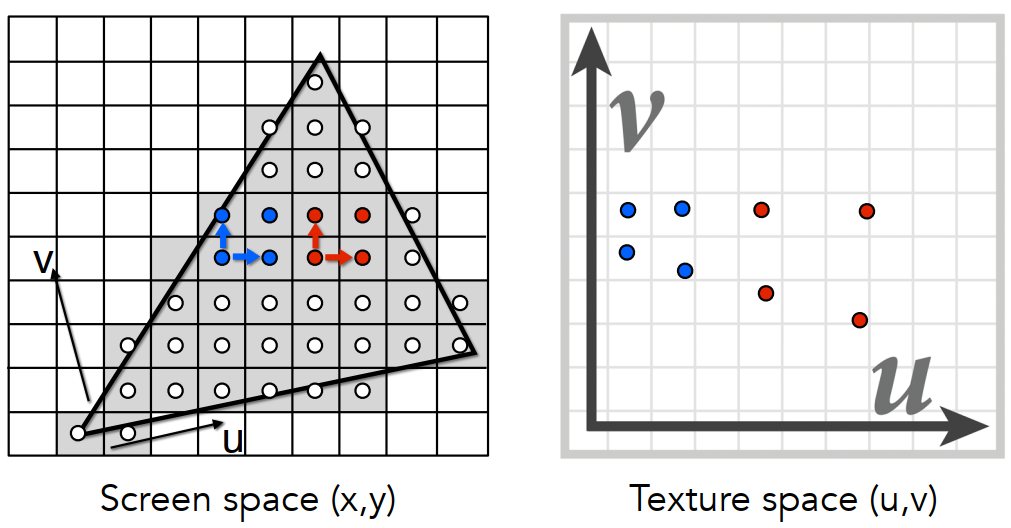
screenShot.png

使用相邻屏幕样本的纹理坐标估计纹理足迹。

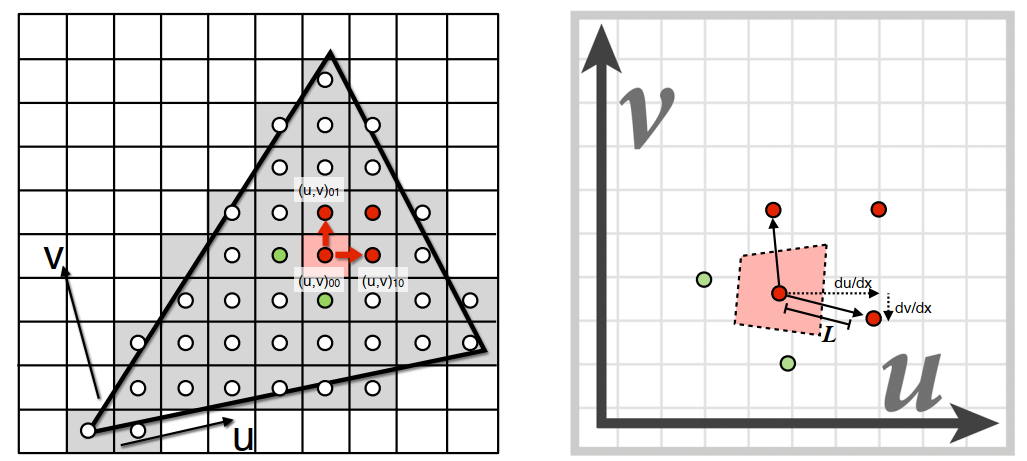
screenShot.png

例如：此时想计算图中红点的覆盖范围。
先计算自己的中心和相邻点的中心，分别投影到纹理图上。

D=log⁡2LL=max⁡((dudx)2+(dvdx)2,(dudy)2+(dvdy)2)\begin{aligned} &D = \log_2 L \\[2ex] &L = \max \left( \sqrt{\left(\cfrac{du}{dx}\right)^2 + \left(\cfrac{dv}{dx}\right)^2} , \sqrt{\left(\cfrac{du}{dy}\right)^2 + \left(\cfrac{dv}{dy}\right)^2} \right) \end{aligned}

计算像素空间上的间隔在纹理空间上对应间隔的微分。
此时计算长度 LL ，获得正方形框，近似计算出红色区域的面积。

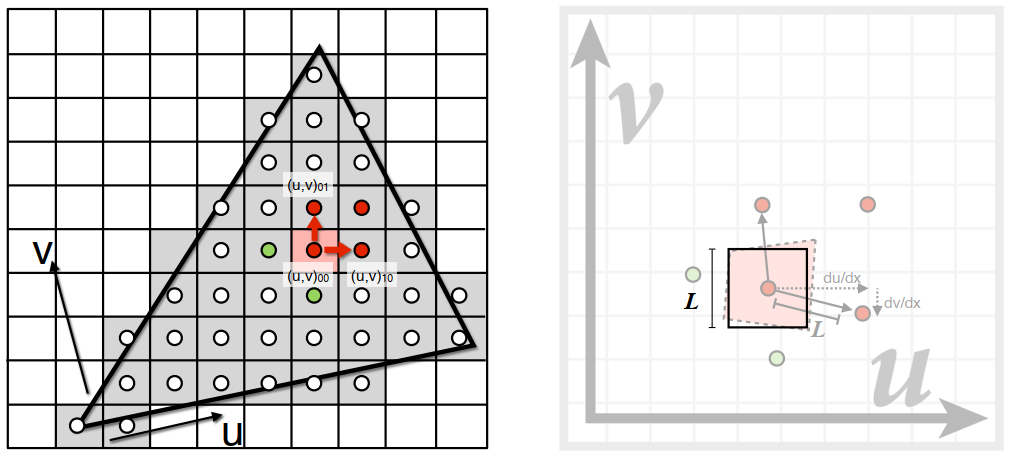
screenShot.png

  • 此时可以先计算该区域变成单个像素的层级数 D=log⁡2LD = \log_2 L ；
  • 然后再在对应层级进行查询。

screenShot.png

  • 如图所示，近处像素需要在低层级进行查询，远处像素需要在高层级进行查询。
  • 但因为层级是整数，结果是离散的结果，需要对每层进行插值。

4.2.1 三线性插值（Trilinear Interpolation）

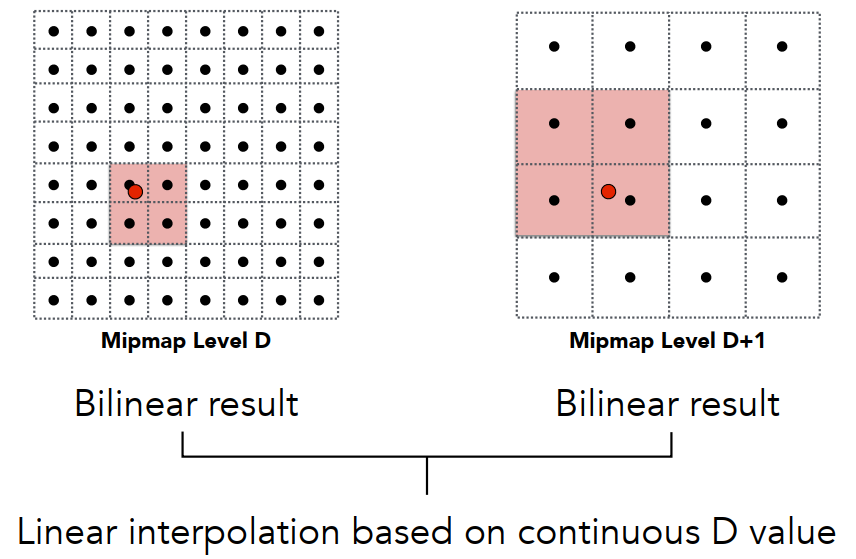
screenShot.png

  • 先对相邻两个层级分别进行双线性插值。
  • 再对其两个结果进行插值计算，整个过程即三线性插值。

screenShot.png

此时层级之间会进行一个过渡。

4.2.2 Mipmap 的局限性

过度模糊化：远处细节过于模糊。

screenShot.png

原屏幕空间中的图案映射到纹理空间后会出现不规则的形状。

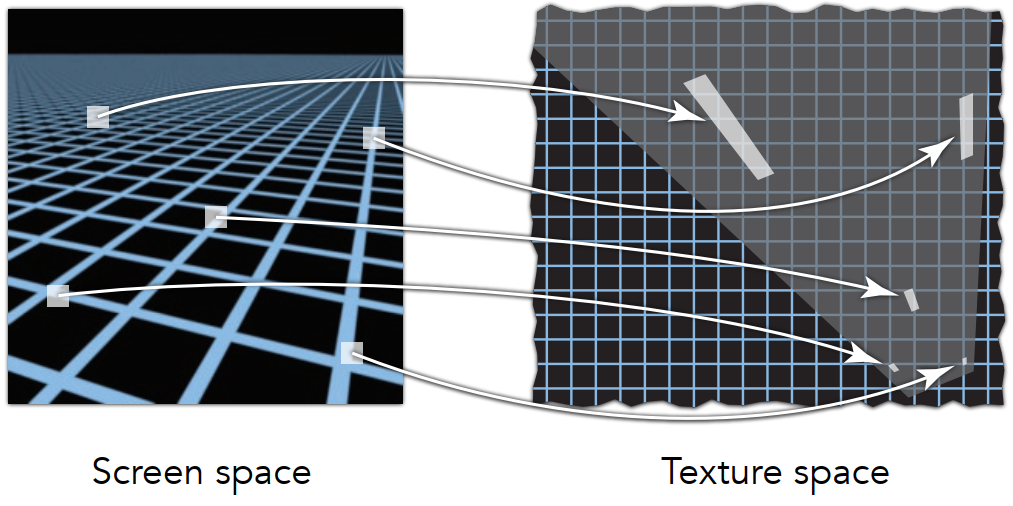
screenShot.png

4.2.3 各向异性过滤（Anisotropic Filtering）

screenShot.png

地形图和总面积表

screenShot.png

  • 可以查找 轴对齐的矩形区域 ；
  • 可见图中仅对竖直方向或者水平方向做了缩小，比起 Mipmap 多了不均匀的水平或者竖直方向的压缩图；
  • 允许对长条状的矩形区域进行查询；
  • 但对于斜向矩形区域，即对角线足迹的查询，仍然是一个问题。

NOTE ：

  • “各向异性2x” ：图中左上角 2×2 的区域；
  • “各向异性4x” ：图中左上角 4×4 的区域。
  • 原存储的3倍，显存足够的情况下，可以将各向异性开到最高，不影响其计算力。即不影响性能。

4.2.4 EWA 过滤

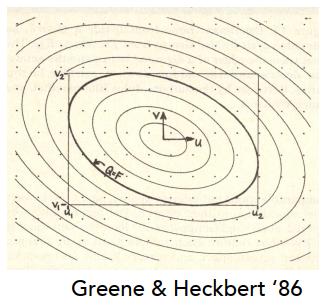
screenShot.png

  • 使用多个查找
  • 加权平均
  • Mipmap层次结构仍有帮助
  • 可以处理不规则的脚印