10 - 几何01_简介

1. 纹理的应用

在现代GPU中，

texture = memory + range query (filtering)

纹理 = 内存 + 在内存上的一个区域进行的范围查询（滤波）

• 将数据引入 片元（fragment） 计算的一般方法。

1.1 环境光照（Environment lighting）

将窗户的结构在 犹他茶壶（Utah Teapot） 上进行反射，可以用纹理进行描述。

此时有个假设：环境光来自无穷远，即在不同位置下的光源的方向和强度不变。

1.1.1 球型环境贴图（Spherical Environment Map）

用于渲染真实照明的环境贴图（Environment Map）（左）

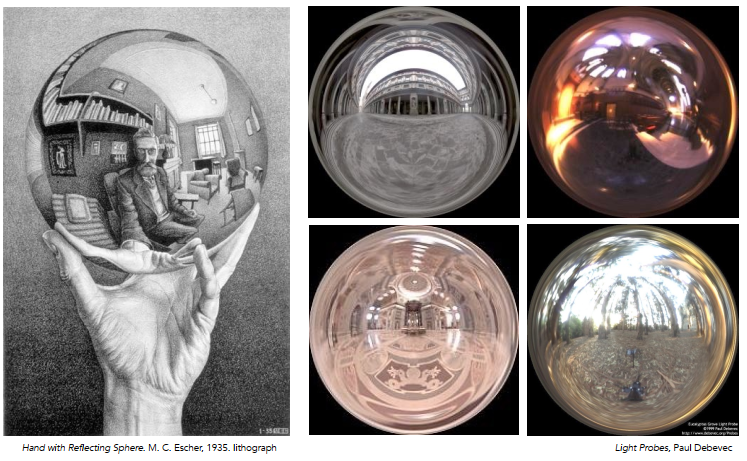
此时我们可以有一个逆向工程，将环境光信息记录在一个反射球体上。之后可以通过这个信息展开成周围实际的环境。这样我们就能通过这种方式来描述来自不同方向上的光照信息。

然而，当直接展开成周围环境时，会发生扭曲的现象。（顶部和底部部分会显得缩小）

解决方法 —— 立方体贴图（Cube Map）

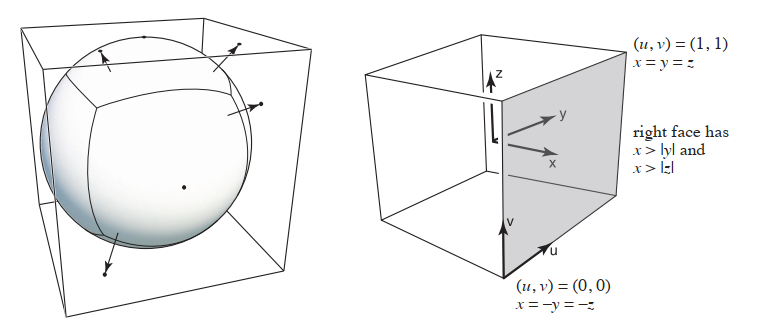
使用一个立方体包围盒将球体进行包围。将球面信息存储在一个立方体上。

展开后的实际效果。

1.2 体现几何表面的细节

1.2.1 凹凸贴图（Bump Mapping）

通过纹理定义某个点在基础表面上沿着法线方向的相对高度。

此时可以在不改变原始几何信息的情况下，仅仅通过应用一个复杂的纹理，模拟出复杂的几何表面形式。

通过不同的明暗对比，可以产生一个与之类似的着色结果，欺骗人眼。

1.2.1.1 凹凸贴图的原理

通过添加纹理而不改变几何信息

• 对每个像素的表面法线进行扰动。（仅仅对于着色计算）
• 纹理定义的每个点的“高度偏移（Height Shift）”
• 通过凹凸贴图修改对应的点的法向量。（图中 $\bold{p} \to \bold{n}$ ）

法线的计算过程 ：

2D 情况：

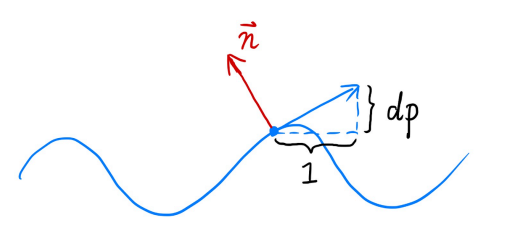
• 原始的表面法线，即在点 $p$ 的法线 $n(p) = (0, 1)$ ；
• $p$ 处的导数为 $dp = c * [h(p+1) - h(p)]$ ，其中的系数 $c$ 用来表示凹凸贴图的影响大小；
• 扰动法向为 $n(p) = (-dp, 1)$ ，之后进行归一化。

3D 情况：

• 原始曲面法线 $n(\bold{p}) = (0, 0, 1)$ ；
• p的导数（获得对应切线）
  $- d\bold{p}/d\bold{u} = c_1 * [h(\bold{u}+1) - h(\bold{u})]$
  $- d\bold{p}/d\bold{v} = c_2 * [h(\bold{v}+1) - h(\bold{v})]$
• 扰动法线为$n = (-d\bold{p}/d\bold{u}, -d\bold{p}/d\bold{v}, 1)$ ，注意归一化；
• 该处均是定义的该点的局部坐标系。

1.2.2 位移贴图（Displacement Mapping）

• 使用与凹凸贴图中相同的纹理；
• 但实际上又真的会对顶点进行相应的位移移动。

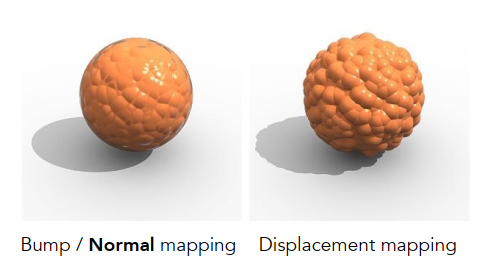
• 图中凹凸贴图的边缘是没有凹凸变化的；
• 位移贴图自身某个凸点的阴影会投射到相邻的其他凸点；
• 自然地，模型的几何信息会非常复杂，三角形的大小需要足够细致，才能足以表现该纹理。

1.3 3D空间噪声函数 + 实体建模

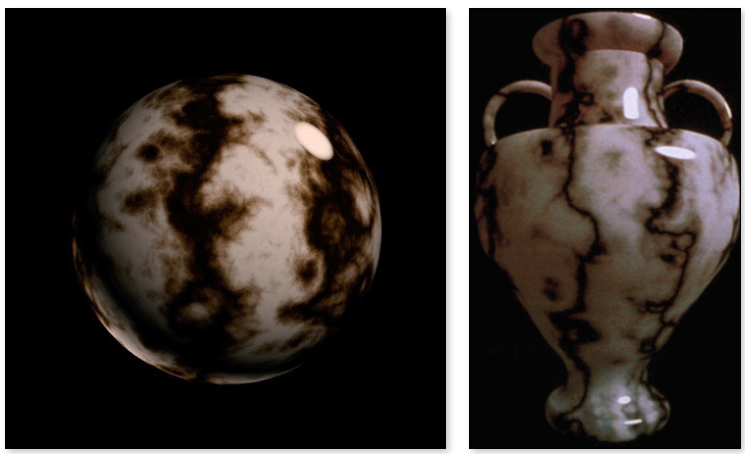
• 纹理不仅仅指2D的球面信息，有时候也可以是一个3D空间中的噪声信息；
• 此时可以表示3D空间中任何一个地方的信息。

1.4 存储预先计算的阴影信息

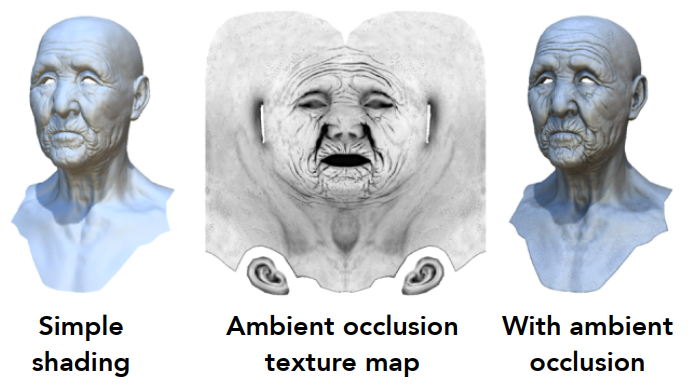
用纹理记录一些提前计算的信息。

1.5 使用3D纹理记录体积渲染

存储一些3D信息，常用于医学领域。

2. 几何（简介）

2.1 分类

隐式表示（Implicit）

• 代数曲面（algebraic surface）
• 水平集（level sets）
• 距离函数（distance functions）

显式表示（Explicit）

• 点云（point cloud）
• 多边形网格（polygon mesh）
• 细分，NURBS

2.1.1 隐式表示（Implicit）

基于点集的分类

• 不会表示实际每个点的信息，但是会表示满足某种特定关系的点集。

例如 ：

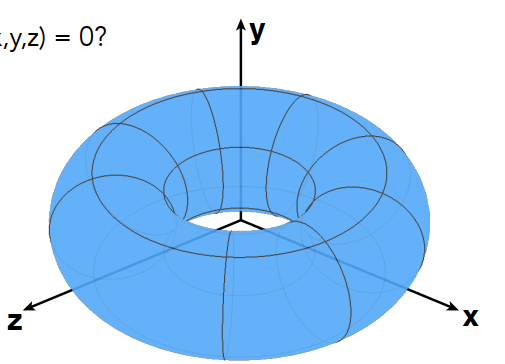
• 球面：三维中的所有点，其中 $x^2 + y^2 + z^2 = 1$ ；
• 更一般地，$f(x，y，z) = 0$ 。

隐式表示的特点：

• 很难直接通过隐式表示看出实际的图形，需要进行采样；
• 很容易检测某点是否在该图形上。

$f(x,y,z) = (2 - \sqrt{x^2 + y^2})^2 + z^2 - 1$

2.1.2 显式表示（Explicit）

• 所有点的信息都直接给出；
• 通过参数映射的方式给出。

$g:\Bbb{R}^2 \to \Bbb{R}^3;(u,v) \mapsto (x,y,z)$

$g(u,v) = f((2+\cos{u})\cos{v},(2+\cos{u})\sin{v},\sin{u})$

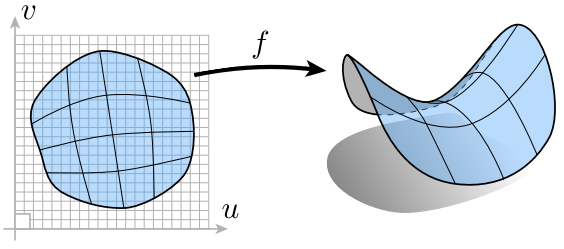
显式表示的特点：

• 很容易直接通过隐式表示看出实际的图形，需要进行采样；
• 很难检测某点是否在该图形上。

2.2 应用

2.2.1 CSG（Constructive Solid Geometry）（Implicit）

通过对几种基础几何体进行布尔运算，组合出更复杂的几何体。（几何是隐式表示）

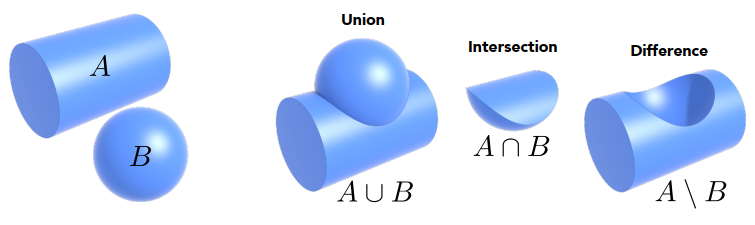
布尔表达式：

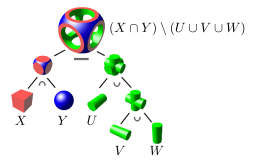
2.2.2 距离函数（Distance Functions）（Implicit）

代替布尔运算，使用 距离函数（Distance Functions） 将曲面逐渐融合在一起：

距离函数（Distance Functions） ：指的是空间中的任何一个点与待表述的几何形体上任意一点之间的最小距离，可以是 有符号距离（signed distance） 。

NOTE:

• 距离函数的值为零的位置为物体的边界。

上图中，获得两个物体的距离函数，对距离函数进行融合，之后再恢复成物体，即获得两个物体融合（Blending）后的物体。

示例 ：

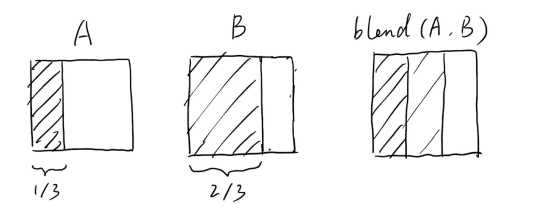
想获得由 A 到 B 运动的中间状态，但在简单的融合之后，实际出现 1/3 黑 1/3 灰 1/3 白，而理论上应该是 1/2 黑 1/2 白。

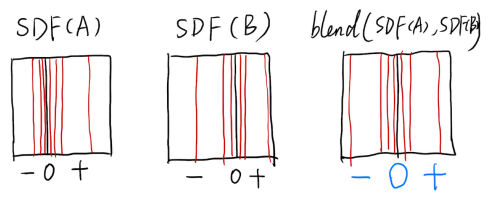
此时可以先分别求出 A 和 B 的有符号距离函数，然后再对距离函数进行融合，最后恢复成原图案。

2.2.3 水平集方法（Level Set Methods）（Implicit）

有些时候封闭形式的方程很难描述某些复杂的形状，这时很难求出对应的距离函数；

替代方法：存储一个近似函数的值网格。

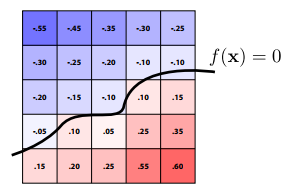
在插值等于零的地方找到曲面对形状提供更明确的控制（如纹理）。

2.2.4 分形（Fractals）（Implicit）

在所有尺度上表现出 自相似性 和细节，类似于递归。