04 - 视图变换

1. MVP 变换简介

• Model Transformation (placing objects)
  世界坐标系下有很多 Object ，用一个变化矩阵把它们的顶点坐标从Local坐标系（相对坐标）转换到世界Global坐标系（绝对坐标），这就是 模型变换 。
   
• View Transformation (placing camera)
  我们看到的画面由 camera 捕捉， camera 参数决定了我们在屏幕上看到的东西，这一步可以将世界坐标系转换到摄像机坐标系，这就是 视图变换 。
   
• Projection Transformation
  模型 / 视图变换之后，做一个投影变换，将三维空间中的物体投影到二维空间中。

2. 视图/相机变换（View/Camera Transformation）

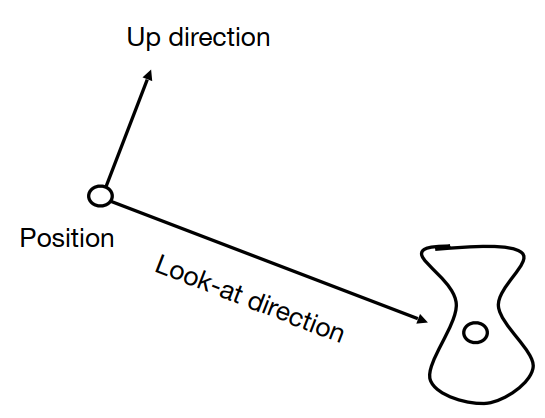
定义一个相机

• 位置（Position）： $\vec{e}$
• 朝向（Look-at/gaze direction）： $\hat{g}$
• 上方向（Up direction）： $\hat{t}$

关键 ：

• 若相机和所有的对象均一起发生移动，投影出来的 Photo 不会发生变化。

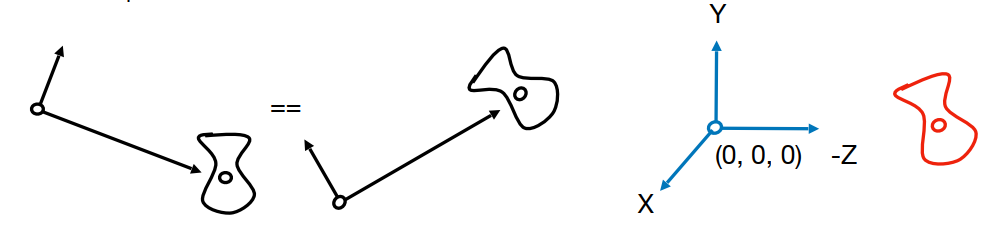
因此，我们总将 Camera 固定在一个 标准位置 ：

• 原点，Up direction 沿着 $y$ 轴方向，Look-at direction 沿着 $-z$ 轴；
• Camera 固定，让其他的对象跟随一起运动。

2.1 视图/相机变换

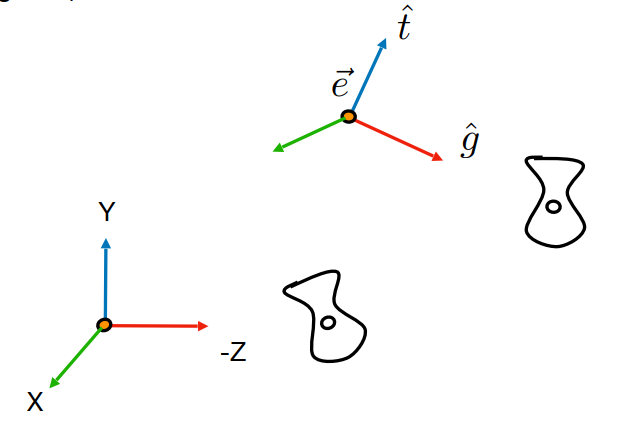
将相机从一个任意位置变换到标准位置

• 使用矩阵 $M_{view}$
  • 将其固定在原点，Up direction 沿着 $y$ 轴方向，Look-at direction 沿着 $-z$ 轴。
     
• 矩阵 $M_{view}$ 的数学性质：
  • 变换 $e$ 到原点；
  • 旋转 $g$ 到 $-z$ 轴；
  • 旋转 $(g \times t)$ 到 $x$ 轴。

构造矩阵 $M_{view}$ ：

• $M_{view} = R_{view}T_{view}$
• 将 $e$ 变换到原点的位移变换：

$T_{view} = \begin{bmatrix} 1 & 0 & 0 & -x_e \\ 0 & 1 & 0 & -y_e \\ 0 & 0 & 1 & -z_e \\ 0 & 0 & 0 & 1 \end{bmatrix}$

• 旋转矩阵 $g \mapsto -Z$ ， $t \mapsto Y$ ，$(g \times t) \mapsto X$
  不妨先求逆变换矩阵 $X \mapsto (g \times t)$ ， $Y \mapsto t$ ，$Z \mapsto -g$

$\begin{aligned} &R_{view}^{-1} = \begin{bmatrix} x_{\hat{g}\times\hat{t}} & x_t & x_{-g} & 0 \\ y_{\hat{g}\times\hat{t}} & y_t & y_{-g} & 0 \\ z_{\hat{g}\times\hat{t}} & z_t & z_{-g} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \\[8ex] &R_{view} = \begin{bmatrix} x_{\hat{g}\times\hat{t}} & y_{\hat{g}\times\hat{t}} & z_{\hat{g}\times\hat{t}} & 0 \\ x_t & y_t & z_t & 0 \\ x_{-g} & y_{-g} & z_{-g} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \end{aligned}$

NOTE ：

• 视图变换 变换的是 Camera ，其他的 Object 相对于 Camera 在进行移动；
• 若先进行了 模型变换 ，在后面进行 视图变换 时，会在移动 Camera 的同时，需要将 Object 也跟着 Camera 一同移动，以此保持 Photo 不变；
• 可见不管是 视图变换 还是 模型变换 ，最终本质上还是作用在 Object 上面，因此人们往往习惯将二者统称为 模型/视图变换（Model/View Transformation） 。

3. 投影变换（Projection transformation）

计算机图形学中的投影：

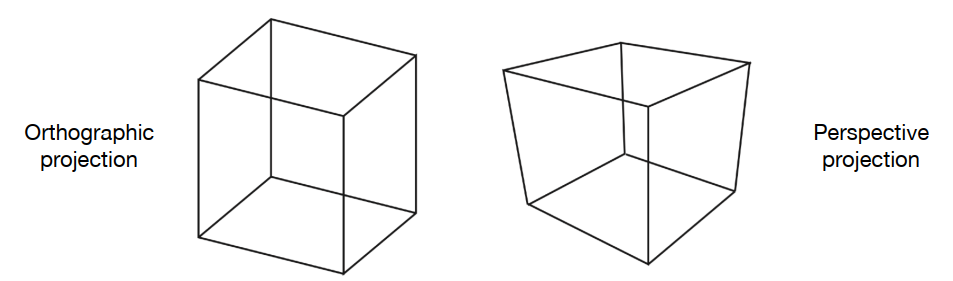
• 3D 到 2D
• 正交投影（Orthographic projection）
• 透视投影（Perspective projection）：会存在 “近大远小” 的现象

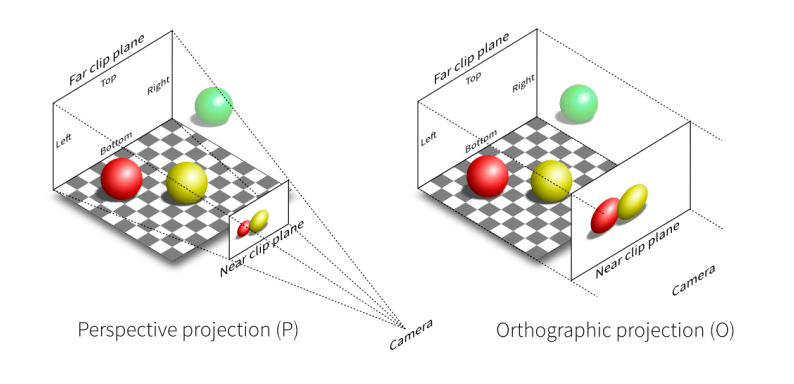
• 正交投影（Orthographic projection）：Camera 在一个 “点” 进行观察
• 透视投影（Perspective projection）：Camera 在 “无限远” 处进行观察

3.1 正交投影（Orthographic projection）

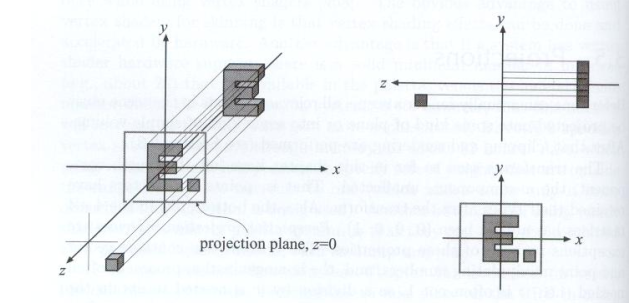
方法一 ：

• Camera 放置在原点，朝向 $-z$ 轴，上方向为 $y$ 轴；
• 消除掉 $z$ 轴上的信息；
• 将生成的矩形平移缩放至小矩形 $[-1,1]^2$ 上。

方法二 ：

• 先通过 6 个参数描述一个立方体（AABB）；
• 将其映射到正则立方体（“Canonical” Cube）：

$[l,r]\times[b,t]\times[\bold{f},\bold{n}] \mapsto [-1,1]^3$

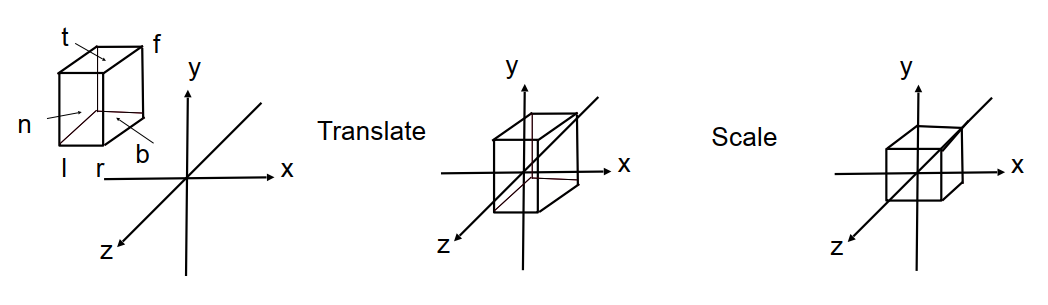
NOTE ：

• 先将中心平移到原点，之后再将轴缩放到 $[-1,1]^3$
• 因为 Camera 是沿着 $-z$ 轴的方向（右手坐标系），因此远的地方 $z$ 值较小，近的地方 $z$ 值较大

构造矩阵 $M_{ortho}$ ：

• 先将中心点平移至原点：

$T_{ortho} = \begin{bmatrix} 1 & 0 & 0 & -\frac{r+l}{2} \\[1.5ex] 0 & 1 & 0 & -\frac{t+b}{2} \\[1.5ex] 0 & 0 & 1 & -\frac{n+f}{2} \\[1.5ex] 0 & 0 & 0 & 1 \end{bmatrix}$

• 将 length/width/height 缩放至 2

$R_{ortho} = \begin{bmatrix} \frac{2}{r-l} & 0 & 0 & 0 \\[1.5ex] 0 & \frac{2}{t-b} & 0 & 0 \\[1.5ex] 0 & 0 & \frac{2}{n-f} & 0 \\[1.5ex] 0 & 0 & 0 & 1 \end{bmatrix}$

• 可得最后的正交投影矩阵为：

$M_{ortho} = R_{ortho} \cdot T_{ortho} = \begin{bmatrix} \frac{2}{r-l} & 0 & 0 & 0 \\[1.5ex] 0 & \frac{2}{t-b} & 0 & 0 \\[1.5ex] 0 & 0 & \frac{2}{n-f} & 0 \\[1.5ex] 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & -\frac{r+l}{2} \\[1.5ex] 0 & 1 & 0 & -\frac{t+b}{2} \\[1.5ex] 0 & 0 & 1 & -\frac{n+f}{2} \\[1.5ex] 0 & 0 & 0 & 1 \end{bmatrix}$

3.2 透视投影（Perspective projection）

• 近大远小
• 平行线不再平行；会收敛到一个点

• 齐次坐标表示的点 $(x,y,z,1)$ 和 $(kx,ky,kz,k)$ 均表示三维空间中的点 $(x,y,z)$ ，其中 $k \neq 0$ ；
• 显然当 $k = z$ 时，可以用 $(xz,yz,z^2,z)$ 表示点 $(x,y,z)$ ，其中 $z \neq 0$ ；
• eg. ： $(1,0,0,1)$ 和 $(2,0,0,2)$ 都表示点 $(1,0,0)$

3.2.1 透视投影的过程

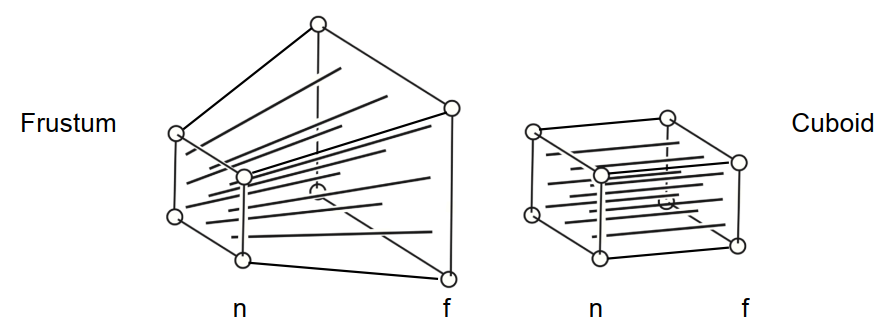
• 先将 Frustum 挤压成一个 Cuboid ：（ $n \to n$ ， $f \to f$ ， $M_{persp \to ortho}$ ）：
  • 挤压过程中 “近平面（near plane）”（ $z = n$ ） 不会发生变化；
  • 挤压过程中 “远平面（far plane）”（ $z = f$ ） 仅在 $xOy$ 平面上变化，$z$ 轴上的值不发生变化，特别地，中心点不会发生变化。
• 再做正交投影（使用 $M_{ortho}$ ）

3.2.2 构造变换矩阵

STEP - 01：先找到在 xoy 平面上的变换关系

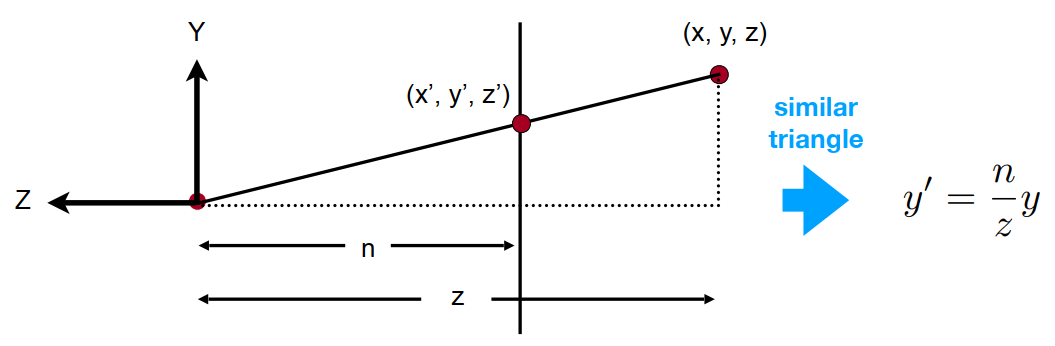
• 找起始点 $(x,y,z)$ 和变换后的点 $(x',y',z')$ 。
• 可以找到各个分量的对应关系：$x' = \cfrac{n}{z}x$ ，$y' = \cfrac{n}{z}y$
• 暂时可以获得以下关系：

$\begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} \xmapsto{M_{persp \to ortho}^{(4 \times 4)}} \begin{pmatrix} nx/z \\ ny/z \\ unknown \\ 1 \end{pmatrix} \xrightarrow{mult. \space by \space z} \begin{pmatrix} nx \\ ny \\ unknown \\ z \end{pmatrix}$

• 可以先构造 $M_{persp \to ortho}$ 的一部分：

$M_{persp \to ortho} = \begin{pmatrix} n & 0 & 0 & 0 \\[1.5ex] 0 & n & 0 & 0 \\[1.5ex] ? & ? & ? & ? \\[1.5ex] 0 & 0 & 1 & 0 \end{pmatrix}$

STEP - 02：再找在 z 轴方向上的变换关系

矩阵 $M_{persp \to ortho}$ 中的第三排控制 $z \mapsto z'$ ：

• “近平面（near plane）”（ $z = n$ ）上的任意点不会发生变化：

$\begin{pmatrix} x \\ y \\ n \\ 1 \end{pmatrix} \xmapsto{M_{persp \to ortho}^{(4 \times 4)}} \begin{pmatrix} x \\ y \\ n \\ 1 \end{pmatrix} \xrightarrow{mult. \space by \space n} \begin{pmatrix} nx \\[1.25ex] ny \\[1.25ex] n^2 \\[1.25ex] n \end{pmatrix}$

设矩阵的第三行为 $\begin{pmatrix} 0 & 0 & A & B\end{pmatrix}$ ，则有：

$\begin{pmatrix} 0 & 0 & A & B \end{pmatrix} \begin{pmatrix} x \\ y \\ n \\ 1 \end{pmatrix} = n^2$

可得表达式：$An + B = n^2$
 

• “远平面（far plane）”（ $z = f$ ）上的点的 $z$ 分量不会发生变化，不过这里我们只观察中心点 $(0,0,f)$ ，在经过挤压变换之后没有发生任何变化：

$\begin{pmatrix} 0 \\ 0 \\ f \\ 1 \end{pmatrix} \xmapsto{M_{persp \to ortho}^{(4 \times 4)}} \begin{pmatrix} 0 \\ 0 \\ f \\ 1 \end{pmatrix} \xrightarrow{mult. \space by \space n} \begin{pmatrix} 0 \\ 0 \\ f^2 \\ f \end{pmatrix}$

可得表达式：$Af + B = f^2$
 

• 可以解得矩阵第三行中待定的系数 $A$ 和 $B$ ：

$\begin{cases} An + B = n^2 \\ Af + B = f^2 \end{cases} \Rightarrow \begin{cases} A = n + f \\ B = -nf \end{cases}$

SETP - 03 ：构造透视投影矩阵

此时已经得到了 挤压矩阵 $M_{persp \to ortho}$ ：

$M_{persp \to ortho} = \begin{pmatrix} n & 0 & 0 & 0 \\[1.5ex] 0 & n & 0 & 0 \\[1.5ex] 0 & 0 & n + f & -nf \\[1.5ex] 0 & 0 & 1 & 0 \end{pmatrix}$

因此可得 透视投影矩阵 为：

$\begin{aligned} &M_{persp} = M_{ortho} \cdot M_{persp \to ortho} = \\[3ex] &\begin{bmatrix} \frac{2}{r-l} & 0 & 0 & 0 \\[1.5ex] 0 & \frac{2}{t-b} & 0 & 0 \\[1.5ex] 0 & 0 & \frac{2}{n-f} & 0 \\[1.5ex] 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & -\frac{r+l}{2} \\[1.5ex] 0 & 1 & 0 & -\frac{t+b}{2} \\[1.5ex] 0 & 0 & 1 & -\frac{n+f}{2} \\[1.5ex] 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} n & 0 & 0 & 0 \\[1.5ex] 0 & n & 0 & 0 \\[1.5ex] 0 & 0 & n + f & -nf \\[1.5ex] 0 & 0 & 1 & 0 \end{bmatrix} \end{aligned}$