1. 投影变换(Perspective Projection)
视锥中的概念:
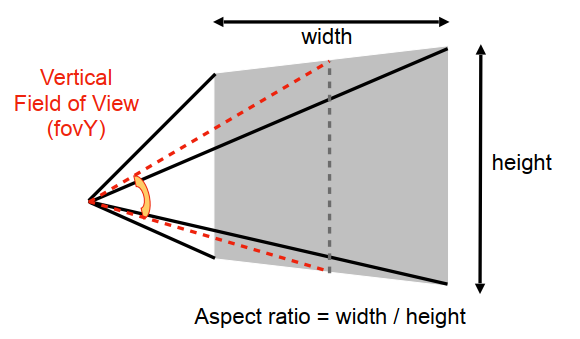
- 宽高比(Aspect ratio) :宽和高的比值;
- 垂直可视角 fovY(Vertical Field-of-View) :可见角度的范围,屏幕上下边中点与 Camera 点的两条连线的夹角。
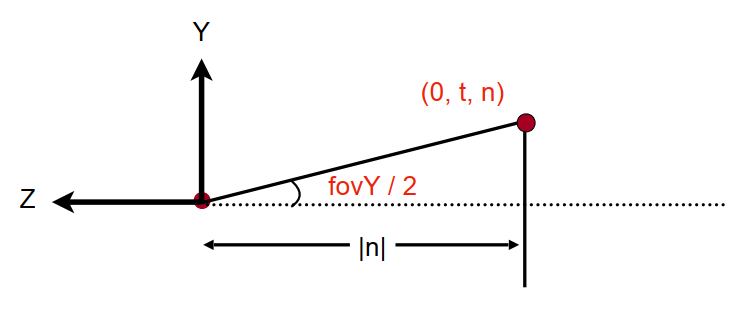
- tan2fovY=∣n∣t
- aspect=tr
在经过投影变换之后,所有 Object 均投影到 正则立方体(“canonical” cube) [−1,1]3
2. 屏幕(Sceen)
2.1 相关概念
- 像素的二维数组;
- 分辨率(Resolution) :屏幕的大小;
- 一种典型的光栅成像设备;
- 光栅化(Rasterize) :将 Object 绘制在屏幕上;
- 像素(Pixel) :是 “图片元素”(picture element) 的缩写;
- 像素是一个颜色均匀的正方形
- 颜色是(red, green, blue)的混合
2.2 屏幕的定义
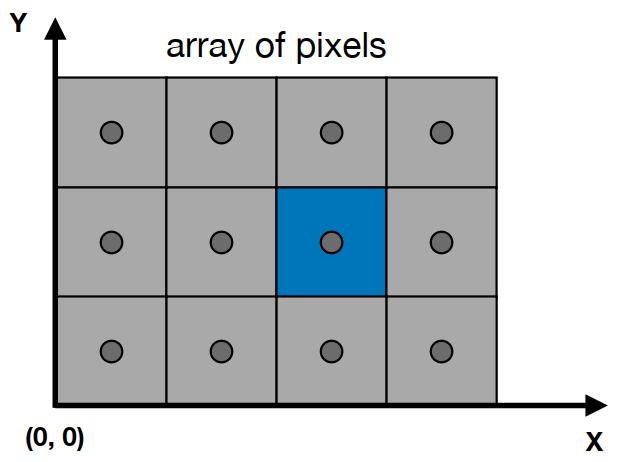
- 像素的坐标都可以表示成 (x,y) ,其中 x 和 y 都是整数;
- 设原点为 (0,0) ,那么所有像素都可以表示成 (0,0)→(width−1,height−1) ;
- 像素 (x,y) 的中心为 (x+0.5,y+0.5) ;
- 屏幕覆盖的范围: (0,0)→(width,height) 。
2.3 正则立方体到屏幕
- 与 z 轴分量无关;
- 仅在 xOy 平面上进行变换:[−1,1]2↦[0,width]×[0,height]
视口变换矩阵(Viewport transform matrix) :
Mviewport=⎝⎜⎜⎜⎜⎜⎛2width00002height0000102width2height01⎠⎟⎟⎟⎟⎟⎞
- 将正则立方体的宽度和高度缩放至 width 和 height ;
- 将正则立方体的中心位移至屏幕的中心点 (2width,2height) ;
- z 方向上不发生变化。
3. 光栅化
绘制到光栅成像设备:
- 多边形网格(Polygon Meshes)
- 三角形网格(Triangle Meshes)
3.1 使用三角形的原因
- 三角形是最基础的多边形;
- 任何多边形都能被剖分成若干个三角形;
- 保证是平面的,而四边形有可能 4 个点不在同一个平面上;
- 轮廓定义明确,不存在凹凸的性质,可以用叉积判断某点与三角形的碰撞情况;
- 三角形上的顶点的插值方法定义明确(重心插值)。
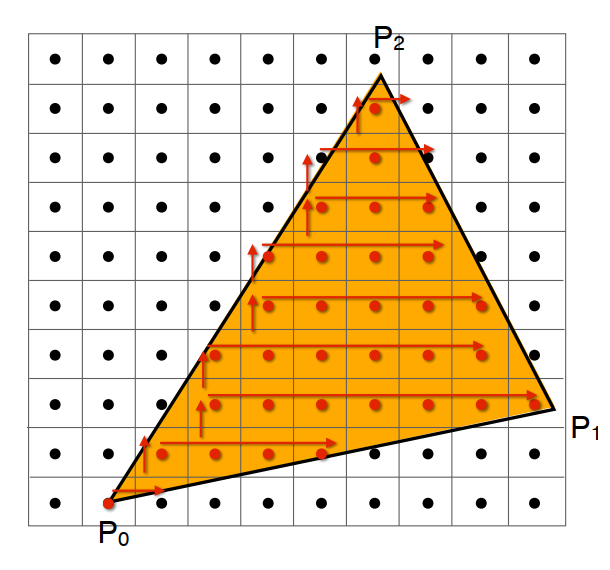
3.2 将三角形像素化
判断像素的中心点与三角形的位置关系
3.2.1 采样法
- 通过若干个点上计算一个函数就是 采样(sampling) ;
- 采样(sampling) 就是将函数 离散化(discretize) 。
1
2
| for (int x = 0; x < xmax; ++x)
output[x] = f(x);
|
这里我们利用 “像素的中心” 对屏幕空间进行采样,将屏幕离散化;
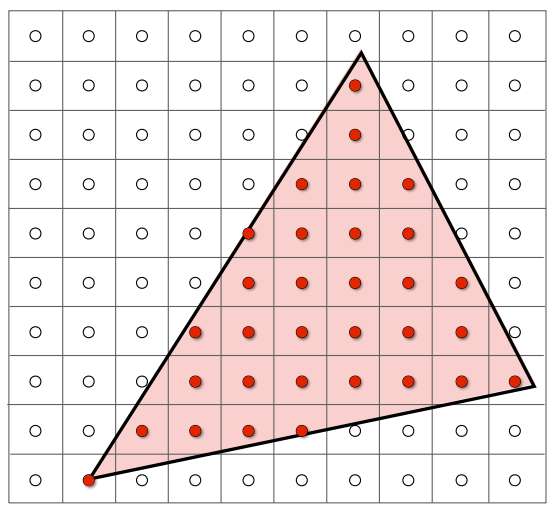
定义一个函数,判断像素的中心是否在三角形内:
inside(t,x,y)=⎩⎨⎧1 Point(x,y) in triangle t0 otherwise
在二维空间用指示器函数进行采样:
1
2
3
| for (int x = 0; x < xmax; ++x)
for (int y = 0; y < ymax; ++y)
image[x][y] = inside(tri, x + 0.5, y + 0.5);
|

判断点是否在三角形内 :
- 使用叉积判断左右关系;
- 具体参考 《01 - 数据结构定义》 4.3.2 public boolean pointInside(Point p):
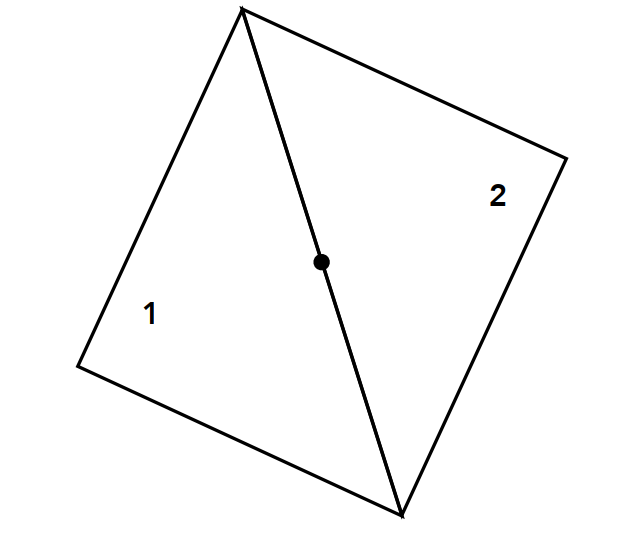
边界处理 :
- 上边和左边:算在三角形上;
- 下边和右边:不算在三角形上。
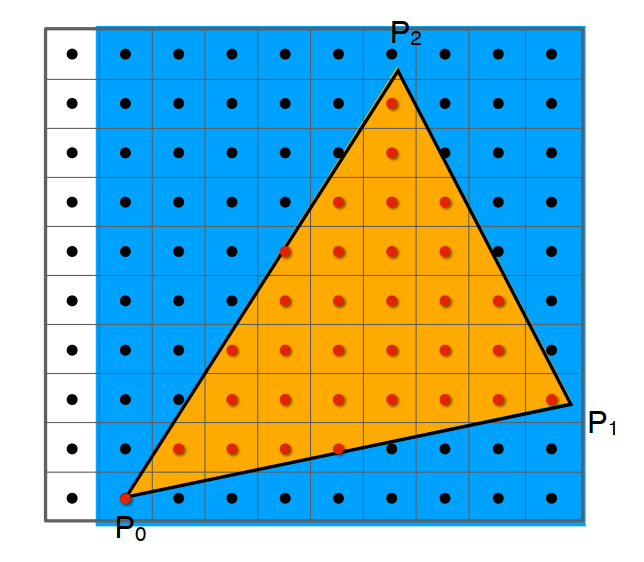
三角形的轴向包围盒 AABB :
特殊的加速方法 :