06 - 光栅化_抗锯齿和Z缓冲

1. 走样（Aliasing）

1.1 采样理论

在像素中心测试输入 / 输出 $\triangle$ 值

实际渲染出来的三角形：像素是均匀着色的正方形，出现锯齿

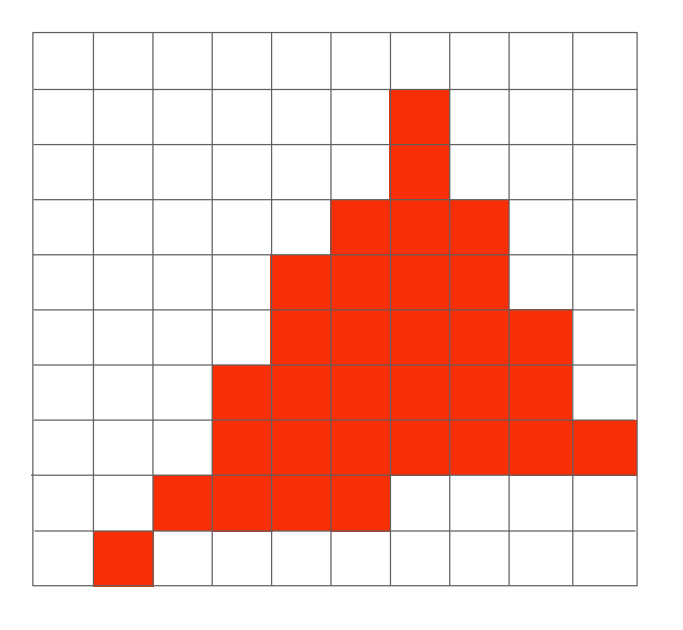
期望的三角形：连续三角函数

1.2 采样瑕疵（Sampling Artifacts）

• 这是 锯齿（aliasing） 的一个例子

• 成像中出现的 莫尔纹（Moiré Patterns）
  产生原因：渲染时跳过奇数行和列

• 车轮错觉（假动作） ：车轮旋转速度过快时会感觉车轮在倒着旋转
  产生原因：人眼在时间中的采样跟不上车轮旋转的速度

在 锯齿瑕疵（Aliasing Artifacts） 背后的本质问题：

• 信号变化过快（高频）
• 采样速度过慢

1.3 抗锯齿

基本思想 ：在采样之前进行 模糊（Blurring）/ 预过滤（Pre-Filtering）

由于单个像素值只能设置为红色或者白色，导致会出现栅格化三角形中的锯齿状物

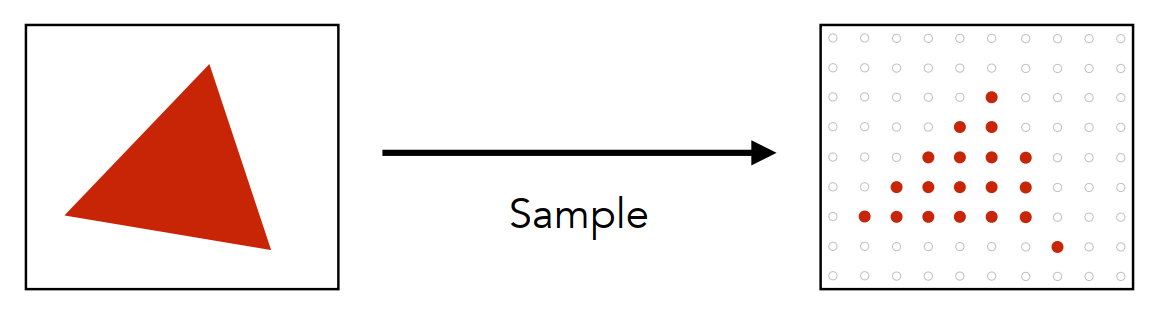
可以先对三角形进行模糊操作，使得单个像素值能设置为红色与白色之间的中间插值

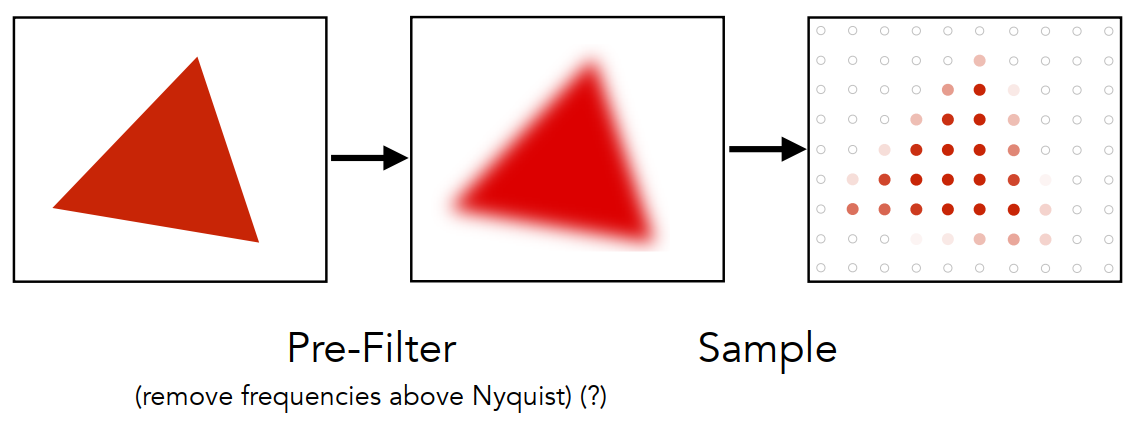
1.4 实践中的抗锯齿

抗锯齿（Antialiasing） 与 模糊锯齿（Blurred Aliasing）

• 左边 ：先采样后过滤，出现错误
• 右边 ：先过滤后取样

2. 频域（Frequency Domain）

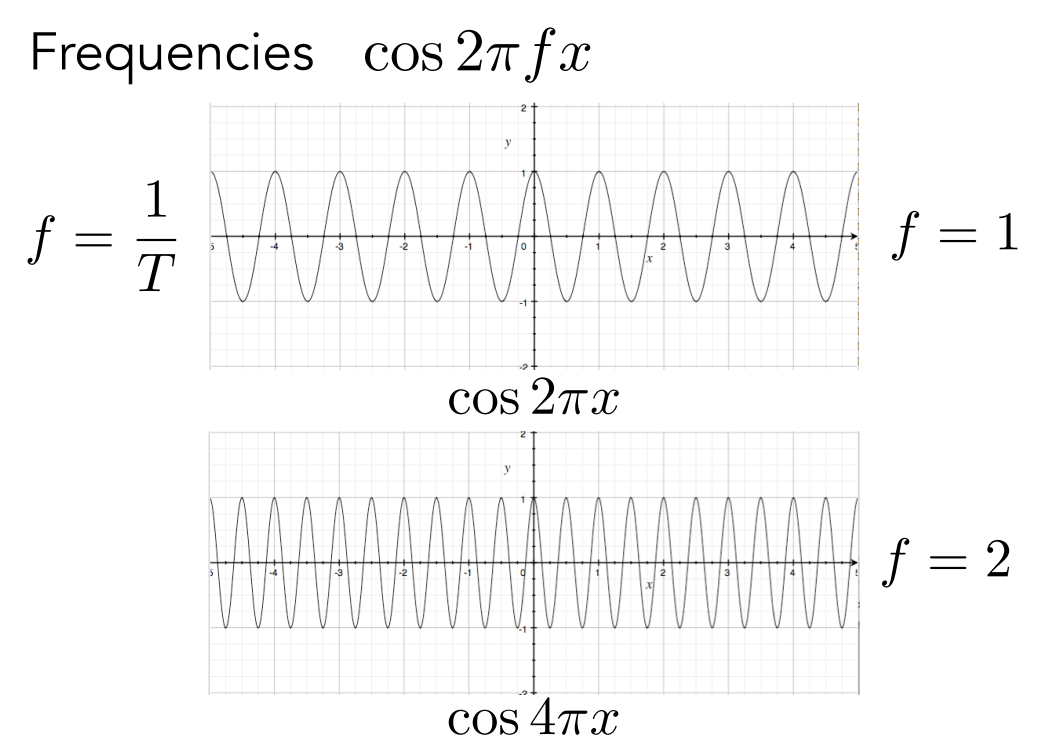
可以通过设置为 $f$ 的值去定义余弦波变换的快慢

3. 傅里叶变换（Fourier Transform）

3.1 傅里叶级数展开

• 任何周期函数都能表示为正弦和余弦的线性组合
• 可以通过傅里叶级数展开将函数分解成不同频率的余弦值

$f(x) = \frac{A}{2} + \frac{2A \cos{(t \omega)}}{\pi} - \frac{2A \cos{(3t \omega)}}{3 \pi} + \frac{2A \cos{(5t \omega)}}{5 \pi} - \frac{2A \cos{(7t \omega)}}{7 \pi} + \cdots$

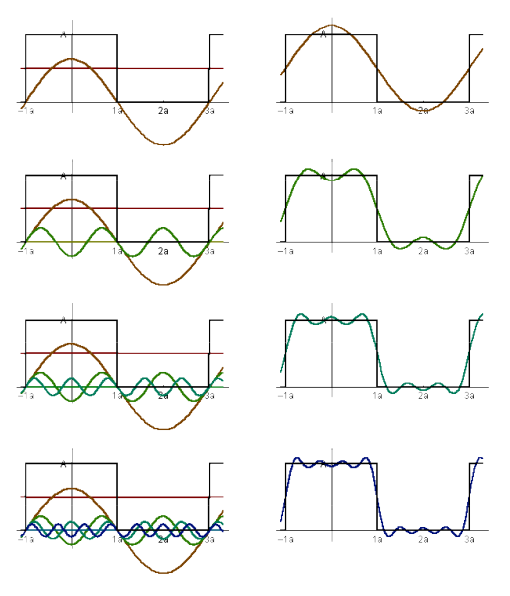
NOTE ：上式中的每一项对应图中的每一行

3.2 傅里叶变换（Fourier Transform）

$f(x) \xmapsto{Fourier \space Transform} F(\omega)$

傅里叶变换（Fourier Transform） ：$F(\omega) = \int_{- \infty}^{\infty}{f(x)e^{-2\pi i\omega x}dx}$

 

$F(\omega) \xmapsto{Inverse \space Transform} f(x)$

逆傅里叶变换（Inverse Transform） ：$f(x) = \int_{- \infty}^{\infty}{F(\omega)e^{2\pi i\omega x}d\omega}$

Recall ：$e^{ix} = \cos{x} + i \sin{x}$

4. 采样速度

更高的频率需要快速采样

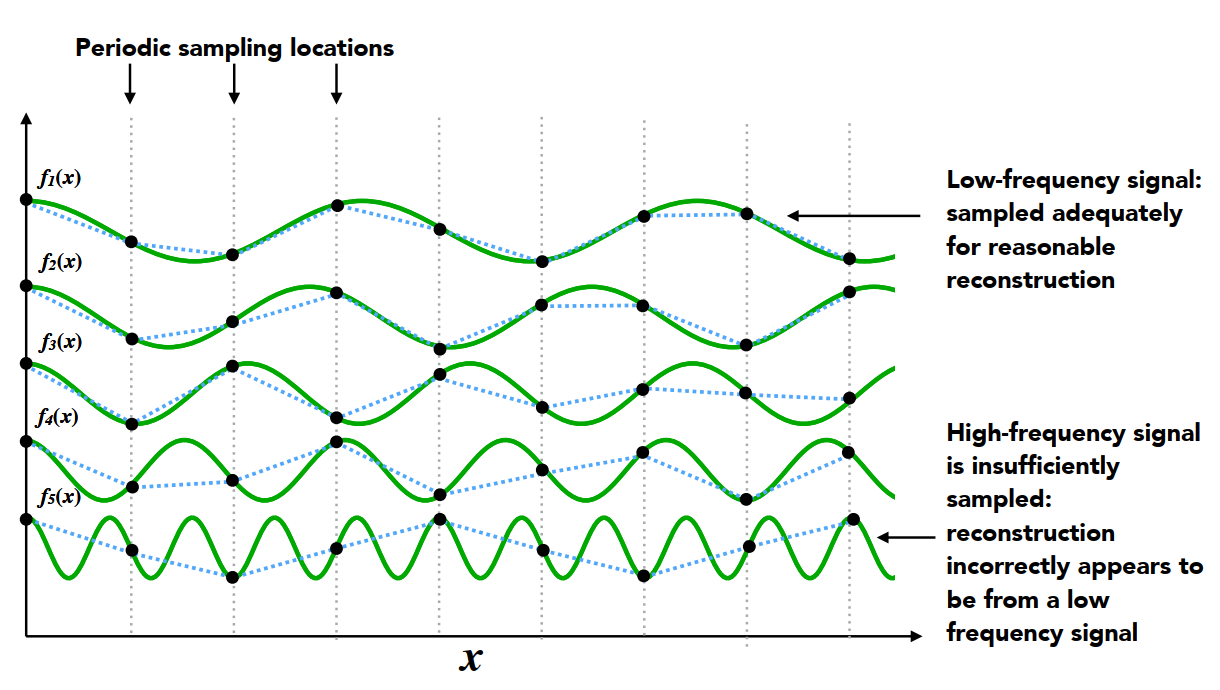
• 低频信号（Low-frequency signal） ：采样充分，可以很好的恢复出原函数
• 高频信号（High-frequency signal） ：此时采样点不够充足，此时难以恢复出原函数：最后可能会恢复成一个错误的低频信号

欠采样（Undersampling） 会产生 频率走样（Frequency Aliases）

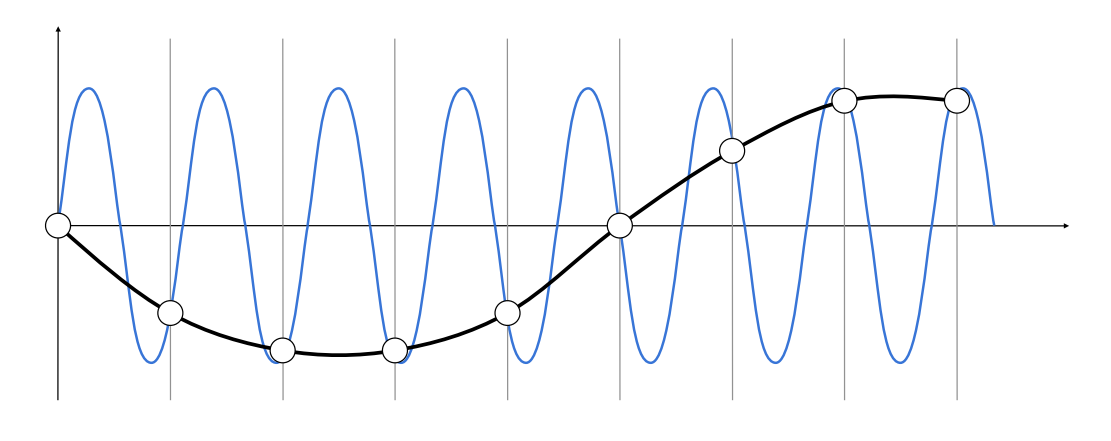
NOTE ：

• 图中蓝色图像是原函数，黑色图像是恢复出来的函数
• 显然，当用某个采样速度同时去采样一个高频信号（蓝色）和一个低频信号（黑色）时，可能最后都会恢复成一个低频信号（黑色）

5. 滤波（Filtering）

滤波（Filtering） ：移除特定的 频率成分（frequency contents）

傅里叶变换的作用 ：将函数从 时域（spatial domain） 变换为 频域（frequency domain） （从图像空间变换为频率空间）

NOTE ：

• 右图中，中心为低频区域，周围为高频区域。
• 显然，主要信息都集中在低频信息里。
• 右图中的十字型纹理 ：
  • 对于一个信号，我们往往将其看成一个周期性重复的信号；
  • 而当信号不是周期性重复的时候（例如图中示例），这种情况下会将该图像处理成 一个周期性信号中的一个周期 ，这会导致边界具有连续性，即左边界可以与右边界相连，上边界可以与下边界相连；
  • 当强行将左边界可以与右边界相连时，两个边界之间会发生剧烈的信号变换，这会产生一个信息较多的低频信息区域

5.1 高通滤波（High-pass filter）

消除低频信号，只保留高频，通过逆傅里叶变换获得图像，会发现高频信号有意义，表示的是 图像的边界 。

图像的边界 ：图像中的信息发生突变的位置，显然该处会出现高频信息

5.2 低通滤波（Low-pass filter）

消除高频信号，只保留低频，通过逆傅里叶变换获得图像， 图像的边界 会被渐渐消除，得到一张模糊图像。

5.3 滤除高频信息和低频信息

消除高频信号和低频信号，只保留中间某一段的信号，通过逆傅里叶变换获得图像，提取到一些不是很明显的 图像的边界 。

当将截取的圈扩大时

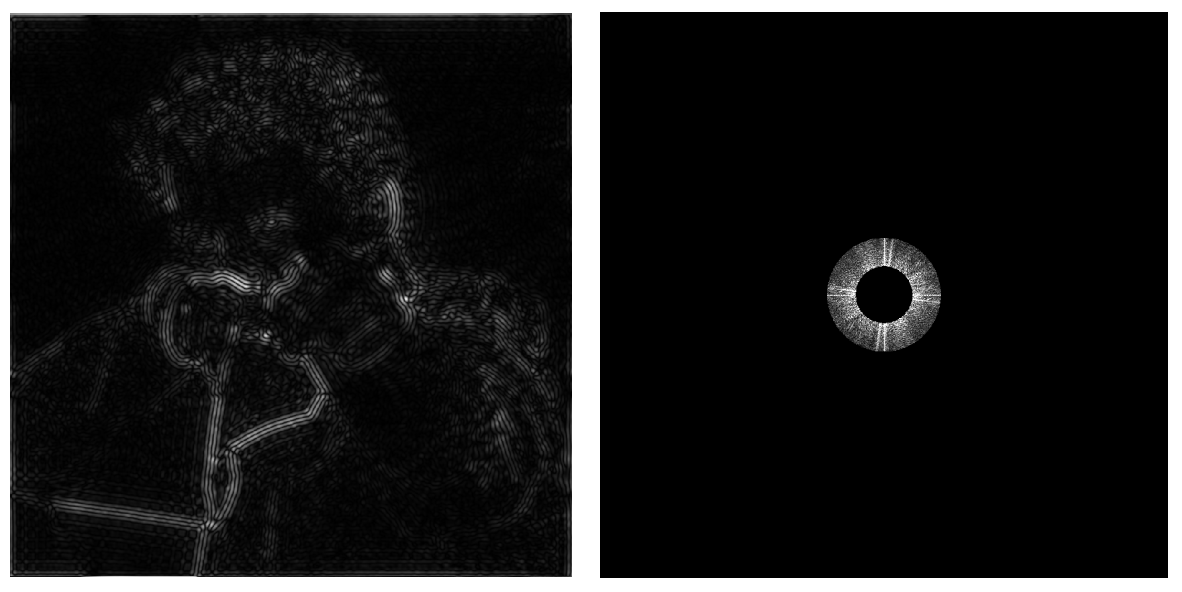
显然由于截取的范围在靠近周围的高频信号区域，通过逆傅里叶变换获得图像中， 图像的边界 会逐渐清晰，趋向于高频边界。

5.4 另一种滤波方式 —— 卷积

滤波是一种卷积

滤波（Filtering） = 卷积（Convolution） = 平均值（Averaging）

• 模糊就是一种平均操作

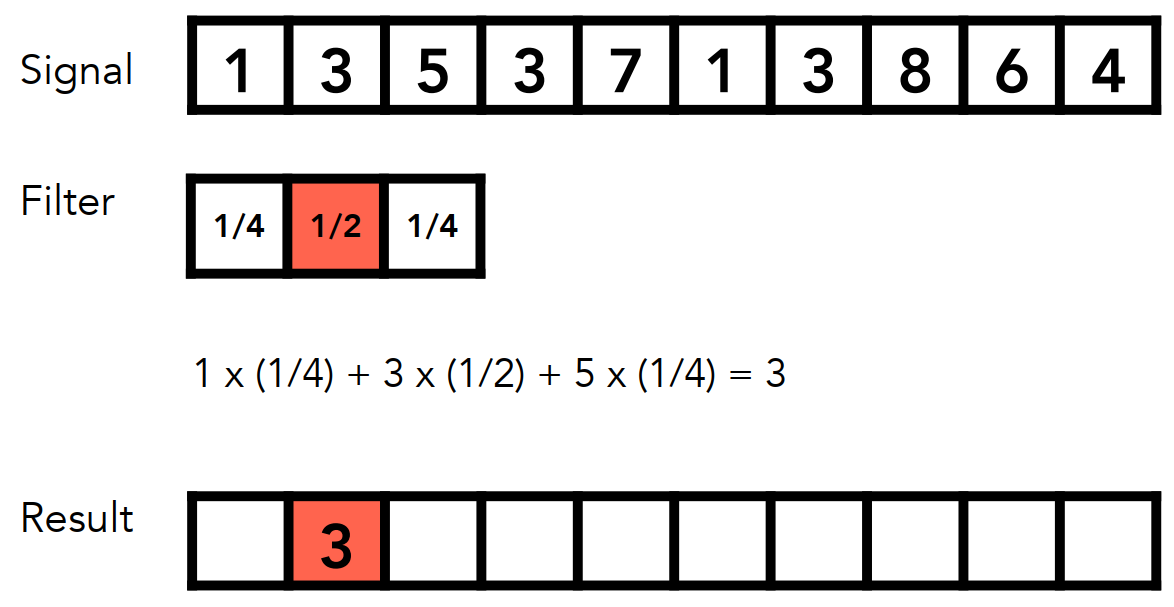
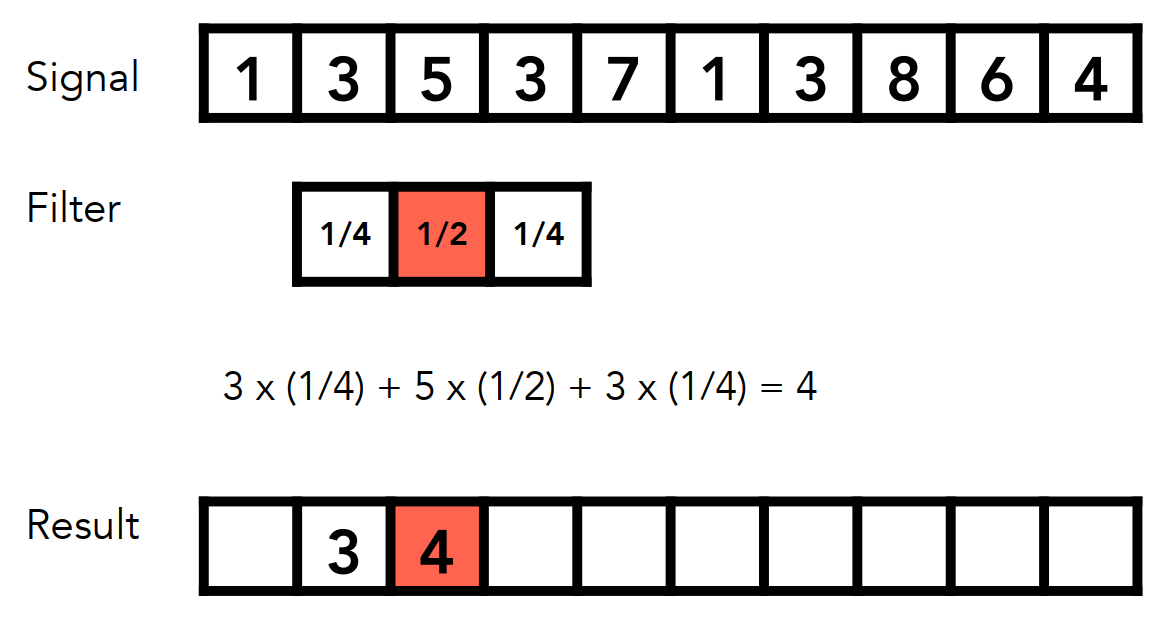
卷积操作

• 用一个3个单位的窗口（ 滤波器 ）作为 核 向右滑动；
• 核 中存储的信息是 权值 ；
• 在移动窗口的过程中对其进行加权线性运算（点乘）；
• 将结果写回窗口的中心格子。

向右滑动

TIPS ：在时域（spatial domain）上的卷积等效于在频域（frequency domain）上的乘积，反之亦然。

卷积的两种方案

• 选项1 ：
  • 在时域上进行卷积的滤波
• 选项2 ：
  • 将时域变换为频域（傅里叶变换）
  • 乘以卷积核的傅里叶变换
  • 将结果变换回时域（逆傅里叶变换）

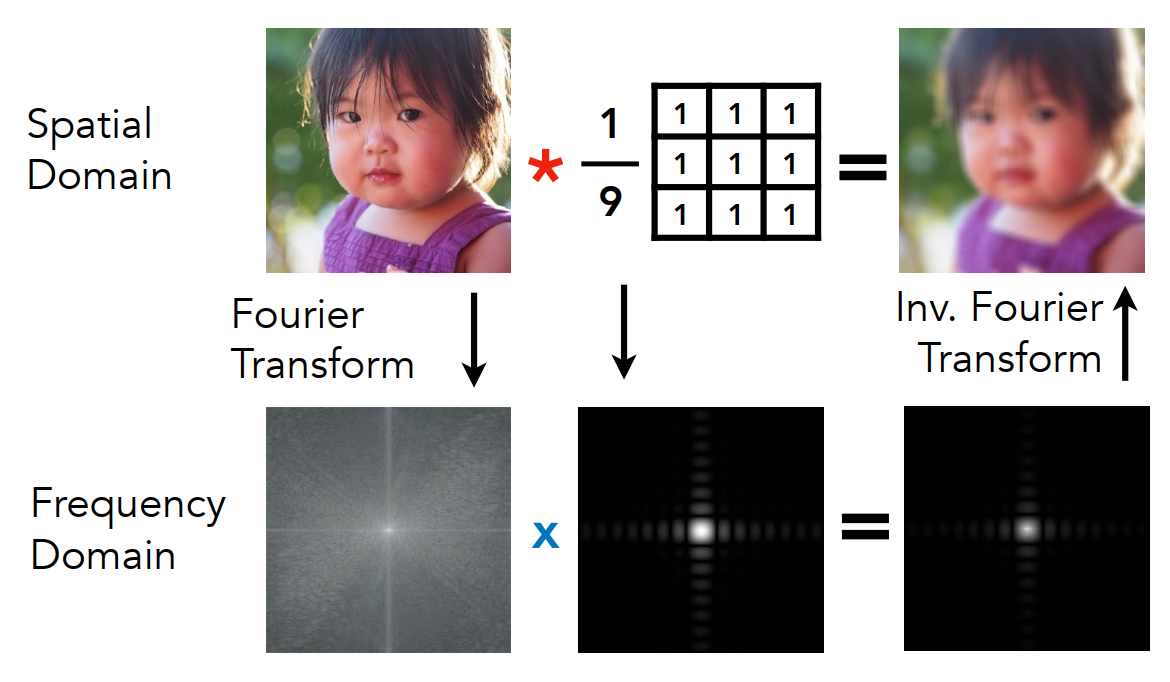
• 图中在频域（frequency domain）进行的操作，相对于对左下图做了一个低通滤波；
• $\times \cfrac{1}{9}$ 是做归一化操作，为了防止其颜色发生变化，否则图像会变得更加明亮。

盒子函数 = 低通滤波器

当时域上的盒子变大时，对应在频域上的图案反而变小了

• 相当于卷积核的规模变大，图案会变得更模糊

5.5 采样操作在频域上的表现形式

采样就是重复频域上的内容

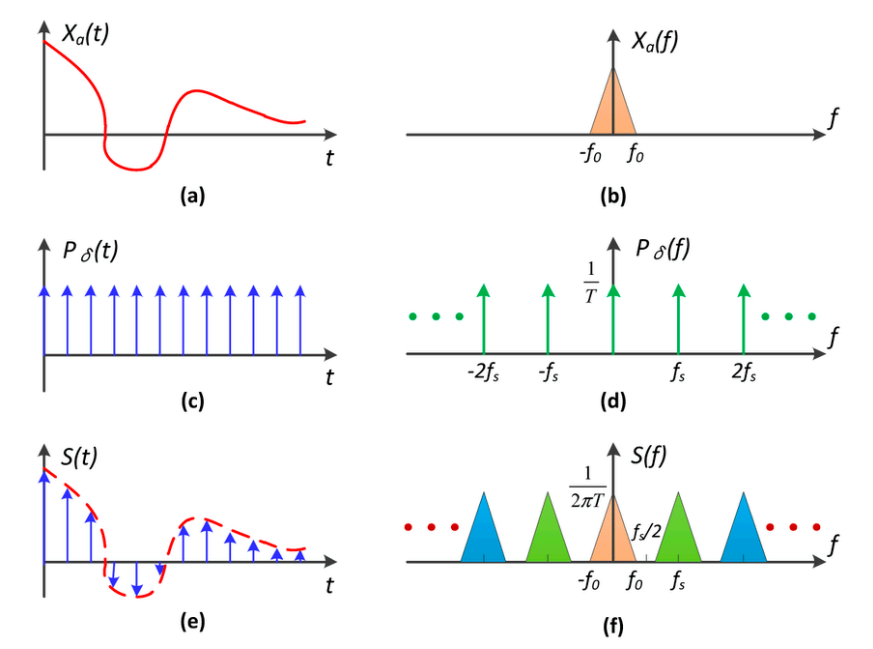
• 图（a）是某个连续的函数
• 图（b）假设是该函数映射到频域上的结果，即傅里叶变换的结果
• 图（c）中是 冲激函数 ，仅在若干位置上离散的存在值，其他位置的值为 0 ，此时我们可以用（c）函数乘以（a）函数，即获得（a）函数上离散的若干样本点，类似于一种掩码去对（a）函数进行采样；
• 图（d）即（c）函数映射到频域上的结果，会得到另一个间隔不同的冲激函数；
• 图（e）即（a）和（c）做了乘积之后，即采样之后留下的若干样本点；
• 图（f）即（e）函数映射到频域上的结果，同时由于“时域上的乘积等于频域上的卷积”，此时（e）函数同样也是（b）函数与（d）函数做卷积之后的结果。

NOTE ：

• 时域上的采样过程就是将待采样的连续函数乘以某个 冲激函数 ，最终得到采样结果；
• 在时域上进行的采样操作，在频域上则是根据 冲激函数 对（b）函数进行某种周期性的复制粘贴的操作，采样在频域上本质就是去重复原始信号的一个频谱。

6. 抗锯齿（Antialiasing）

6.1 图像由于采样而产生锯齿

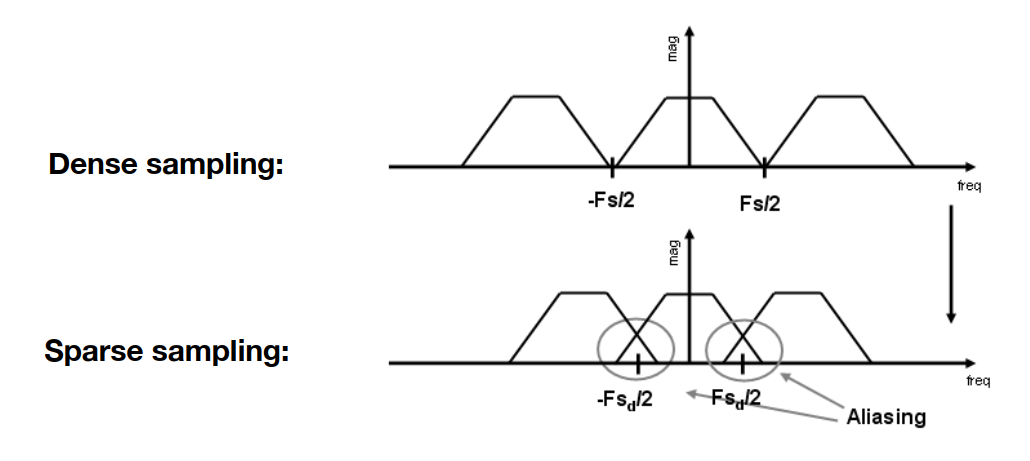
当 采样率不足（即采样速度不够快） 时，时域上的上的冲激函数的间隔过大，这会导致映射在频域上的冲激函数的间隔过小，即（d）函数的间隔过小，这会导致原始信号（b）在依据（d）进行卷积复制之后，产生“混叠”，发生了走样（锯齿化）。

6.2 抗锯齿的方案

选项 1：提高采样率

• 从根本上增大了傅里叶域上复制信号之间的间隔；
• 可以使用更高分辨率显示器、传感器、帧缓冲区…
• 但是：高分辨率意味着高成本。

选项 2 ：抗锯齿（Antialiasing）

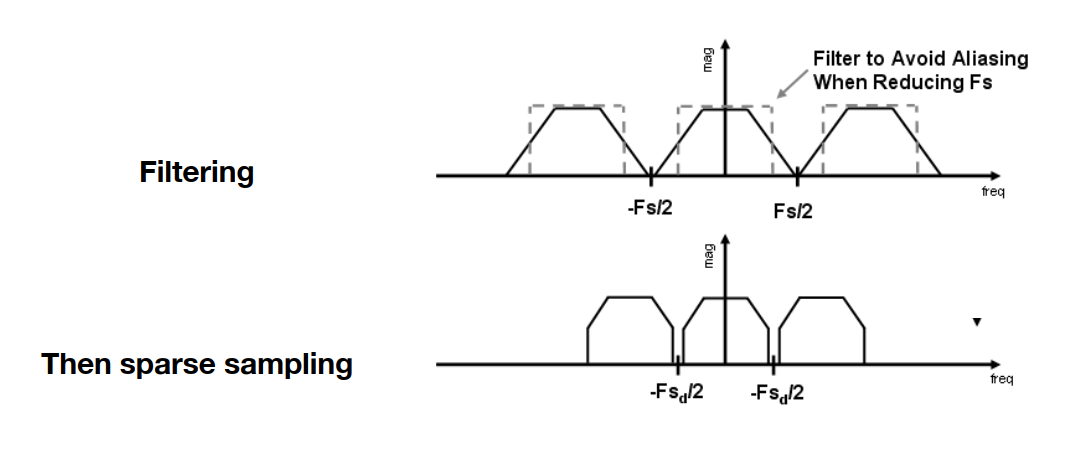
• 在对原始信号进行复制之前，先对其进行预处理，使待复制的内容“变窄”；
• 即在采样之前，将高频信号屏蔽掉，即使用低通滤波对其进行处理，在函数图像上的直观反映就是将原始信号的边缘砍掉；
• 宏观来讲，就是“先模糊，后采样”；
• 实际操作上就是用一个一定大小的盒子作为低通滤波器，对其进行卷积。

通过在像素区域上取平均值来进行抗锯齿：

• 使用 1 - 像素 盒子作为卷积核对 $f(x, y)$ 进行卷积操作；
• 将卷积的结果作为新值更改每个像素的中心值。

在栅格化一个三角形时：对三角形覆盖的某个像素区域做取平均值的操作，作为三角形覆盖的像素区域：

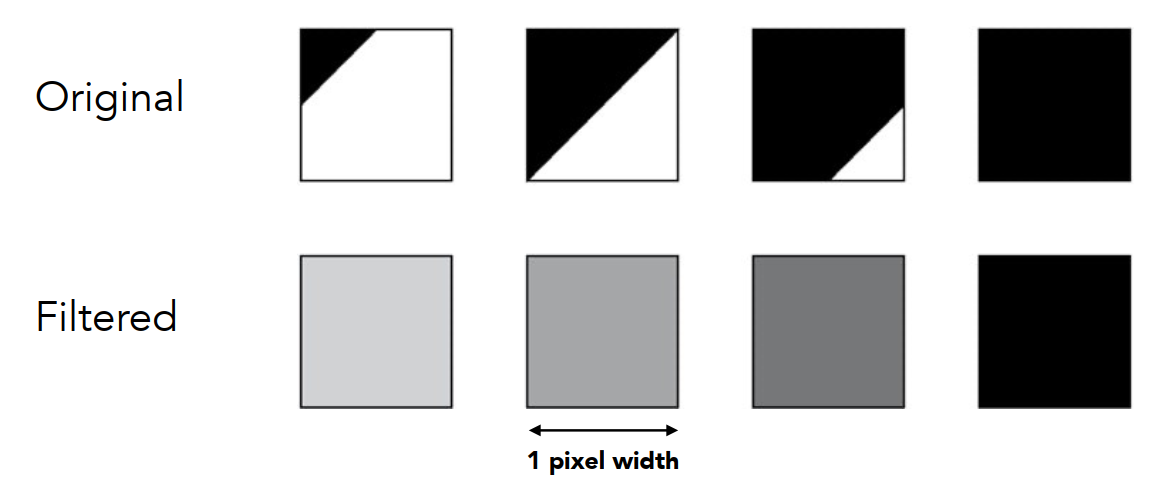
图中可见，

• 当原始图像中面积为 $\cfrac{1}{8}$ 时，亮度即为 87.5% ；
• 当原始图像中面积为 $\cfrac{1}{2}$ 时，亮度即为 50% 。

6.3 超采样抗锯齿 MSAA（Antialiasing By Supersampling）

通过对一个像素内的多个位置进行采样并取其值的平均值来近似 1 - 像素框过滤器（1 - pixel box filter）的效果：

图中将单个像素划分成 $4 \times 4$ 的更小的采样矩阵，计算每个检测点的覆盖情况之后，将其做一个平均。

• 一般情况下单个像素过大：

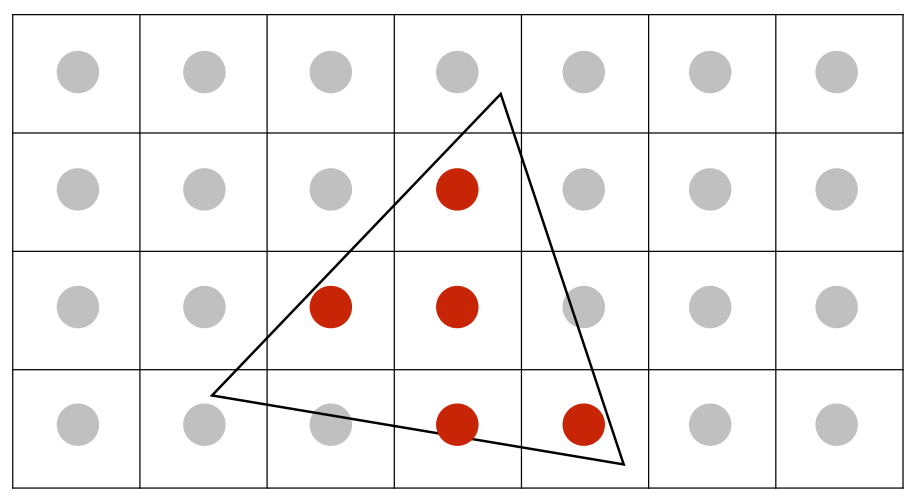
• 将单个像素划分成 $2 \times 2$ 的检测点后，计算其覆盖情况：

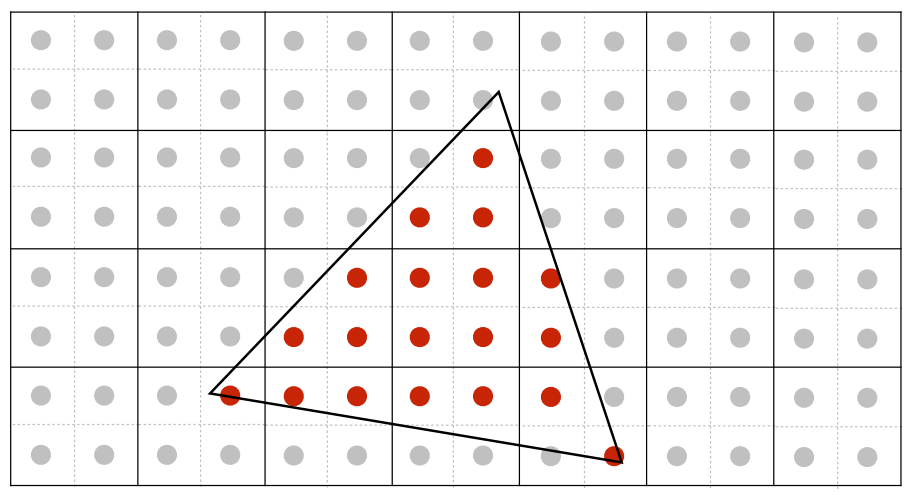
• 单个像素依据其中的4个检测点的三角形覆盖情况去做一个平均，计算每个像素的 覆盖率 ，调整亮度：

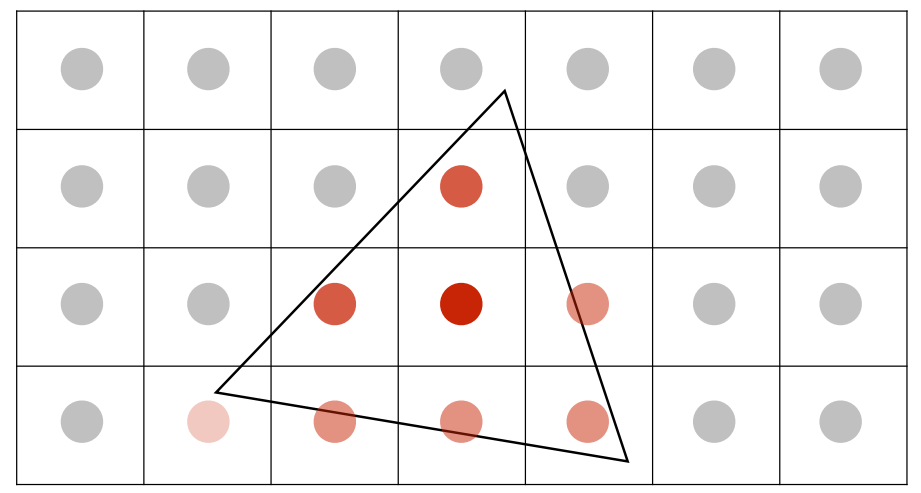
• 实际亮度数值如下

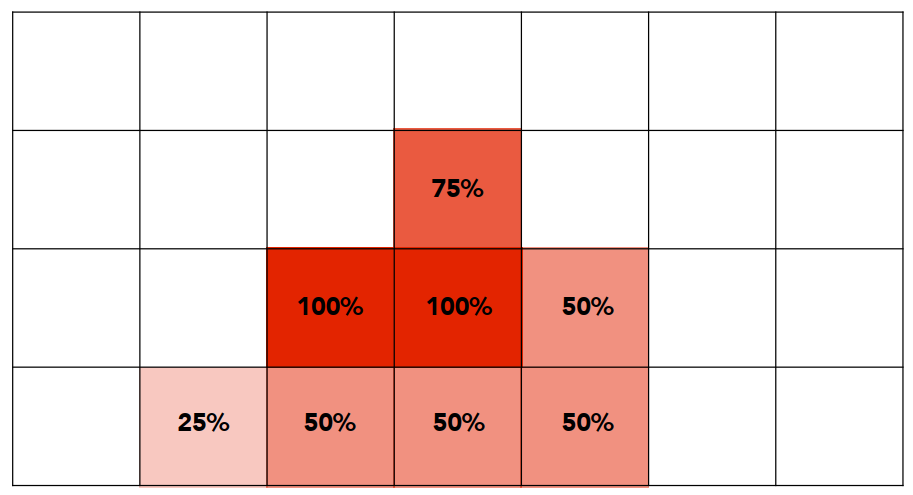
NOTE ：

• MSAA 实际上是一种模糊操作；
• 采样操作被简化了（隐含在其中）；
• MSAA 只是使用一种虚拟的高分辨率去做覆盖识别，从而计算出每个像素对应的覆盖率，但这一过程没有真正的提高物理分辨率；
• 工业中的 MSAA 对检测点进行的划分不是规则的，依靠一定的随机数对部分样本点进行一种复用，继而提高效率，即当开启 MSAA 之后，实际的渲染帧数不会掉到原来的 $\cfrac{1}{4}$ 。

6.4 其他的采样方式

6.4.1 FXAA —— 快速近似抗锯齿（Fast Approximate AA）

先获得锯齿图像，之后消除掉锯齿，但不是简单的对其模糊操作，FXAA 先通过图像匹配的方式找到锯齿边界，将该边界替换成无锯齿的边界。

6.4.2 TAA —— 时间性抗锯齿（Temporal AA）

• 依据上一帧的信息，我们依然使用像素内的一个点来检测是否在三角形内；
• 不过这个检测点是 动态变化的 ，比如在某个静止的场景中，理论上前后两帧的图像是一样的，但是实际渲染的这相邻两帧中，该像素中的检测点发生了变化，显然这会导致该像素是否被三角形覆盖的这一信息也发生变化，这便很可能使得该静态图在这两帧中渲染出来的图像不相同；
• 这时在渲染的整个过程中，某个像素是否被覆盖是不一样的；
• 也就是将 MSAA 中单个像素的多个检测点的检测操作平均分布在了时间轴上，过程中的每一帧会分别检测该像素中的每个不同的检测点。

把多次采样的过程分布到每一帧中去，每一帧都利用前面几帧保存下来的数据。

虚幻中的 Halton(2,3) ：

• 对之前帧中的采样信息进行累加：$P_n = \alpha \cdot c_n + (1 - \alpha) \cdot P_{n-1}$；
• 其中的系数 $\alpha$ 取一个较小值，例如 0.05 。

6.5 超分辨率/超采样（Super resolution / Super sampling）

• 当将某个图像从低分辨率强行转换为高分辨率时，采样率必定不足，会出现锯齿化的情况；
• 因此需要将其进行某种 “恢复” 操作；
• DLSS（深度学习超级采样） ：当把小图拉大的时候，必定会出现信息缺失的情况，这时可以用深度学习对缺失的信息细节进行补全。

7. 可见性

7.1 画家算法（Painter’s Algorithm）

灵感来自油画家的绘画过程：从远向近进行绘制，在帧缓冲区中一级一级的进行覆盖。

但是存在一个问题：深度的定义有一定的难度。

• 要求按照深度对 n 个三角形进行排序（时间复杂度 $O(n\log{n})$ ）

但存在如下这种不可解的深度顺序，在深度上存在互相遮挡的关系：

7.2 Z 缓冲

这是一种最终获胜算法（eventually won）

7.2.1 算法思路

• 存储每个样本（像素）的当前最小 z 值，即几何信息在该像素中最近的距离，如此这般对每个像素进行分析；
• 深度值需要一个额外的缓冲区；
  • 帧缓冲区（frame buffer）：存储颜色值，即最后的结果图像；
  • 深度缓冲区 / z缓冲区（depth buffer / z-buffer）：存储深度信息，在最后渲染帧缓冲区的图像时，提供渲染所需要的遮挡信息。

为了简化过程，假设：

• 视线朝着 $z$ 轴正方向，即 $z$ 的值总是正的；
• 更小的 $z$ 更近（深度越浅）；
• 更大的 $z$ 更远（深度越深）。

NOTE ：

• 右图是深度缓冲区，离 Camera 近的部分显得越黑，离 Camera 远的部分显得越白。

7.2.2 深度缓冲区算法（伪代码）

Initialize depth buffer to ∞
During rasterization:

  for (each triangle T)
    for (each sample (x,y,z) in T)
      // 找到当前最接近的样本
      // 若当前深度比 zbuffer 中对应的深度更近，对 zbuffer 更新
      if (z < zbuffer[x,y])
        // 更新帧缓冲区
        framebuffer[x,y] = rgb;
        // 更新深度缓冲区
        zbuffer[x,y] = z;
      else
        // 什么都不做，该样本被堵塞了
        ;

• 一开始将深度缓冲区初始化为无限远；
• 对每个三角形进行光栅化；
• 若三角形在当前像素的 z 值比深度缓冲区中存储的对应的 z 值要小，则更新帧缓冲区和深度缓冲区。

7.2.3 算法示例

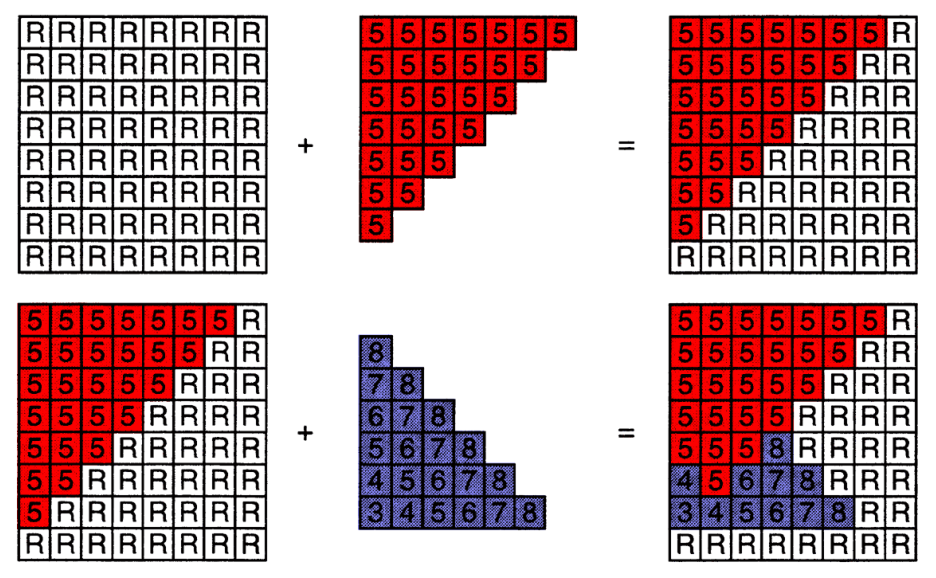
• 图中的方格是深度缓冲区；
• 图中的 R 我们设为无限大的值；
• 先将红色三角形进行光栅化，对深度缓冲区进行更新；
• 再对紫色三角形进行光栅化，对深度缓冲区进行更新，当紫色的数值更小时，对其进行更新，否则，保留原来的红色。

7.2.4 时间复杂度

• 三角形覆盖范围为常数；
• $n$ 个三角形对应的时间复杂度为 $O(n)$ ；
• 注意，该算法是通过迭代去找 $z$ 的最小值，并没有进行排序，所以时间复杂度是线性的。

在使用该算法时，假设 不会出现某两个三角形在某个像素的深度相同的情况 ，这样当三角形渲染的顺序发生变化时，深度缓冲区不会发生变化。

该假设是成立的，这是因为在计算机的实现过程中使用的是浮点型数，这样理论上是不会出现两个数值完全相同的浮点数。（然而实际上会出现该情况）