镜之国的爱丽丝
0%

01- 拉格朗日视角

发表于 更新于 分类于 ，

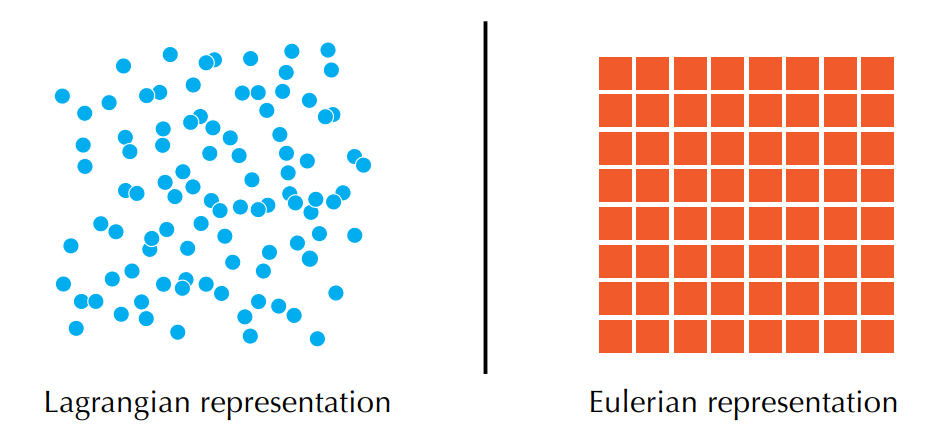
1. 拉格朗日视角 vs 欧拉视角

拉格朗日视角：其中的元素跟随一起移动。

欧拉视角 ：其中的元素固定在对应的地方，网格的点对应的速度。

screenShot.png

2. 弹簧质点系统

胡克定律

fij=−k(∥xi−xj∥2lij)xij^fi=∑jj≠ifij\begin{aligned} \bold{f}_{ij} &= -k(\Vert \bold{x}_i - \bold{x}_j \Vert_2 l_{ij})\hat{\bold{x}_{ij}} \\ \bold{f}_i &= \sum^{j \neq i}_j {\bold{f}_{ij}} \end{aligned}

牛顿第二定律

∂vi∂t=1mifi∂xi∂t=vi\begin{aligned} \cfrac{\partial \bold{v}_i}{\partial t} &= \cfrac{1}{m_i}\bold{f}_i \\ \cfrac{\partial \bold{x}_i}{\partial t} &= \bold{v}_i \end{aligned}

2.1 时间积分

前欧拉（显式）积分器 ：根据现有状态推测以后的状态

vt+1=vt+Δtftmxt+1=xt+Δtvt\begin{aligned} \bold{v}_{t+1} &= \bold{v}_t + \Delta t \cfrac{\bold{f}_t}{m} \\ \bold{x}_{t+1} &= \bold{x}_t + \Delta t \bold{v}_t \\ \end{aligned}

半隐式欧拉积分器 ：根据现有状态推测以后的状态，速度根据推测出的速度计算

vt+1=vt+Δtftmxt+1=xt+Δtvt+1\begin{aligned} \bold{v}_{t+1} &= \bold{v}_t + \Delta t \cfrac{\bold{f}_t}{m} \\ \bold{x}_{t+1} &= \bold{x}_t + \Delta t \bold{v}_{t+1} \\ \end{aligned}

2.2 代码

  1. 计算速度：vt+1=vt+Δtftm\bold{v}_{t+1} = \bold{v}_t + \Delta t \cfrac{\bold{f}_t}{m}
  2. 与地面碰撞（防止计算位移之后陷入地下）
  3. 计算位移：xt+1=xt+Δtvt+1\bold{x}_{t+1} = \bold{x}_t + \Delta t \bold{v}_{t+1}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
@ti.kernel
def substep():
    # Compute force and new velocity
    n = num_particles[None]
    for i in range(n):

        v[i] *= ti.exp(-dt * damping[None]) # 阻尼
        total_force = ti.Vector(gravity) * particle_mass
        
        for j in range(n):
            # 两个粒子有弹簧时
            if rest_length[i, j] != 0:
                x_ij = x[i] - x[j]
                total_force += -spring_stiffness[None] * (x_ij.norm() - rest_length[i, j]) * x_ij.normalized()
        v[i] += dt * total_force / particle_mass
        
    # Collide with ground
    for i in range(n):
        if x[i].y < bottom_y:
            x[i].y = bottom_y
            v[i].y = 0

    # Compute new position
    for i in range(num_particles[None]):
        x[i] += v[i] * dt

NOTE ：

  • 其中 Δt\Delta t 需要满足一下情况：

    Δt=cmk(c∼1)\Delta t = c\sqrt{\cfrac{m}{k}} (c \sim 1)

2.3 质点系统

隐式时间积分 ：

xt+1=xt+Δtvt+1vt+1=vt+ΔtM−1f(xt+1)\begin{aligned} \bold{x}_{t+1} &= \bold{x}_t + \Delta t \bold{v}_{t+1} \\ \bold{v}_{t+1} &= \bold{v}_t + \Delta t \bold{M}^{-1}\bold{f}(\bold{x}_{t+1}) \\ \end{aligned}

NOTE ：其中 $ \bold{M} $ 是质量矩阵。

消除 xt+1\bold{x}_{t+1} ：

vt+1=vt+ΔtM−1f(xt+Δtvt+1)\bold{v}_{t+1} = \bold{v}_t + \Delta t \bold{M}^{-1}\bold{f}(\bold{x}_t + \Delta t \bold{v}_{t+1}) \\

线性化（牛顿法的一步）：

vt+1=vt+ΔtM−1[f(xt)+∂f∂x(xt)Δtvt+1]\bold{v}_{t+1} = \bold{v}_t + \Delta t \bold{M}^{-1} \left[ {\bold{f}(\bold{x}_t) + \cfrac{\partial \bold{f}}{\partial \bold{x}}(\bold{x}_t)\Delta t\bold{v}_{t+1} } \right]

3. 形变

形变映射 ϕ\phi ：静止材料位置 ↦\mapsto 形变材料位置

xdeformed=ϕ(xrest)\bold{x_{deformed}} = \phi (\bold{x_{rest}})

形变梯度 F\bold{F} ：

F≔∂xdeformed∂xrest\bold{F} \coloneqq \cfrac{\partial \bold{x_{deformed}}}{\partial \bold{x_{rest}}}

Note ：

  • 平移过程中形变梯度保持不变：ϕ1=ϕ(xrest)\phi_1 = \phi(\bold{x_{rest}}) 和 ϕ1=ϕ(xrest)+c\phi_1 = \phi(\bold{x_{rest}}) + c 有相同的形变梯度

变形/静止体积比 JJ ：

J=det⁡(F)J = \det(\bold{F})

Note ：

  • 三维空间中，矩阵行列式的性质，即体积变化倍数

4. 弹性体

4.1 超弹性体（Hyperelasticity）

超弹性材料：应力 – 应变关系 由 应变能密度函数 定义 ：

Ψ=Ψ(F)\Psi = \Psi(\bold{F})

直观理解：Ψ\Psi 是惩罚形变的势函数。

应力 ：材料的内部弹性力。

应变 ：现在用 形变梯度 F\bold{F} 代替。

Note ：

  • Ψ\Psi 是应变能量密度函数
  • ϕ\phi 是形变映射

4.2 应力张量

应力：代表材料微元施加在其周围为材料微元的内力。

4.2.1 三种常用的应力张量

  • Piola - Kirchhoff 应力张量 （PK1）：

P(F)=∂Ψ(F)∂F\bold{P(F)} = \cfrac{\partial \Psi(\bold{F})}{\partial \bold{F}}

（计算简单，是在静止空间计算，需要变换到形变空间）
 

  • 基尔霍夫应力（Kirchhoff stress） ：τ\tau
     
  • 柯西应力张量（Cauchy stress tensor） ：σ\sigma
    （对称，因为角动量守恒）

4.2.2 关系式

  • τ=Jσ=PFT\tau = J\sigma = \bold{PF}^T
  • P=JσF−T\bold{P} = J\sigma\bold{F}^{-T}

Note：

  • F−T\bold{F}^{-T} ：补偿材料变形
  • 用 F−T\bold{F}^{-T} 替代 F−1\bold{F}^{-1} ：因为变换的是法向量 n\bold{n} 而不是 x\bold{x}

4.2.3 牵引力

  • t=σTn\bold{t} = \sigma^T\bold{n}

直观来说，将法向量乘以应力张量即可获得材料向周围微元施加的力。

4.3 弹性模量（各向同性材料）

  • 杨氏模量 ：应力张量与应变张量的比值

E=σϵE = \cfrac{\sigma}{\epsilon}

  • 体积模量 ：压强关于体积的变化，常用于液体

K=−VdPdVK = - V \cfrac{dP}{dV}

  • 泊松比 ：

ν∈[0.0,0.5)\nu \in [0.0,0.5)

Note ：

  • 辅助项具有负泊松比；
  • 泊松比为 0 时，拉长物体时，截面积不会发生变化；
  • 泊松比较大时，物体会尽量保持体积不变，例如在拉长物体时，物体会变细。

拉梅常数（Lamé parameters） ：

  • Lamé 第一参数： λ\lambda
    表示材料的压缩性，等价与体弹性模量或者杨氏模量
     
  • Lamé 第二参数： μ\mu
    表示材料的剪切模量，用 G 表示

换算公式 ：

  • K=E3(1−2ν)K = \cfrac{E}{3(1 - 2\nu)} （常用于可压缩液体）
     
  • λ=Eν(1+ν)(1−2ν)\lambda = \cfrac{E\nu}{(1 + \nu)(1 - 2\nu)}
     
  • μ=E2(1+ν)\mu = \cfrac{E}{2(1 + \nu)}

广义胡克定律 ：均匀和各向同性的材料

σ=2μϵ+λtr(ϵ)\sigma = 2 \mu \epsilon + \lambda tr(\epsilon)

5. 常见的超弹性模型

  • 经典的 MPM 方法将每个粒子看做材料的一个微元，材料的本构模型会有一个能量密度函数 Ψ\Psi ；
  • 对能量密度函数 Ψ\Psi 关于整个模型求积分，得到整个材料的势能；
  • 势能对材料点的形变梯度进行求导：P(F)=∂Ψ∂FP(\bold{F}) = \cfrac{\partial \Psi}{\partial \bold{F}} ；
  • 物理意义上来说，势能对位置求导的结果就是力，P(F)P(\bold{F}) 可以看做材料点的受力。

6.1 Neo-Hookean 模型

适用于各向同性材料

  • Ψ(F)=μ2∑i[(FTF)ii−1]−μlog⁡(J)+λ2log⁡2(J)\Psi(\bold{F}) = \cfrac{\mu}{2} \sum_i [(\bold{F}^T\bold{F})_{ii} - 1] - \mu \log(J) + \cfrac{\lambda}{2} \log^2(J)
     
  • P(F)=∂Ψ∂F=μ(F−FT)+λlog⁡(J)F−TP(\bold{F}) = \cfrac{\partial \Psi}{\partial \bold{F}} = \mu(\bold{F} - \bold{F}^T) + \lambda\log(J)\bold{F}^{-T}

因为 Neo-Hookean 模型容易造成能量流失，这时可以考虑 Corotated 模型。

FEM 中应用 Neo-Hookean 模型的示例代码 ：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
dim = 2

E, nu = 1000, 0.3
la = E * nu / ((1 + nu) * (1 - 2 * nu))
mu = E / (2 * (1 + nu))

element_V = 0.01

x = ti.Vector(dim, dt=real, shape=n_nodes, needs_grad=True)
v = ti.Vector(dim, dt=real, shape=n_nodes)

total_energy = ti.var(dt=real, shape=(), needs_grad=True)

# 计算势能
@ti.kernel
def compute_total_energy():
    for i in range(n_elements):
        ......# get F
        # NeoHookean
        I1 = (F @ F.transpose()).trace()
        # 防止 J 的值过小引起错误
        J = max(0.2, F.determinant())
        element_energy_density = 0.5 * mu * (I1 - dim) - mu * ti.log(J) + 0.5 * la * ti.log(J)**2
        total_energy[None] += element_energy_density * element_V

# 渲染循环
while True:
    for s in range(30):
        # 调用 taichi 的自动微分器
        # 定义的损失函数：compute_total_energy()
        # 函数值：total_energy
        # 变量值：x
        # 微分结果(i 点上的力) ：x.grad[i]
        # f = - \partial (total_energy) / \partial x
        with ti.Tape(total_energy):
            compute_total_energy()
        ......

Note ：

  • 在 FEM 中的势能（后续有详细说明）：

U(e)=∫eΨ(F(x))dx=VeΨ(Fe)U(e) = \int_e\bold{\Psi(F(x))\mathrm{d}x} = V_e\bold{\Psi(F_e)}

6.2 (Fixed)Corotated 模型

  • Ψ(F)=μ∑i(σi−1)2+λ2(J−1)2\Psi(\bold{F}) = \mu \sum_i(\sigma_i - 1)^2 + \cfrac{\lambda}{2}(J - 1)^2
     
  • P(F)=∂Ψ∂F=2μ(F−R)+λ(J−1)JF−TP(\bold{F}) = \cfrac{\partial \Psi}{\partial \bold{F}} = 2\mu(\bold{F} - \bold{R}) + \lambda(J - 1)J\bold{F}^{-T}

Note ：

  • σi\sigma_i 是 F\bold{F} 的奇异值。

6.3 MPM 教程

《The Material Point Method for Simulating Continuum Materials》

6. 有限元基础

有限元法 ：建立离散模型的 Galerkin 离散格式。

6.1 线性四面体（三角形）有限元法

线性四面体有限元（用于弹性）假设 形变映射 phiphi 是一个仿射变换，因此 形变梯度 F\bold{F} 在单个四面体单元内是恒定的，对单个元素来说：

xdeformed=Fxrest+p\bold{x_{deformed}} = \bold{Fx_{rest}} + \bold{p}

对于每个元素 ee ，对能量密度函数求体积的积分，可以计算其弹性势能：

U(e)=∫eΨ(F(x))dx=VeΨ(Fe)U(e) = \int_e\bold{\Psi(F(x))\mathrm{d}x} = V_e\bold{\Psi(F_e)}

  • 其中 形变梯度 F\bold{F} 在元素 ee 上是个常数 Fe\bold{F_e} ，即 Ψ(Fe)\bold{\Psi(F_e)} 也为常数，因此可以直接得到积分结果。

6.2 计算形变梯度

xdeformed=Fxrest+p\bold{x_{deformed}} = \bold{Fx_{rest}} + \bold{p}

在 2D 三角形元素（三维空间中是四面体元素）中，设：

  • 静止时的顶点位置： arest\bold{a_{rest}} ，brest\bold{b_{rest}} ，crest\bold{c_{rest}} ；
  • 变形后的顶点位置：adeformed\bold{a_{deformed}} ，bdeformed\bold{b_{deformed}} ，cdeformed\bold{c_{deformed}} 。

因为在线性三角形元素中 F\bold{F} 是常数，则有：

adeformed=Farest+pbdeformed=Fbrest+pcdeformed=Fcrest+p\begin{aligned} \bold{a_{deformed}} &= \bold{Fa_{rest}} + \bold{p} \\ \bold{b_{deformed}} &= \bold{Fb_{rest}} + \bold{p} \\ \bold{c_{deformed}} &= \bold{Fc_{rest}} + \bold{p} \end{aligned}

消除 p\bold{p} ：

(adeformed−cdeformed)=F(arest−crest)(bdeformed−cdeformed)=F(brest−crest)\begin{aligned} (\bold{a_{deformed}} - \bold{c_{deformed}}) &= \bold{F}(\bold{a_{rest}} - \bold{c_{rest}}) \\ (\bold{b_{deformed}} - \bold{c_{deformed}}) &= \bold{F}(\bold{b_{rest}} - \bold{c_{rest}}) \end{aligned}

现在 F2×2\bold{F}_{2\times 2} 有四个线性约束：

B=[arest−crest∣brest−crest]−1D=[adeformed−cdeformed∣bdeformed−cdeformed]F=DB\begin{aligned} \bold{B} &= [\bold{a_{rest}} - \bold{c_{rest}} | \bold{b_{rest}} - \bold{c_{rest}}]^{-1} \\ \bold{D} &= [\bold{a_{deformed}} - \bold{c_{deformed}} | \bold{b_{deformed}} - \bold{c_{deformed}}] \\ \bold{F} &= \bold{D}\bold{B} \end{aligned}

其中 B\bold{B} 在整个物理过程中是常数。因此可进行预计算。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
B = ti.Matrix(dim, dim, dt=real, shape=n_elements)
vertices = ti.var(dt=ti.i32, shape=(n_elements, 3))

@ti.func
def compute_D(i):
    a = vertices[i, 0]
    b = vertices[i, 1]
    c = vertices[i, 2]
    return ti.Matrix.cols([x[b] - x[a], x[c] - x[a]])

@ti.kernel
def compute_B():
    for i in range(n_elements):
        B[i] = compute_D(i).inverse()

@ti.kernel
def compute_total_energy():
    for i in range(n_elements):
        D = compute_D(i)
        F = D @ B[i]
        ......

6.3 显式时间积分

vt+1,i=vt,i+Δtft,imixt+1,i=xt,i+Δtvt+1,i\begin{aligned} \bold{v}_{t+1,i} &= \bold{v}_{t,i} + \Delta t\cfrac{\bold{f}_{t,i}}{m_i} \\ \bold{x}_{t+1,i} &= \bold{x}_{t,i} + \Delta t\bold{v}_{t+1,i} \end{aligned}

  • vt,i\bold{v}_{t,i} 和 xt,i\bold{x}_{t,i} 存储在顶点中。

弹性势能对位置求导，结果的相反值即为顶点的受力：

ft,i=−∂U∂xi=−∑e∂U(e)∂xi=−∑eVe∂Ψ(Fe)∂Fe∂Fe∂xi=−∑eVeP(Fe)∂Fe∂xi\begin{aligned} \bold{f}_{t,i} &= - \cfrac{\partial U}{\partial \bold{x}_i} \\ &= -\sum_e \cfrac{\partial U(e)}{\partial \bold{x}_i} \\ &= -\sum_e V_e \cfrac{\partial\Psi(\bold{F}_e)}{\partial\bold{F}_e} \cfrac{\partial\bold{F}_e}{\partial{\bold{x}_i}} \\ & = -\sum_e V_e \bold{P}(\bold{F}_e)\cfrac{\partial\bold{F}_e}{\partial{\bold{x}_i}} \end{aligned} 

1
2
3
4
5
6
7
@ti.kernel
def integrate():
    for p in x:
        ...... # 碰撞检测
        # 显式时间积分
        v[p] = (v[p] + ((-x.grad[p] / node_mass) + ti.Vector([0, -10])) * dt) * math.exp(dt * -6)
        x[p] += dt * v[p]
  • 其中：

vt+1,i=(vt,i+ft,i+migmiΔt)e−6Δt\bold{v}_{t+1,i} = \left(\bold{v}_{t,i} + \cfrac{\bold{f}_{t,i}+m_i g}{m_i} \Delta t \right) e^{-6 \Delta t}

6.4 隐式时间积分

[I−Δt2M−1∂f∂x(xt)]vt+1=vt+ΔtM−1f(xt)\left[ \bold{I} - \Delta t^2 \bold{M}^{-1} \cfrac{\partial \bold{f}}{\partial \bold{x}}(\bold{x}_t) \right] \bold{v}_{t+1} = \bold{v}_t + \Delta t \bold{M}^{-1} \bold{f} (\bold{x}_t)

力的微分计算：

∂f∂x=−∂2Ψ∂x2 \cfrac{\partial \bold{f}}{\partial \bold{x}} = - \cfrac{\partial^2 \bold{\Psi}}{\partial \bold{x}^2}