1. 相关概念
1.1 快速多极算法简介
快速多极展开算法(FMM)最初是用来处理大量粒子之间相互影响的问题,也可以用来计算基于 位势理论 的拉普拉斯方程的数值解,同时也可用来处理泊松方程。
同理,我们也可以用相关场的求解过程来辅助理解 FMM 求解泊松方程的这一过程,该处以多体系统的静电场为例。
1.2 静电场
1.2.1 公式的离散形式
对于空间 N 个带电粒子构成的系统,第 i 个粒子所在位置的静电势 Φ(xi) :
Φ(xi)=j=1,j=i∑Nrijmj
所受到的静电力 E(xi) :
E(xi)=j=1,j=i∑Nmjrij3xi−xj=j=1,j=i∑Nmj∥xi−xj∥3xi−xj
Note :
- xi :表示第 i 个粒子所在位置;
- mj :表示第 j 个粒子所占权重,与带电量 qj 成正比;
- rij :表示第 i 个粒子和第 j 个粒子之间的距离;
- ∥⋅∥ :表示两点间的距离;
- 求解 E(xi) 相当于对 i 粒子与 i 粒子以外的所有粒子的相互力做一个累和,复杂度为 O(N) ,同理,如果对全部 N 个粒子都使用该方式进行求解,复杂度高达 O(N2) 。
1.2.2 公式的积分形式
对于空间连续介质问题,假设粒子是连续分布在空间曲面 S 上,则离散的多粒子系统可以过渡到连续介质系统。在点 x 处受到整个曲面的势为:
Φ(x)=∫S∣x−y∣m(y)dS(y),y∈S
点 x 处受到整个曲面的力为:
E(x)=∫Sm(y)∣x−y∣3x−ydS(y),y∈S
Note :
- ∣⋅∣ :表示两点间的距离。
1.2.3 公式的复势形式
课程中为了式子尽可能的直观,主要是以该表达方式为例。
对于单个粒子产生的场
位于复平面上的点 zj 的平面点电荷 qj 在点 z 的复势:
fj(z)=2πϵ0−qjln(z−zj)
其中的实部为势函数:
ϕj(z)=Refj(z)=2πϵ0qjRe(ln(z−zj))
Note :
- 虚部为通量函数,由于该处我们仅讨论势函数,故忽略。
对于 j 个粒子组成的系统产生的场
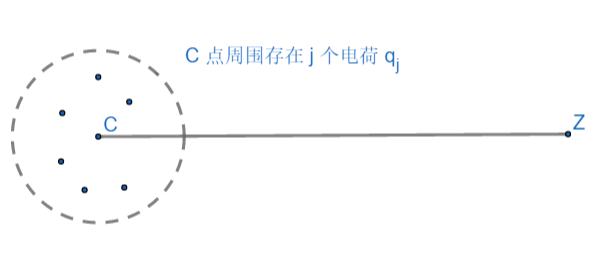
点 c 附近的 m 个电荷对点 z 的势(直接累和):
ϕ(z)=2πϵ01Rej=1∑mqj(ln(z−zj))
该处简化为:
ϕ(z)=j=1∑mqjln(z−zj)(1)
将 ln(z−zj) 在点 z 处做泰勒级数展开,即:
ln(z−zj)=lnz−k=1∑∞kzkzjk(2)
将公式(2)代入公式(1),得到:
ϕ(z)=j=1∑mqjlnz−j=1∑mk=1∑∞kzkqjzjk(3)
不妨定义一个总电荷变量 Q 、 Qk 如下:
⎩⎪⎨⎪⎧Q=∑j=1mqjQk=−∑j=1mkqjzjk(4)
将(4)式代入(3)式,得到:
ϕ(z)=Qlnz−k=1∑∞zkQk(5)
对于 ln(z−zj) 的泰勒展开:
ln(z−zj)=0!lnz+(−zj)1!z1+(−zj)22!−z21+(−zj)33!(−1)22z31+⋯+(−zj)kk!(−1)k−1(k−1)!zk1+⋯=lnz−k=1∑∞kzkzjk
1.3 相关方程
1.3.1 拉普拉斯方程(调和函数)
如果一个函数满足拉普拉斯方程:
∇2Φ=∂x2∂2Φ+∂y2∂2Φ+∂z2∂2Φ=0
则称它为调和函数。
1.3.2 球面调和函数(球谐函数)
球坐标下的三维拉普拉斯方程:
r21∂r∂(r2∂r∂Φ)+r2sinθ1∂θ∂(sinθ∂θ∂Φ)+r2sin2θ1∂ϕ2∂2θ=0
用分离变量法解出的该方程的标准解为:
Φ=n=0∑∞m=−n∑n(Lnmrn+rn+1Mnm)Ynm(θ,ϕ)
Note :
- n 次球面调和函数 : Ynm(θ,ϕ)rn ;
- -(n+1) 次球面调和函数 :Ynm(θ,ϕ)/rn+1 ;
- 系数 Lnm 、 Mnm 称为 展开的矩 ,它们仅与电荷的本质属性有关(电荷的位置和带电量);
- 在多极展开中,系数 Lnm=0 ;
- 在局部展开中,系数 Mnm=0 ;
Ynm(θ,ϕ)=(n+∣m∣)!(n−∣m∣)!⋅Pn∣m∣(cosθ)eimϕ
- 其中 Pn∣m∣(cosθ) 的值可通过以下递推式求得:
⎩⎪⎪⎨⎪⎪⎧(2n+1)xPnm(x)=(n−m+1)Pn+1m(x)+(n+m)Pn−1mPnm+2(x)+2(m+1)x2−1xPnm+1(x)=(n−m)(n+m+1)Pnm(x)
2. 快速多级算法
2.1 关键思路
- 有一个指定的可接受的计算精度 ϵ ;
- 将空间分层细分为 源(sources) 的 平面(panels) 或 簇(clusters) ;
- 一个 核函数(kernel) k(x,y) 的远场展开,其中源(source)和评价点(evaluation points)的影响是分开的;
- 远场展开到局部展开的转换。
2.2 网格分层构建
- 选取一个能够将所有粒子都包含进去的正方形平面作为计算的定义域,对其进行分成;
- 规定该定义域为第 0 层网格(即最大的单个方格);
- 第 L+1 层网格是第 L 层网格进行 2×2 的划分,同时,从第 L 层中的某个网格 box 中划分出来的 4 个网格是网格 box 的子结点;
- 显然,对于第 L 层,所有网格的个数为 4L (如果是三维情况,八叉树情况下网格个数为 8L )。
2.3 网格之间的关系
- 以下图片来自 《快速多极边界元法在动力学问题中的若干应用_姚振汉》
2.3.1 邻接网格(nearest box)
邻接网格(nearest box) :对于第 L 层的某个网格 S1 ,其 “邻接网格” 是同第 L 层且有共同边界点的网格,图中的 S2 即为 S1 的 “邻接网格” 。
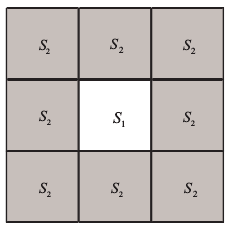
2.3.2 分离网格对(well separated pairs)
分离网格对(well separated pairs) :两个网格在同一层,且不是 “邻接网格” ,则称为两个网格是 分离关系(well separated) 。
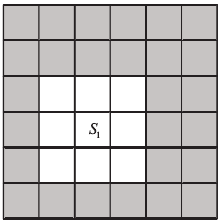
2.3.3 交互列表(interaction list)
交互列表(interaction list) :对于第 L 层的某个网格 S1 , S1 的父结点的 “邻接网格” 的子结点的集合称之为 S1 的 “交互列表” ,同时集合中的网格与 S1 是 “分离关系” 。
- “交互列表” 是一组结点的集合,这组结点不是 S1 的 “邻接网格” ,是至少间隔一个网格的;
- 在某层,对于其中的每一个网格,均存在一组对应的 “交互列表” ;
- “交互列表” 中的网格,是当前层待多极展开计算的网格。
3. 算法流程概述
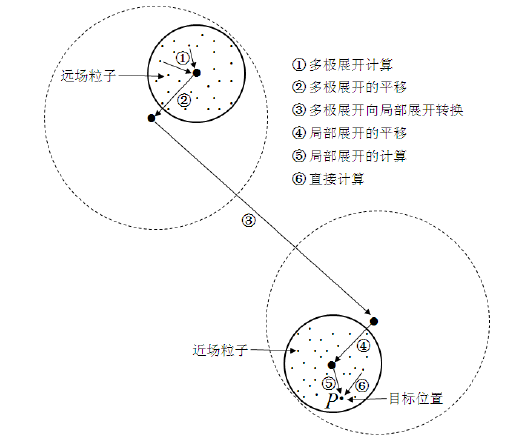
- 图片来自 《基于快速多极展开算法的直升机旋翼尾迹计算分析_丁国华》
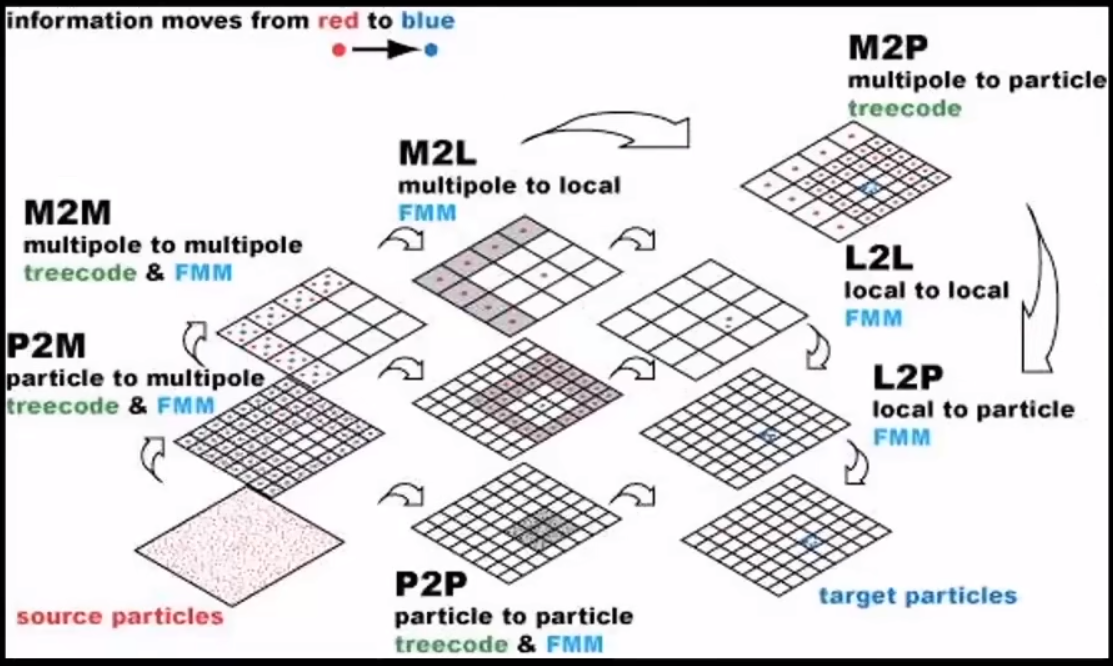
3.1 Tree Code(NlogN)
3.1.1 递归起始条件
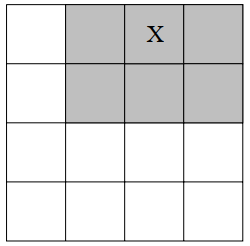
- 首先,从第 0 层到第 1 层,是一个 2×2 的网格,不存在 “分离网格对”;
- 在第 2 层,存在若干个 “分离网格对” ,对其使用多极展开计算交互;
- 计算分两个部分:
- 计算网格 X 内部粒子之间的交互;
- 计算白色网格(与网格 X 是 “分离关系” 的网格)的多极展开;
- 网格 X 以外的灰色网格(网格 X 的“邻接网格”)不计算。
- 在计算过程中,需要考虑误差的界限,对于精度 ϵ ,展开项数 p 为 p=log2(1/ϵ) 。
3.1.2 递归过程
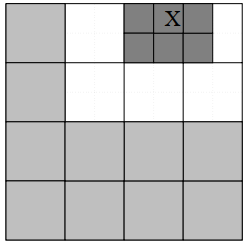
- 显然,在第 2 层中,每个网格的粒子簇和其邻接网格中粒子簇的交互还需要去计算。
接下来讨论第 3 层:
- 在第 3 层中,父网格的邻接网格以外的网格对网格 X 的交互已经计算完毕(图中亮灰色网格,对应的第 2 层的白色网格);
- 在当前层中,网格 X 与其邻接网格的交互无法计算(图中深灰色网格);
- 排除以上两个部分,剩下的网格即是上述定义的 “交互列表” (图中白色网格),此时是 “分离关系”,可以使用多极展开计算交互。
Note :
- 第 3 层中的网格 X 可以看成是第 2 层中的网格 X 进一步的细分,目标粒子同时存在于这两个网格中;
- 第 3 层中的亮灰色网格(“已计算网格”)是在第 2 层中已经计算完毕的白色网格(“交互列表”,或者形象的称之为“待计算网格”);
- 第 2 层中的灰色网格(“邻接网格”),有一部分在第 3 层中变成了白色(“交互列表”),此时,变成白色的部分可以在当前层进行多极展开计算;
- 通过这种方式进行递归,将未计算交互的部分(即上一层的 “邻接网格” 部分)一层层的定义成白色(“交互列表”)进行计算,对于目标粒子来说,来自 “远场” 的交互,像是一个从外向内,越来越薄的洋葱皮。
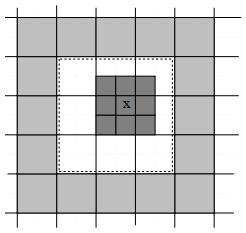
3.1.3 算法分析
整体角度 :
- 递归树的高度为 logN ;
- 每一层的工作量约为 O(N) ,对于每个多极展开的项数为 p ,创建所有展开式的操作数为 Np ;
单个粒子的角度 :
- 最多有 27 个网格需要进行展开计算(27 是 “交互列表” 的最大网格数),因此操作数为 27Np :
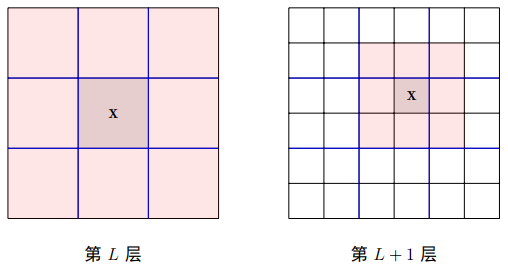
- 图中红色网格代表的无法计算的 “邻接网格” ;
- 在第 L+1 层中,白色网格部分是当前层需要进行计算交互的 “交互列表”,同时也是第 L 层中的 “邻接网格” 的一部分;
- 可见当网格 X 处于中间方位的时候,白色网格部分最大值为 27 。
递归出口 :
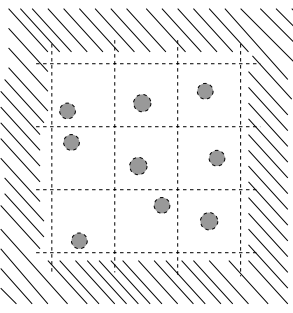
- 在最下面一层,大概划分出了 4log4N=N 个网格;
- 还剩下目标粒子所在网格的 “邻接网格” 未计算交互;
- 根据均匀性假设,每个网格的粒子数为 O(1) ,最后一步是目标粒子所在的网格与周围 8 个 “邻接网格” 进行直接计算,操作数为 8N 。
总的时间花费为:
28NplogN+8N
3.1.4 自适应算法
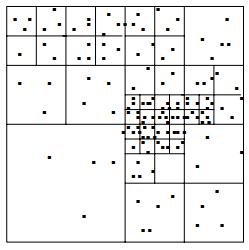
当粒子的分布是不均匀的情况下,我们可以使用一种自适应的数据结构,确保每个网格都含有粒子,且粒子数目适中。
在网格划分的过程中,检查每个网格是否包含有粒子:
- 若存在粒子,则继续划分该网格;
- 若不存在粒子,将该网格及其兄弟网格从树中剪枝,回溯到父网格,提前结束递归,不参与后续的划分操作。
3.2 快速多极展开
向上遍历 :
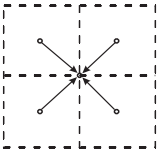
向下遍历 :
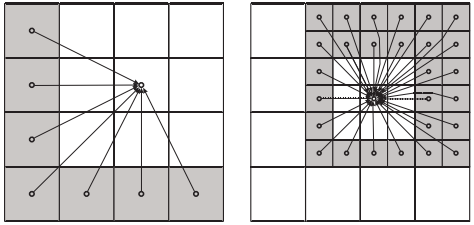
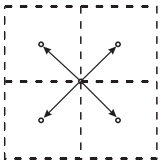
3. 多极展开计算(P2M)

计算一个远场区域内的 m 个电荷对点 z 的势:
ϕ(z)=j=1∑mqjlnz−j=1∑mk=1∑∞kzkqjzjk(3)
令远场中心点的电荷为远场的总电荷 Q :
⎩⎪⎪⎨⎪⎪⎧Q=∑j=1mqjQk=−∑j=1mkqjzjk=−Qk∑j=1mzjk(4)
用式(4)替换式(3)中的对应系数:
ϕ(z)=Qlnz+k=1∑∞zkQk(5)
当然,在实际实现多极展开时,需要确定多极展开的项数 p , p 的选取决定了计算结果的精度,这里直接表示在式中泰勒展开的级数:
ϕ(z)=Qlnz+k=1∑pzkQk(6)
4. 多极展开的平移(M2M)
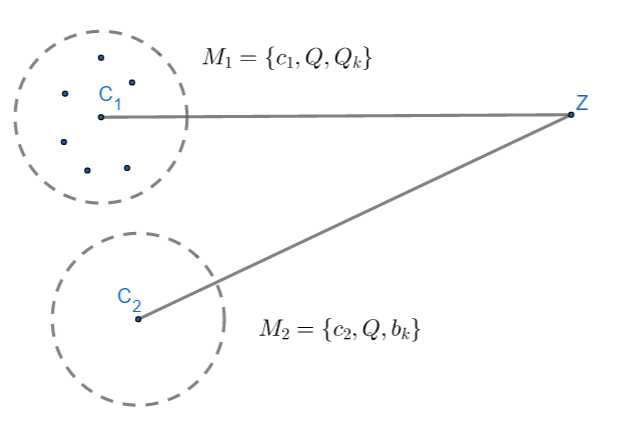
设在中心 c1 的半径圆内,存在一组强度为 q1,q2,⋯,qj 的 j 个电荷引起的势的多极展开,即 M1 网格,其在点 z 产生的势为:
ϕc1(z)=Qln(z−c1)+k=1∑p(z−c1)kak(7)
其中的高阶项 ak :
ak=−Qk∑j=1m(zj−c1)k
这里我们需要寻找到一个 M1↦M2 的变换,在网格 M2 处找到一个展开式 ϕC1(z) 使得 ϕC1(z)=ϕC2(z) ,相当于用 ϕC1(z) 在点 c2 处进行泰勒展开:
ϕc2(z)=Qln(z−c2)+k=1∑pzkbk(8)
其关键在于高阶项 bk , bk 是对 Qk 的一个泛化:
bk=−kQ(c1−c2)k+i=1∑kQi(c1−c2)k−i(k−1i−1)(9)
- 对一个分布若干粒子的平面进行网格划分;
- 对每个格子的中心点进行计算,主要计算 Q , Qk , ϕc(z) ;
- 对于离格子较远处的某个点 z (换句话说,该格子对于这个点 z 来说是个 远场 ),该点受到的格子产生的势的影响 ϕc(z) ,可被 Q , Qk 近似表示,见式(6);
- 对于每一层,均执行一次向上抽象,即计算 Q , Qk , ϕc(z) 。
4.2 多极展开公式(multipole )
5. 多极展开向局部展开变换(M2L)
6. 局部展开的平移(L2L)
7. 局部展开计算
球坐标系
球坐标系向直角坐标系的转换
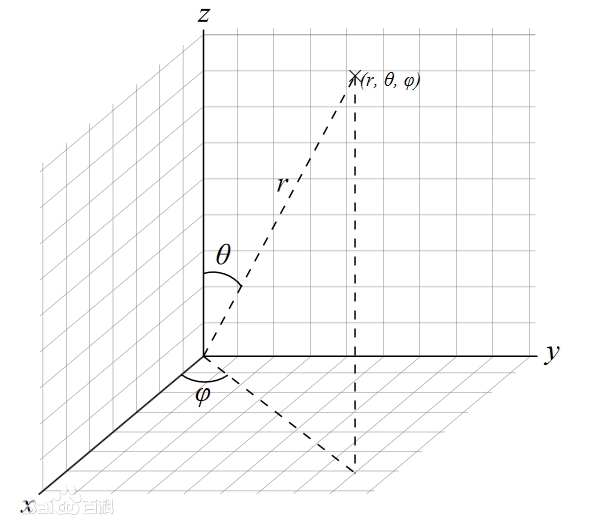
球坐标 (r,θ,φ)↦ 直角坐标 (x,y,z)
⎩⎪⎨⎪⎧x=rsinθcosφy=rsinθsinφz=rcosθ
球坐标系下两直线的夹角
若已知球坐标系中两个方向分别为 r1(1,θ1,ϕ1) 和 r2(1,θ2,ϕ2) ,求它们之间的夹角 α 。
⎩⎨⎧r1=(sinθ1cosϕ1,sinθ1sinϕ1,cosθ1)r2=(sinθ2cosϕ2,sinθ2sinϕ2,cosθ2)
- 再计算两个单位向量之间的夹角 α :
cosα=r1⋅r2=sinθ1cosϕ1sinθ2cosϕ2+sinθ1sinϕ1sinθ2sinϕ2+cosθ1cosθ2=sinθ1sinθ2(cosϕ1cosϕ2+sinϕ1sinϕ2)+cosθ1cosθ2=sinθ1sinθ2cos(ϕ2−ϕ1)+cosθ1cosθ2
参考资料 :
















