镜之国的爱丽丝
0%

04 - 旋转变换

发表于 更新于 分类于

1. 方位和角位移

我们知道不能用绝对坐标来描述物体的 位置 ，要描述物体的 位置 ，必须把物体放置于特定的参考系中。

描述 位置 实际上就是描述相对于给定参考点（通常是坐标系的原点）的 位移 。

同样，描述物体 方位 时，也不能使用绝对量。
与位置只是相对已知点的位移一样，方位是通过于相对已知方位（通常称为“单位”方位或“源”方位）的旋转来描述的。

  • 旋转的量称作角位移。
  • 换句话说，在数学上描述 方位 就等价与描述 角位移 。

整理如下：

  • 方位：

    • 表示的是一种静态的状态；
    • 当用矩阵表示方位时，此时矩阵表示的是一个“点”，而该点的坐标就是原点进行矩阵表示的旋转之后所在的地方。即描述 方位 实际上就是描述相对于给定参考点（通常是坐标系的原点）的 角位移 。

  • 角位移：

    • 表示的是一种动态的过程；
    • 当用矩阵表示角位移时，旋转变换的量即是角位移。

具体来说，我们用矩阵和四元数来表示“角位移”，用欧拉角来表示“方位”。

2. 矩阵形式 —— 用矩阵描述旋转变换

3D 中，描述坐标系中 方位 的一种方法就是列出这个坐标系的 基向量 ，而这些基向量是相对于其他坐标系进行描述的。
这些基向量构成一个 3×33 \times 3 矩阵，然后就能用矩阵形式来描述 方位 。

换言之，能用一个 旋转矩阵 来描述这两个坐标系之间的相对方位，这个旋转矩阵用于把一个坐标系中的向量转换到另一个坐标系中。

3. 基本旋转矩阵

3.1 绕 < 3 - 轴 > 旋转

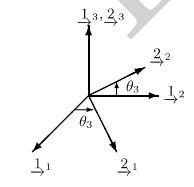
screenShot.png

先将 F1→\underrightarrow{F_1} 看做基向量空间 II ，可推出：

{21⃗T=[cos⁡θ3sin⁡θ30]22⃗T=[−sin⁡θ3cos⁡θ30]23⃗T=[001]\begin{cases} &\vec{2_1}^{T} = \begin{bmatrix} \cos{\theta_3} & \sin{\theta_3} & 0 \end{bmatrix} \\[2ex] &\vec{2_2}^{T} = \begin{bmatrix} -\sin{\theta_3} & \cos{\theta_3} & 0 \end{bmatrix} \\[2ex] &\vec{2_3}^{T} = \begin{bmatrix} 0 & 0 & 1 \end{bmatrix} \end{cases}

可得绕 < 3 - 轴 > 旋转的 旋转矩阵 C3\bold{C_{3}} 为：

C3=C21=[21⃗22⃗23⃗]=[cos⁡θ3−sin⁡θ30sin⁡θ3cos⁡θ30001]\bold{C_{3}} = \bold{C_{21}} = \begin{bmatrix} \vec{2_1} & \vec{2_2} & \vec{2_3} \end{bmatrix} = \begin{bmatrix} \begin{array}{c:c:c} \cos{\theta_3} & -\sin{\theta_3} & 0 \\[2ex] \sin{\theta_3} & \cos{\theta_3} & 0 \\[2ex] 0 & 0 & 1 \end{array} \end{bmatrix}

由 C21⋅F1=F2\bold{C_{21}} \cdot \bold{F_1} = \bold{F_2} 可得：

F1↦C21F2\bold{F_1} \xmapsto{\bold{C_{21}}} \bold{F_2}

即：

C21⋅[11⃗12⃗13⃗]=[21⃗22⃗23⃗]\bold{C_{21}} \cdot \begin{bmatrix} \vec{1_1} & \vec{1_2} & \vec{1_3} \end{bmatrix} =\begin{bmatrix} \vec{2_1} & \vec{2_2} & \vec{2_3} \end{bmatrix}

3.2 绕 < 2 - 轴 > 旋转

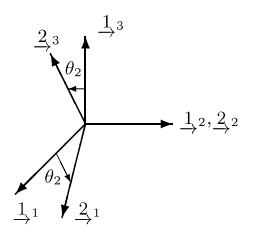
screenShot.png

先将 F1→\underrightarrow{F_1} 看做基向量空间 II ，可推出：

{21⃗T=[cos⁡θ20−sin⁡θ2]22⃗T=[010]23⃗T=[sin⁡θ20cos⁡θ2]\begin{cases} &\vec{2_1}^{T} = \begin{bmatrix} \cos{\theta_2} & 0 & -\sin{\theta_2} \end{bmatrix} \\[2ex] &\vec{2_2}^{T} = \begin{bmatrix} 0 & 1 & 0 \end{bmatrix} \\[2ex] &\vec{2_3}^{T} = \begin{bmatrix} \sin{\theta_2} & 0 & \cos{\theta_2} \end{bmatrix} \end{cases}

可得绕 < 2 - 轴 > 旋转的 旋转矩阵 C2\bold{C_{2}} 为：

C2=C21=[cos⁡θ20sin⁡θ2010−sin⁡θ20cos⁡θ2]\bold{C_{2}} = \bold{C_{21}} = \begin{bmatrix} \begin{array}{c:c:c} \cos{\theta_2} & 0 & \sin{\theta_2} \\[2ex] 0 & 1 & 0 \\[2ex] -\sin{\theta_2} & 0 & \cos{\theta_2} \end{array} \end{bmatrix}

由 C21⋅F1=F2\bold{C_{21}} \cdot \bold{F_1} = \bold{F_2} 可得：

F1↦C21F2\bold{F_1} \xmapsto{\bold{C_{21}}} \bold{F_2}

即：

C21⋅[11⃗12⃗13⃗]=[21⃗22⃗23⃗]\bold{C_{21}} \cdot \begin{bmatrix} \vec{1_1} & \vec{1_2} & \vec{1_3} \end{bmatrix} =\begin{bmatrix} \vec{2_1} & \vec{2_2} & \vec{2_3} \end{bmatrix}

3.3 绕 < 1 - 轴 > 旋转

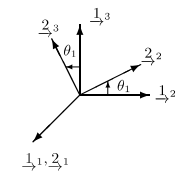
screenShot.png

先将 F1→\underrightarrow{F_1} 看做基向量空间 II ，可推出：

{21⃗T=[100]22⃗T=[0cos⁡θ1sin⁡θ1]23⃗T=[0−sin⁡θ1cos⁡θ1]\begin{cases} &\vec{2_1}^{T} = \begin{bmatrix} 1 & 0 & 0 \end{bmatrix} \\[2ex] &\vec{2_2}^{T} = \begin{bmatrix} 0 & \cos{\theta_1} & \sin{\theta_1} \end{bmatrix} \\[2ex] &\vec{2_3}^{T} = \begin{bmatrix} 0 & -\sin{\theta_1} & \cos{\theta_1} \end{bmatrix} \end{cases}

可得绕 < 1 - 轴 > 旋转的 旋转矩阵 C1\bold{C_{1}} 为：

C1=C12=[1000cos⁡θ1−sin⁡θ10sin⁡θ1cos⁡θ1]\bold{C_{1}} = \bold{C_{12}} = \begin{bmatrix} \begin{array}{c:c:c} 1 & 0 & 0 \\[2ex] 0 & \cos{\theta_1} & -\sin{\theta_1} \\[2ex] 0 & \sin{\theta_1} & \cos{\theta_1} \end{array} \end{bmatrix}

由 C21⋅F1=F2\bold{C_{21}} \cdot \bold{F_1} = \bold{F_2} 可得：

F1↦C21F2\bold{F_1} \xmapsto{\bold{C_{21}}} \bold{F_2}

即：

C21⋅[11⃗12⃗13⃗]=[21⃗22⃗23⃗]\bold{C_{21}} \cdot \begin{bmatrix} \vec{1_1} & \vec{1_2} & \vec{1_3} \end{bmatrix} =\begin{bmatrix} \vec{2_1} & \vec{2_2} & \vec{2_3} \end{bmatrix}